Астрономия шпоры. Небесная сфера. Отвесная линия. Ось мира. Меридиан наблюдателя. Система сферических координат и полярных координат
 Скачать 1.04 Mb. Скачать 1.04 Mb.
|
|
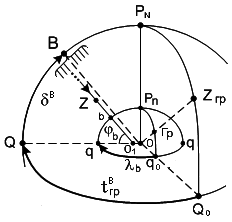
Полюс освещения и его координаты. От светила В на Землю направлен пучок параллельных лучей (рис. 59). От светил солнечной системы непараллельность лучей (параллакс) учитывается при исправлении высот (см. разд. 2.5.1.). Один из лучей совпадает с отвесной линией О1b. Точка b на Земле, в которой светило видно в зените, называется полюсом освещения или географическим местом светила.
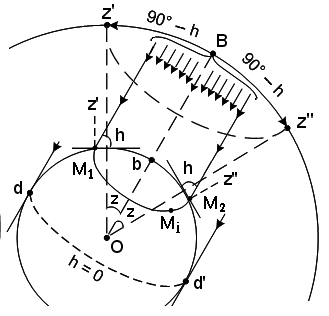
b = В; b = t. (112) Значения В и t выбираются из МАЕ на заданное время Тгр и по ним можно нанести на карту или глобус географическое место светила. Так как с течением времени часовые углы светил непрерывно возрастают, то их полюсы перемещаются по Земле с востока на запад. Круг равных высот (КРВ). На рис. 60 пучок параллельных лучей от светила В попадает на поверхность земного геоида. Наблюдатели на Земле в точках М1, М2 и Мi видят светило В на одной и той же высоте h, следовательно дуга М1 Мi М2 является изолинией высоты h.
Учитывая отклонения отвесной линии и форму Земли, круг равных высот на земной поверхности представляет сложную кривую. На небесной сфере круг равных высот является сферической окружностью Z’Z с центром в точке светила В и радиусом Z = 90° – h. Если Землю принять за шар, то большой круг dd с центром в точке b (полюс освещения) представляет границу освещенности на Земле светилом В (h = 0). Так как высота светила меняется от 90° до 0°, т. е. 5400, а на земном шаре (глобусе) это расстояние равно 5400 миль, то одна минута изменения высоты равна морской миле. На реальной поверхности Земли (геоиде) и на картах меркаторской проекции изолинии высоты представляют сложные кривые, а не сферические окружности.
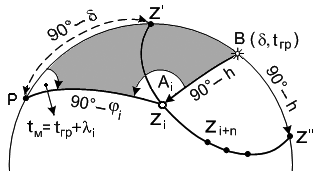
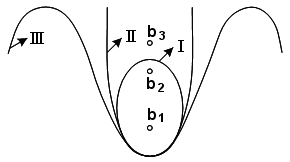
sinh= sinφi sin + cosφi cos cos(tгр + i) (113) Следовательно, , tгр и 90° – h представляют параметры круга равных высот, а i и i – текущие координаты круга равных высот. Круг равных высот на меркаторской карте. На карте в меркаторской проекции круги равных высот и представляют циклические кривые трех типов (рис. 62).
II тип – соответствует кругу равных высот, проходящий через повышенный полюс мира. III тип – соответствует кругу равных высот, включающего повышенный полюс мира. 3.2.3. Высотная линия положения Замена участка круга равных высот около счислимого места прямой линией называется высотной линией положения (ВЛП). 28.32.35. Определение места по Солнцу (разновременные наблюдения) При определении места по Солнцу для получения 2-ой ВЛП необходим промежуток времени, за который азимут Солнца изменится на величину не менее 30°. Поэтому такие наблюдения называются разновременными или кратко «по Солнцу». В основу определения места положен способ «крюс-расстояний». Принцип определения места по Солнцу. Допустим в момент Тс1 (Тгр1) в координатах с1 и с1 (Мс1) была измерена высота Солнца и вычислены элементы первой ВЛП – Ас1 и п1. После изменения азимута Солнца на величину А 30° в момент Тс2 (Тгр2) выполнены 2-ые наблюдения. Так как судно прошло расстояние S в направлении ПУ (К), то счислимые координаты изменились на с2 и с2 (Мс2). Расчетные элементы второй ВЛП будут Ас2 и п2. На рис. 76 выполнена прокладка движения судна и ВЛП из точек Мс1 и Мс2 (линии I-I и II-II). Допустим, что действительное место судна находилось на линии I-I в точке М1. Перенеся эту линию по счислению из точки М1 на расстояние S, получим линию I-I, которая пересекается с линией II-II в точке Мо, так как действительное место судна находится на обеих линиях положения. Аналогично переносится определяющая точка к1 в точку к1. Из рисунка видно такой перенос равноценен прокладке Ас1 и п1 из точки Мс2.
Поэтому, место, полученное по разновременным наблюдениям, является счислимо-обсерврванным. Оценка обсервации выполняется по формуле Последовательность выполнения обсервации по Солнцу. 1. Подготовка к наблюдениям заключается в планировании времени наблюдений, в которых, как правило, задается время получения обсервации. Определение времени первых наблюдений представляет достаточно сложную задачу, в которой должны быть выполнены два условия: промежуток времени между наблюдениями не более 2ч – 2,5ч (ошибки счисления mсч ухудшают надежность 1-ой ВЛП); разность азимутов должна быть не менее 30°. Скорость изменения азимута является общим критерием для нахождения оптимального соотношения этих двух условий. Из анализа изменения азимута (Аt) в суточном движении светил (см. разд. 1.3.2.) следует, что около меридиана наблюдателя Аt наибольшая, а около I-го вертикала – наименьшая. Следовательно, наиболее точное место при определении по Солнцу получают при наблюдениях выполненных до и после момента кульминации (симметрично). Решение может быть выполнено либо по методике изложенной в литературе [2], либо с помощью звездного глобуса [1]. Примечание. Необходимость решения этой задачи возникает при определении места в 1-ой половине дня (на вахте с 08ч до 12ч). Во 2-ой половины дня обычно при выполнении первых наблюдениях измеряют азимут на Солнце или получают его после обработки 1-ой ВЛП. Вторые наблюдения выполняют, когда азимут изменится на величину не менее 30°. Перед выполнением 1-х наблюдений выполняется подготовка секстана (см. раздел 2.4.4.) и определяется поправка индекса секстана. 2. Наблюдения Солнца выполняются с дневной трубой. Сведение края Солнца с горизонтом около кульминации (высота изменяется медленно) производят вращением отсчетного барабана, а далеко от меридиана (высота изменяется быстро) – ожиданием на заранее установленном отсчете. При каждых измерения рекомендуется выполнять 35 измерений с фиксацией моментов с последующим их осреднением. 3. Обработка наблюдений производится по вычислительной схеме приведенной в литературе [1], [2]. Определение места по звездам (одновременные наблюдения) Особенности обсервации при одновременных наблюдениях. 1. Обработка наблюдений (расчет элементов ВЛП) выполняется относительно одного счислимого места (с, с). На ходу судна измерения высот светил происходит из разных мест также как и при обсервации по Солнцу. Для получения измеренных высот как бы из одной точки (с, с) необходимо выполнить приведение высот к одному месту (зениту) аналитическим (см. разд. 2.5.4.) или графическим способом. 2. Обсервация по звездам возможна только утром, вечером и иногда ночью, когда обеспечивается одновременная видимость горизонта и светил. Последовательность выполнения обсервации по звездам. 1. Подготовка к наблюдениям заключается в расчете времени начала наблюдений (см. разд. 1.6.4.) вечером – середина гражданских сумерек по формулам (61) и утром – середина навигационных сумерек по формулам (62). На момент начала наблюдений с помощью звездного глобуса выполняется подбор звезд. Последовательность решения этой задачи с примерами и рисунками изложены в литературе [1], [2]. Перед выполнением наблюдений выполняется подготовка секстана (см. раздел 2.4.4.) и определяется поправка индекса секстана. 2. Наблюдения звезд выполняются с ночной трубой (звезды видны без трубы) и с дневной трубой (звезды не видны без дневной трубы), которая позволяет увеличить время наблюдений в два раза. В случае ночных наблюдениях – без трубы. При каждых измерения рекомендуется выполнять 3 измерения с фиксацией моментов с последующим их осреднением. Примечание. При наблюдении более 3-х светил выполняют только одно измерение. В этом случае появляется возможность анализа ВЛП на промах и исключения этой ВЛП из обсервации. 3. Обработка наблюдений производится по вычислительной схеме приведенной в литературе [1], [2]. Определение места по звездам методом перемещенного места При обработке наблюдений (решение параллактического треугольника) по иностранным численным таблицам, в которых входными аргументами являются °мп и tмп°с целыми градусами, применяется метод перемещенного места. В основе метода лежит 3-е свойство ВЛП.– независимость линии положения от счислимых координат. Перемещение счислимых координат делается в пределах 30. Широту °мп получают обычным округлением ее до целого градуса. Получение tмп° достигается путем изменения с для каждой ВЛП на величину i. Таким образом, прокладка каждой ВЛП выполняется из своей счислимой точки. Нахождение перемещенных мпi можно выполнить 3-я приемами. Прием ввода с + 30Е в расчет tмп° и i позволяет избежать ошибок в вычислениях. В этом приеме величина i всегда W в пределах от 0 до 60 откладываются от меридиана с + 30Е.
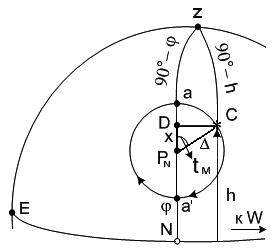
Для решения параллактического треугольника tмп° = 294°. (W) = 2,2 предназначено для нахождения при прокладке на параллели °мп долготы точки, из которой выполняется прокладка данной ВЛП. Обработка наблюдений производится по вычислительной схеме приведенной в литературе [1], [2]. Оценка обсервации. Вследствие того, что переносы при перемещенном месте могут достигать величины до 40, т. е. нарушается 1-е свойство ВЛП, то возникают дополнительные методические ошибки в ВЛП (см. разд. 3.2.5) и оценка места должна выполнятся по формуле Определение широты по меридиональной высоте светила. Выгодным условием определения широты места (см. разд. 3.2.7.) является нахождение светила в момент кульминации на меридиане наблюдателя. В этом случае высота называется меридиональной (Н) и азимут А = 180° (0°). Уравнение круга равных высот примет вид sin H = sin sin + cos cos cos 0° или sin H = cos ( – ). Так как Н = 90° – Z, то sin H = cos Z = cos ( – ) и следовательно Z = – , откуда = Z + .
Значение и наименование широты так же зависит от наименования . Наименования широты и расчетную формулу можно получить при рассмотрении 2-х ситуаций, показанных на рис. 77. 1. Для светила С1 имеем склонение 1N и меридиональную высоту Н1 к S, по которой получим Z1 N, т. е. Z1 одноименно со склонением 1. Из рисунка получим формулу расчета широты = Z1 + 1 () и широта одноименна с Z и . 2. Для светила С2 имеем склонение 2S и меридиональную высоту Н1 к S, по которой получим ZC2= Z2 N, т. е. Z2 разноименно со склонением 2. Из рисунка получим формулу расчета широты = Z2 – 2 () и широта одноименна с большим членом формулы По формулам () и () получим общую формулу расчета широты = Z . (142) При одноименных Z и знак «+» и широта одноименна с ними. При разноименных Z и знак «–» и широта одноименна с большим членом (Z или ) формулы. Рекомендуется получить решение задачи на сфере как на рис. 77. Последовательность решения: 1. Изобразить меридиан наблюдателя, отвесную линию и горизонт. Обозначить точки N и S горизонта. 2. По высоте Н нанести положение светила и наименования точек горизонта. 3. Отложив от светила , получим положение экватора, а затем перпендикулярно ему провести ось мира. 4. По рисунку составить формулу расчета широты. Обычно метод определения широты по Н применяется только для Солнца. Время начала наблюдений определяется как Тснаб = Тск – 5м. Измерение меридиональной высоты выполняется приведением нижнего края отраженного Солнца к касанию с горизонтом с помощью барабана отсчетного устройства до момента уменьшения высоты Солнца. Пример полной обработки наблюдений для определения о приведен в литературе [1]. Здесь приведем только вычислительную схему обработки наблюдений. Расчет кульминации Расчет склонения Расчет широты
Достоинством определение широты места по меридиональной высоте Солнца является не зависимость метода от счислимой широты места (не требуется знания места), а также скорость получения результата. Определение широты по высоте Полярной звезды. Метод получения обсервованной широты места основан на переходе от обсервованной высоты Полярной звезды к широте путем введения 3-х поправок.
Из рис. 78 видно, что для любой точки параллели широта определяется формулой = h х. (143 |


 с + 30Е
с + 30Е