Астрономия шпоры. Небесная сфера. Отвесная линия. Ось мира. Меридиан наблюдателя. Система сферических координат и полярных координат

• Название: Небесная сфера. Отвесная линия. Ось мира. Меридиан наблюдателя. Система сферических координат и полярных координат
• Анкор: Астрономия шпоры.doc
• Дата: 12.10.2017
• Размер: 1.04 Mb.
• Имя файла: Астрономия шпоры.doc
• Тип: Документы; #9305
• страница: 6 из 7

2.5.5. Измерение высот светил

Измерение высот светил является трудоемкой операцией, которую можно условно разделить на три этапа: приведение светила к горизонту, отыскание вертикала светила; совмещение края Солнца или центра звезды с видимым горизонтом.

Эти этапы могут выполняться различными способами, методика которых подробно рассмотрены в литературе [1, 3, 4].

Освоение процесса измерения высот светил достигается только длительной тренировкой. Такую тренировку лучше выполнять при стоянке в порту или на якорной стоянке, где есть открытый видимый горизонт.
24. 25 .Опр попр компаса

ОПРЕДЕЛЕНИЕ ПОПРАВКИ КОМПАСА

Основы астрономического определения поправки компаса

Единственным способом определения поправки компаса К в открытом море является астрономический. Кроме того этот способ обеспечивает наибольшую точность получения К при условии использования точных координат судна, например при стоянке в порту.

К = ИП^св – КП^св (98)

В отличии от навигационных способов истинный пеленг на светило вычисляется как азимуту светила в круговом счете при решении параллактического треугольника.

В зависимости от заданных аргументов в настоящее время используют три метода вычисления азимута на светило (см. разд. 1.2.1.).

Метод моментов. В этом методе заданы аргументы _м, ^св и tсвм, т. е. А = f(, , t) и азимут вычисляется по формуле (4)

ctgA =tg cosφ cosect_м – sinφ ctgt_м (99)

Этот метод универсален – его применяют при любых условиях и он является основой общего способа определения поправки компаса.

Метод высот. В этом методе заданы аргументы _м, ^св и h^св т. е. А= f(, , t) и азимут вычисляется по формуле (5)




(100)

Этот метод применяется в основном в частых случаях, когда известна высота светила, например при восходе (заходе) Солнца.

Метод высот и моментов. В этом методе заданы аргументы _м, h^св и tсвм т. е. А= f(, h, t) и азимут вычисляется по формуле (6)

sinA = sin cost_м sесh (101)

Этот метод применяется при одновременном определении места судна (при измерении высот) и поправки компаса, а так же в частном случае при определении К по Полярной звезде.

Постоянная поправка гирокомпаса определяется как средняя по серии отдельных (мгновенных) поправок по формуле

, (102)

где ГК_i = ИПсвi – ГКПсвi – мгновенная поправка гирокомпаса;

N – число поправок.

Влияние погрешности в счислимых координатах судна на

истинный пеленг светила

Так как в формулах (99101) в основном используются счислимые координаты судна – _с и _с, то и азимут светила получают счислимый А_с, а не истинный А_и. Другими словами, погрешности в координатах судна  и  трансформируются в погрешности в азимуте по широте и долготе, которые можно представить в виде ряда

(103)

Продифференцировав формулу (99) по λ и  и выполнив ее преобразование, получим формулу расчета значения поправки А_

А_ = tgh sinA  (104)

Формула (27) изменения азимута светила в суточном движении получена в разд. 1.3.2. в виде

A_t = –( sinφ – tgh cosA cosφ) t.

Так как t_м = t_гр   и значение t_гр безошибочно (связано только с моментом измерения), то t =  . Другими словами, погрешность в часовом угле светила вызывается погрешностью в счислимой долготе.

После замены переменной получим формулу расчета A_

A_ = ( sinφ – tgh cosA cosφ)  (105)

Для анализа погрешности А в счислимом азимуте выразим  и  в формулах (104, 105) через невязку С (снос) и направление невязки С^сн и после преобразований получим следующую формулу

А = А_ + А_ = Сtgh sinA cosC^сн – C (sin – cos tgh cosA) sinС^сн sec.

Основными аргументами влияющих на величину А являются значения невязки С и высоты светила h.

Вычисления по этой формуле при невязке С  10 миль и высоте светила h 18° дали следующие результаты: в малых широтах А  0,1°; в широтах до 60° А  0,25°; в широтах до 70°  75° А  0,4°.

На основе приведенного анализа получим следующие выводы:

• 
  чем меньше высота h, тем меньше погрешность А;
  
• 
  принимаем ИПсви = ИПсвс в широтах до 60° и h 18° при С  10 миль, а широтах свыше 60° при С  3 миль;
  
• 
  в малых северных широтах для определения К рекомендуется выполнять по Полярной звезде, так как ее азимут практически не изменяется в течении 20^м30^м , т. е. мало зависит от счислимых координат.
  

Частные способы определения поправки компаса

Частные способы упрощают получение истинного пеленга на светило. Эти способы применимы только для Солнца в момент видимого восхода (захода) и Полярной звезды.

Примечание. Применение общего способа определения К в этих случаях дает более точный результат особенно для Солнца.

Поправка компаса по азимуту видимого восхода (захода) Солнца. Явление видимого восхода (захода) Солнца рассмотрено в разделе 1.6.4.

Рис. 53

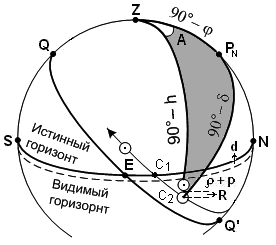
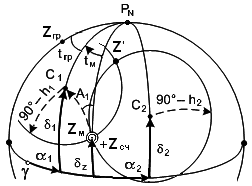
Высоту центра Солнца в момент видимого восхода (захода) (рис. 53) получим по формуле (54)

h^= – d–  +p – R^,

где где d– наклонение видимого горизонта;  – астрономическая рефракция;
р – параллакс Солнца; R^ – видимый радиус Солнца.

Азимут видимого восхода (захода) Солнца получим по аргументам ,  и h параллактического ZP_NC₂ по формуле (100) метода высот, полученной в разделе 3.1.1.



По этой формуле вычислены азимуты (в круговом счете), приведенные в ежедневных таблицах МАЕ на каждую дату года.

Аргумент высоты Солнца h^= –50,3 = const. с учетом высоты глаза наблюдателя е = 0 метров (d = 0), стандартной астрономической рефракции и параллакса ( + p = –34,3), радиуса Солнца (R^ = –16).

Аргумент  Солнца вычислен на момент восхода (захода) каждых суток на Гринвичском меридиане.

Аргумент широты места задан в виде табличных широт от 74°N до 60°S.

Таким образом, получение азимута выполняется по дате и координате широты места судна по формуле

А_с = А_т + А_ + А_, (106)

где А_ – интерполяция по широте места;

А_ – интерполяция по долготе места.

Действительная высота отличается от табличной (h^= –50,3) за счет наклонения видимого горизонта d и поправок высоты за температуру и давления атмосферы, которые выбираются из таблиц исправления высот (разд. 2.5.1.), на величину h_д

h_д = d + h_t + h_B (107)

Дополнительная поправка азимута А_д вычисляется по формуле

А_д = –0,0017 tg h_д cosecA (108)

Достоинством этого способа простота и скорость вычисления А_с, а так же процесс измерения пеленга не отличается от навигационных измерений.

Недостатками являются:

• 
  меньшая точность в ГКП за счет только одного измерения;
  
• 
  способ применим два раза в сутки при условии безоблачного неба в районе восхода (захода);
  
• 
  появление больших погрешностей в А_с за счет аномального состояния атмосферы в приполярных районах, в которых астрономическая рефракция достигает 1°2°.
  

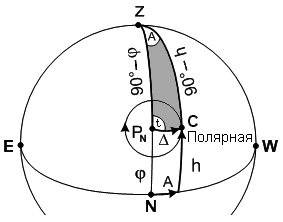
Поправка компаса по Полярной звезде. Движение Полярной звезды происходит по суточной параллели с радиусом равным полярному расстоянию   43 (рис. 54).

Рис. 54

Вследствие малого сферического радиуса параллели азимут Полярной звезды в широтах до 35°N изменяется всего от 0° до 1° NE и NW. Поэтому для вычисления азимута можно применить формулу (101) метода высот и моментов. Из параллактического ZCP_N получим

sinA = sin sint_м sесh

и учитывая, что t_м = S_м +  и небольшие значения элементов A и  равны их синусам, а так же примем  = h получим расчетную формулу азимута Полярной звезды

A =  sec sin(S_м +) (109)

По этой формуле, принимая средние значения за год  и , вычислена таблица в МАЕ «Азимут Полярной» с точностью до 1. Аргументами для входа в таблицу являются широта места  и звездное местное время S_м.

К достоинствами этого способа следует отнести:

• 
  простота и скорость обработки наблюдений;
  
• 
  медленное изменение азимута особенно в малых широтах. Азимут практически не изменяется в течении 10  20 минут.
  

Недостатком является практическое ограничение применения способа по широте места от 10°N до 35°N.

Пеленгование светил. Точность поправки компаса

Выполнение пеленгования. Для пеленгования подбирают светила с наименьшей высотой (см. разд. 3.1.2.) в пределах до 35° при прямовидимом пеленговании и наименьшей скорости изменения азимута, т. е. около I-го вертикала (см. выводы изменения азимута в разд. 1.3.2.)

Рис. 55

Пеленгование выполняют одновременным совмещением на нити пеленгатора центра светила и пузырька уровня (рис. 55).

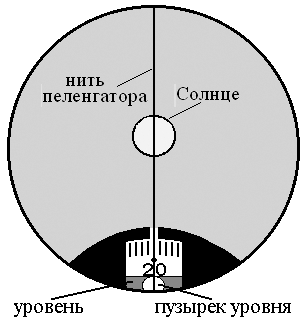
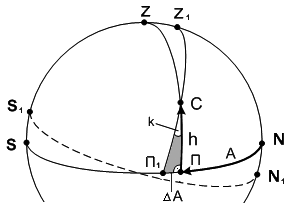
Снятие ГКП и момента Т производят после нескольких «прицеливаний», пока не получится устойчивый результат или выполняют три измерения ГКП и Т с последующим их осреднением.

Процесс одновременного совмещения светила и пузырька уровня требует большой тренировки на ходу судна и особенно при качке.

Погрешность компасного пеленга. Погрешность в ГКП складывается из погрешностей гирокомпаса и погрешностей измерения пеленга.

Погрешность измерения пеленга возникает в основном от наклона плоскости пеленгования к истинному горизонту (рис. 56).

Рис. 56

Положению Z₁ соответствует истинный горизонт S₁N₁ (пунктирная линия) и вертикал светила Z₁СП₁. Дуга ZZ₁ равна углу k наклона плоскости пеленгования. Погрешность измерения А определяется из CПП₁ по формуле

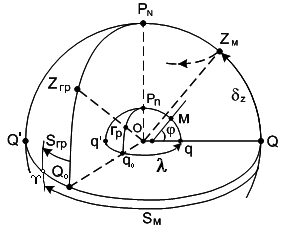
А = k tgh (110)

При удержании пеленгатора в вертикале светила по уровню на ходу судна k  0,5° и при высотах до 20° погрешность оценивается величиной m_КП = 0,3° [2].

Погрешность гирокомпаса (центральный прибор + репитер) в среднем принимается равной m_ГК=0,5° [2].

Погрешность ГКП относительно истинного меридиана m_ГКП = 0,6°.

Если полученная на ходу судна К = 0,5°, то ее принимают равной 0°.

26.27. Основы астр ОМС.

Задача определения места сводится к определению положения зенита относительно мест светил (ориентиров) на небесной сфере с переходом обратно на поверхность Земли.

Примечание. Решение задачи непосредственно на поверхности Земли (геоиде) значительно сложнее по сравнению с решением на сфере.

Связь места судна и положением его зенита. Географические координаты  и  точки М и небесные координаты его зенита _z и t связаны соотношениями вытекающими из рис. 57.

Рис. 57

По построению (переносу отвесной линии в точке М на Земле в центр О)  = _z. Долгота места  равна дуге небесной сферы QQ, которую можно получить как разность

S_м – S_гр или на основании основной формулы времени как tсвм – tсвгр, т. е.


(111)
= _z;

 = S_м – S_гр = tсвм – tсвгр.

Вследствие суточного вращения сферы место зенита непрерывно перемещается по параллели, поэтому по формулам (111) получаем мгновенное место на момент Т_гр измерения высоты.

Принципы определения места зенита. Для определения мгновенного места зенита (места судна) необходимо иметь данные измерений о его расположении относительно мест двух светил (рис. 58). В навигации, измеряемые физические величины U, являющиеся функциями координат  и , называются навигационными параметрами [5].

Для светил может быть 8 таких параметров, однако в настоящее время на транспортном флоте применяется только параметр высоты. Весь процесс измерений и их обработки называют астрономической обсервацией.

Обработка наблюдений, т. е. определение обсервованного места, может выполняться различными методами [1, 2]. В настоящее время в основном используется графоаналитический метод (метод линий положения см. разд. 3.2.3.).

Графический метод, основанный на принципе навигационных изолиний, позволяет пояснить принцип и особенности астрономической обсервации.

Рис. 58

На рис. 58 показана обсервация по двум измеренным высотам светил С₁ и С₂, выполненная графическим способом на небесной сфере.

Последовательность выполнения решения обсервации по измерениям высот двух светил следующая:

• 
  нанести на сферу положение светил С₁ и С₂ по координатам  и ;
  
• 
  проведя изолинии параметров измеренных высот (сферические круги радиусом равным Z_i = 90° – h_i), получим места двух зенитов;
  
• 
  действительное место зенита наблюдателя (Z_м) определяется по дополнительной информации либо по зениту счислимого места (Z_сч), нанесенного на сферу (координаты S_сч = S_гр   и _z = _сч), либо по измеренному азимуту на любое светило (А₁);
  
• 
  снять координаты точки зенита Z_м (S_м и _z) и по формулам (111) получить обсервованные географические координаты судна.
  

Кроме рассмотренных методов при решении астрономических задач на компьютере используется итерационный обобщенный метод наименьших квадратов, рассмотренный в курсе «Математические основы судовождения» [5].

Астрономические изолинии. Круг равных высот

Навигационные параметры U на сфере, земном геоиде и карте представлены в виде изолиний, т. е. геометрическим местом точек равных значений навигационного параметра. Каждая изолиния описывается своим уравнением U = f(, ). В таблице 2 приведены 3 из 8 изолиний.

Таблиц 2

№ п/п	Навигационный параметр	Название изолинии
1	Высота (h)	Круг равных высот (сферическая окружность)
2	Разность высот (h)	Сферическая гипербола
3	Азимут (А)	Изоазимута

Фундаментальное отличие астрономических изолиний от земных изолиний заключается в том, что навигационные ориентиры (светила) находятся на небесной сфере и их координаты непрерывно изменяются вследствие суточного вращения Земли (по времени). Координаты земных ориентиров не изменяются. Рассмотрим подробно изолинию высоты.