Астрономия шпоры. Небесная сфера. Отвесная линия. Ось мира. Меридиан наблюдателя. Система сферических координат и полярных координат
 Скачать 1.04 Mb. Скачать 1.04 Mb.
|
|
Эклиптическая система координат Основным направлением является ось эклиптики. Основными кругами являются: эклиптика и круг широты точки Овна. Вспомогательным кругом является круг широт. Кругом широт называется половина большого круга, проходящего через полюса эклиптики и светило. Координаты – эклиптическая широта и эклиптическая долгота. Эклиптической широтой (β) называется дуга круга широт от эклиптики до места светила в пределах от 0° до 90° со знаком «+» к северу и «–» к югу. Эклиптической долготой (λэ) называется дуга эклиптики от точки Овна до круга широты светила в пределах от 0° до 360° в сторону счета координаты прямого восхождения (). Долгота Солнца в характерные даты совпадает с его значениями прямого восхождения, т.е. 0°; 90°; 180°; 270°. 8.Приближенное решение задач на годовое и суточное движение Солнца.  Рис. 13 Связь координат Солнца и с его долготой λэ. Рассмотрим сферический прямоугольный С2D, в котором заданы элементы ε и λ.э Для нахождения стороны D = применим формулу косинуса стороны, а для нахождения стороны С2D = применим формулу синусов получим c  (29) ) (30) os = cosλэ / cos sin = sinλэ sinε Суточные изменения координат Солнца. Как указывалось выше, скорость движения Солнца по эклиптике неравномерна. Суточная скорость изменения долготы Солнца: в перигелии (точка П рис. 12) λэ= 61,2/д; в афелии (точка А) λэ= =57,2/д; в среднем λ= 59,14/д. Для получения формул расчета и следует продифференцировать формулы (30) и перейти к конечным приращениям. При расчете с данными основных точек эклиптики получим: меняется от 54/д до 66,6/д; – от 0 до 24/д; наибольшее значение =66,6/д Солнце имеет около 22 декабря (самые длинные сутки); наименьшее значение =53,8/д Солнце имеет около 18 сентября (самые короткие сутки); среднее значение за год =59,14/д. Приближенный расчет координат Солнца на любую дату в году выполняется с помощью графика (рис. 14) относительно ближайшей основной даты (табл. 1) по следующим правилам:
= 0,1°/д в течении 30 дней до и после дней солнцестояний; = 0,3°/д в течении 2-го месяца после основных дат. = 1°/д в течении года. 9. Орбитальное движение Луны измен-е экватор-х коорд. Луны . Как известно орбита Земли является орбитой центра тяжести (ЦТ) системы Земля–Луна (рис. 15), который находится под поверхностью Земли. Если рассматривать систему Земля–Луна независимо от солнечной системы (как задачу двух тел), то орбита Луны характеризуется законами Кеплера, т. е. это эллипс, в одном из фокусов которого находится центр тяжести системы. Изменение сил притяжения Солнца и планет на координаты Луны учитываются как возмущения.
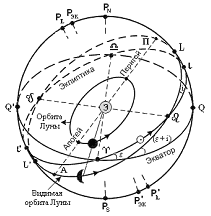
Средняя орбитальная скорость Луны υ =1,02 км/сек. Видимая орбита Луны. На рис. 16 изображена геоцентрическая небесная сфера. Плоскость орбиты Луны в пересечении с небесной сферой даст большой круг (LL), называемый видимой орбитой Луны. Перенесем на небесную сферу экватор (QQ) и эклиптику (ll). Видимая орбита Луны пересекается с эклиптикой под углом i ≈ 5°09 в двух точках называемых узлами: восходящий узел ( Под воздействием сил тяготения Солнца и планет возникают возмущения, вследствие которых элементы эллипса непрерывно изменяются. Наибольшие члены возмущений называются эвекция и вариация. Их действия вызывают следующие явления:
Изменение координат и Луны. Координаты Луны быстро и непрерывно меняются. Среднее суточное изменение = 13,2° и изменяется в пределах от 10° до 17° в сутки. Склонение Луны изменяется от 0° до относительного максимума. Относительный максимум изменяется от наибольшего склонения (восходящий узел совпадает с точкой Овна) = ε + i= =23°27 + 5°09= 28°36 N или S до наименьшего склонения =ε–i= 23°27 – 5°09= 28°36 N или S. Суточное изменение склонения меняется от 0,3° до 7° Месячные периоды в движении Луны. Полный оборот Луны по сфере относительно, какой либо точки происходит за месяц. В астрономии различают пять различных месяцев, из которых в мореходной астрономии используют два. Звездным или сидерическим месяцем называется период оборота Луны относительно какой либо звезды. Средняя продолжительность равна 360° / 13,2° ≈27,32д . Лунным или синодическим месяцем называется период оборота Луны относительно Солнца. За счет собственного годового движения Солнце сместится относительно звезды в ту же сторону, что и Луна (рис. 16) на ≈27,8°. Поэтому полный оборот Луны относительно Солнца будет длиннее звездного месяца на 27,8°/13,2°≈2,11д и лунный месяц равен 29,53д. 12 лунных месяцев или «лунный год» на 11 суток короче тропического и календарного года, т. е. его продолжительность около 354 дней. Фазы и возраст Луны
Луна светит отраженным солнечным светом. Поэтому при ее месячном движении вокруг Земли видимая часть диска Луны непрерывно изменяется и называется сменой фаз. Граница освещенности называется терминатором; видимый край диска Луны называется лимбом. Величина фазы (Ф) характеризуется отношением освещенной части диаметра Луны к ее полному диаметру, т. е. изменяется от 0 до 1. Возрастом Луны(В) называется число дней и их долей пошедших с момента новолунья до данного момента в пределах от 0 до 29,5д. Четыре фазы Луны имеют собственные названия (рис. 18):
В теории приливов рассматриваются периоды, связанные с положениями I – IV. Период 1,5 дня до и после моментов новолунья или полнолунья называется сизигией. Период 1,5 дня до и после моментов первой или последней четвертью называется квадратурой. 10.Навигационные планеты, орбитальное и видимое движение планет . Законы Кеплера. Движение планет и Луны происходит по эллиптическим орбитам и в первом приближении (учитывается только сила тяготения двух тел) характеризуется законами Кеплера (рис. 11).
Из закона следует, что расстояние r обращающего тела в точке П наименьшее, а точке А – наибольшее. Положение обращающего тела на орбите задается радиус-вектором r. Второй закон. Площади, описываемые радиус-вектором в равные промежутки времени, равны рис. 11. Из закона следует, что скорость движения планеты на орбите неравномерная, ближе к Солнцу – быстрее, дальше – медленнее. Третий закон. Квадраты звездных периодов обращения планет вокруг Солнца относятся как кубы больших полуосей их орбит. Из закона следует, что планеты расположенные ближе к Солнцу имеют большую среднюю скорость на орбите: например для Меркурия – υ=48 км/cек, Земли – υ=30 км/cек, Венеры – υ=35 км/cек. . Движение Земли по орбите и видимое годовое движение Солнца
В соответствии 1-ым и 2-ым законами Кеплера с наибольшей скоростью υ =30,3 км/сек Земля движется в точке П– перигелии, который она проходит около 4 января. В противоположной точке А – афелии скорость наименьшая υ = =29,2 км/сек, которую она проходит около 4 июля. Рассмотрим как изменяется место Солнца на сфере в течении года (оборот Земли вокруг Солнца) и связанные с этим явления на Земле. Проекцию орбиты Земли на небесную сферу (видимое с Земли положение Солнца на сфере) называют видимым годовым движением Солнца. 11. Периодические процессы и основные измерения времени. Все материальные тела окружающего нас мира находятся в непрерывном движении. Любое движение означает перемещение (изменение координат) материального тела в пространстве. С другой стороны движение характеризуется реально существующим понятием промежутка времени, за который происходит перемещение материального тела в пространстве, т.е. время является объективным фактором (формой) существования окружающего нас материального мира. Для измерения времени необходимо определить единицы измерений подобно измерениям других физических величин. Так как время является необратимым непрерывным процессом, то для его измерения должны использоваться непрерывные физические периодические процессы. Естественными периодическими процессами, связанные с биологической жизнью на Земле, являются период обращения Земли вокруг Солнца (тропический год) и период вращения Земли вокруг своей оси (сутки). Эти периоды являются основой измерения времени. Промежуток времени между двумя последовательными одноименными кульминации светила (точки) на небесной сфере на одном и том же меридиане места называется сутками. В зависимости от того, относительно какой точки измеряется промежуток времени, получают звездное (–точка Овна), истинное солнечное (–истинное Солнце) и среднее солнечное (–среднее Солнце) время. Так как продолжительность истинных солнечных суток в течении года изменяется (2-ой закон Кеплера ), то часы, минуты и секунды также изменяют свою длительность. С целью получения постоянных единиц измерения времени введено понятия среднего Солнца. Основной единицы измерения времени является секунда как соответствующая доля тропического года, для воспроизведения которой используются различные непрерывные физические периодические процессы (механический маятник, частота колебаний кварца и т.д.). В настоящее время (с 1967 г.) эталоном единицы измерения времени является атомная секунда определяемой частотой излучения молекул и атомов, так как эти частоты имеют наиболее стабильную величину: «секунда – это 9 192 631 770 периодов излучения, соответствующего резонансной частоте перехода между двумя сверхтонкими уровнями основного состояния атома цезия 133». Для предвычисления видимых координат светил для астрономических ежегодников с 1986 г. используется равномерная шкала земного динамического времени вместо эфемеридного времени, в которой секунда определена как соответствующая доля тропического года. Системы счета времени определяются меридианом, от которого ведется счет:
Промежутки времени можно выражать во временной и угловой мере градусах или радианах. Большие промежутки времени измеряются календарными годами (оборот Солнца), месяцами (оборот Луны) и неделями (искусственное образование). 12.Звездное время. Ед измер. Осн. формула времени. Звездное время. Основная формула времени При рассмотрении вращения небесной сферы относительно точки Овна получим систему счета звездного времени (рис. 22). Промежуток времени между двумя последовательными верхними кульминациями точки Овна на одном и том же меридиане места называется звездными сутками. Звездным временем(S) называется промежуток времени в звездных единицах от верхней кульминации точки Овна до данного момента (положения точки Овна). Так как звездные сутки короче солнечных суток (см. разд. 2.5. рис. 16), то единицами звездного времени являются звездные часы, минуты, секунды. Начало звездных суток в течении года приходится на разное время солнечных суток и поэтому звездное время даты не имеет. Звездное время используется при работе со звездным глобусом или звездной картой и обработке наблюдений звезд (расчет местных часовых углов звезд), при которых его выражают в градусной мере. Основная формула времени. Так как время не зависит от широты места, то вопросы, связанные с измерением времени, удобно иллюстрировать рисунками в виде проекции небесной сферы на плоскость небесного экватора. На рис. 22 показаны следующие элементы:
Стрелка (к W) указывает направление вращения небесной сферы (меридианов светил и точки Овна) относительно неподвижного меридиана наблюдателя QQ, т.е. изменение положения меридианов светил, и точки Овна по времени. Рисунок иллюстрирует основную формулу времени, которая связывает первую и вторую экваториальные системы координат и используется для расчета часовых углов светил. Звездное время в данный момент равно сумме вестовых часовых углов светил и их прямых восхождений. Sм = tм* + * = tм + = tм + =… (33) В практических расчетах часовых углов звезд вместо координаты * используется координата звездного дополнения * для замены операции вычитания на сложение tм* = Sм– * = Sм+ * Уравнением времени называется разность среднего и истинного солнечного времени. Числено оно определяется соотношениями (рис. 23) = Т– Т = t – t = – (36) |