интеграл от ирраци функции. Интеграл от иррациональной функции. Непосредственное интегрирование
 Скачать 0.56 Mb.
|
|
Пример.  Т.к. ( , то  Приводя к общему знаменателю и приравнивая соответствующие числители, получаем: 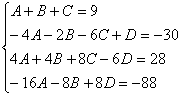 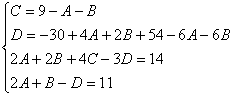 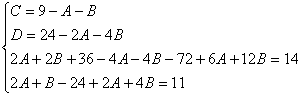 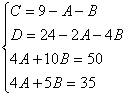 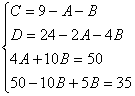 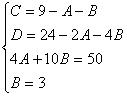   Итого: 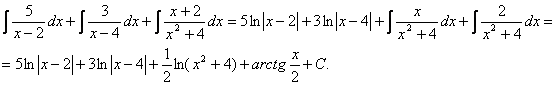 Пример.  Т.к. дробь неправильная, то предварительно следует выделить у нее целую часть: 6x5 – 8x4 – 25x3 + 20x2 – 76x – 7 3x3 – 4x2 – 17x + 6 6x5 – 8x4 – 34x3 + 12x2 2x2 + 3 9x3 + 8x2 – 76x - 7 9x3 – 12x2 – 51x +18 20x2 – 25x – 25 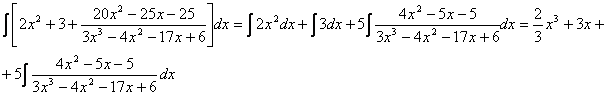 Разложим знаменатель полученной дроби на множители. Видно, что при х = 3 знаменатель дроби превращается в ноль. Тогда: 3x3 – 4x2 – 17x + 6 x - 3 3x3 – 9x2 3x2 + 5x - 2 5x2 – 17x 5x2 – 15x - 2x + 6 -2x + 6 0 Таким образом 3x3 – 4x2 – 17x + 6 = (x – 3)(3x2 + 5x – 2) = (x – 3)(x + 2 )(3x – 1). Тогда:   Для того, чтобы избежать при нахождении неопределенных коэффициентов раскрытия скобок, группировки и решения системы уравнений (которая в некоторых случаях может оказаться достаточно большой) применяют так называемый метод произвольных значений. Суть метода состоит в том, что в полученное выше выражение подставляются поочередно несколько (по числу неопределенных коэффициентов) произвольных значений х. Для упрощения вычислений принято в качестве произвольных значений принимать точки, при которых знаменатель дроби равен нулю, т.е. в нашем случае – 3, -2, 1/3. Получаем: Окончательно получаем: =   Пример.  Найдем неопределенные коэффициенты: 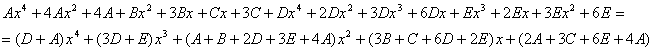 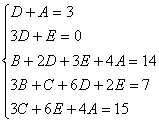 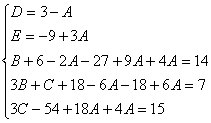 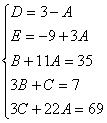 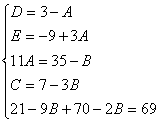  Тогда значение заданного интеграла: 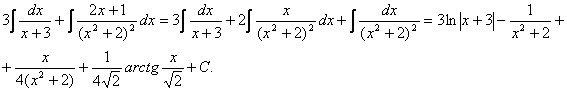 Пример 1 Найти неопределенный интеграл.  Шаг 1. Первое, что мы ВСЕГДА делаем при решении интеграла от дробно-рациональной функции – это выясняем следующий вопрос: является ли дробь правильной? Данный шаг выполняется устно, и сейчас я объясню как: Сначала смотрим на числитель и выясняем старшую степень многочлена: 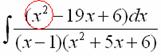 Старшая степень числителя равна двум. Теперь смотрим на знаменатель и выясняем старшую степень знаменателя. Напрашивающийся путь – это раскрыть скобки и привести подобные слагаемые, но можно поступить проще, в каждой скобке находим старшую степень 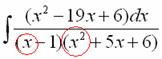 и мысленно умножаем: – таким образом, старшая степень знаменателя равна трём. Совершенно очевидно, что если реально раскрыть скобки, то мы не получим степени, больше трёх. Вывод: Старшая степень числителя СТРОГО меньше старшей степени знаменателя, значит, дробь является правильной. Если бы в данном примере в числителе находился многочлен 3, 4, 5 и т.д. степени, то дробь была бы неправильной. Сейчас мы будем рассматривать только правильные дробно-рациональные функции. Случай, когда степень числителя больше либо равна степени знаменателя, разберём в конце урока. Шаг 2. Разложим знаменатель на множители. Смотрим на наш знаменатель: Вообще говоря, здесь уже произведение множителей, но, тем не менее, задаемся вопросом: нельзя ли что-нибудь разложить еще? Объектом пыток, несомненно, выступит квадратный трехчлен. Решаем квадратное уравнение: Дискриминант больше нуля, значит, трехчлен действительно раскладывается на множители: 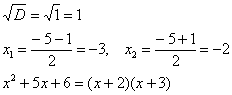 Общее правило: ВСЁ, что в знаменателе МОЖНО разложить на множители – раскладываем на множители. Начинаем оформлять решение:  Шаг 3. Методом неопределенных коэффициентов раскладываем подынтегральную функцию в сумму простых (элементарных) дробей. Сейчас будет понятнее. Смотрим на нашу подынтегральную функцию: И, знаете, как-то проскакивает интуитивная мысль, что неплохо бы нашу большую дробь превратить в несколько маленьких. Например, вот так:  Возникает вопрос, а можно ли вообще так сделать? Вздохнем с облегчением, соответствующая теорема математического анализа утверждает – МОЖНО. Такое разложение существует и единственно. Только есть одна загвоздочка, коэффициенты мы пока не знаем, отсюда и название – метод неопределенных коэффициентов. Как вы догадались, последующие телодвижения Будьте внимательны, подробно объясняю один раз! Итак, начинаем плясать от: В левой части приводим выражение к общему знаменателю:  Теперь благополучно избавляемся от знаменателей (т.к. они одинаковы):  В левой части раскрываем скобки, неизвестные коэффициенты при этом пока не трогаем:  Заодно повторяем школьное правило умножение многочленов. В свою бытность учителем, я научился выговаривать это правило с каменным лицом: Для того чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена. С точки зрения понятного объяснения коэффициенты лучше внести в скобки (хотя лично я никогда этого не делаю в целях экономии времени):  Составляем систему линейных уравнений. Сначала разыскиваем старшие степени: 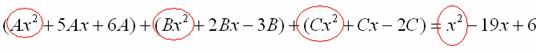 И записываем соответствующие коэффициенты в первое уравнение системы: Хорошо запомните следующий нюанс. Что было бы, если б в правой части вообще не было ? Скажем, красовалось бы просто без всякого квадрата? В этом случае в уравнении системы нужно было бы поставить справа ноль: . Почему ноль? А потому-что в правой части всегда можно приписать этот самый квадрат с нулём: . Если в правой части отсутствует какие-нибудь переменные или (и) свободный член, то в правых частях соответствующих уравнений системы ставим нули. Далее процесс идет по снижающейся траектории, от водки к пиву, отмечаем все «иксы»:  Записываем соответствующие коэффициенты во второе уравнение системы: И, наконец, минералка, подбираем свободные члены. Эх,…что-то я расшутился. Шутки прочь – математика наука серьезная. У нас в институтской группе никто не смеялся, когда доцент на лекции сказала, что разбросает члены по координатной прямой и выберет из них самые большие. Настраиваемся на серьезный лад. Хотя… кто доживет до конца этого урока, все равно будет тихо улыбаться.  Система готова: 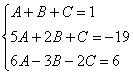 Решаем систему: 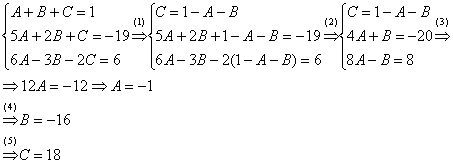 (1) Из первого уравнения выражаем и подставляем его во 2-ое и 3-е уравнения системы. На самом деле можно было выразить (или другую букву) из другого уравнения, но в данном случае выгодно выразить именно из 1-го уравнения, поскольку там самые маленькие коэффициенты. (2) Приводим подобные слагаемые во 2-ом и 3-м уравнениях. (3) Почленно складываем 2-ое и 3-е уравнение, при этом, получая равенство , из которого следует, что (4) Подставляем во второе (или третье) уравнение, откуда находим, что (5) Подставляем и в первое уравнение, получая . Если возникли трудности с методами решения системы отработайте их на уроке Как решить систему линейных уравнений? После решения системы всегда полезно сделать проверку – подставить найденные значения в каждое уравнение системы, в результате всё должно «сойтись». Почти приехали. Коэффициенты найдены, при этом:  Чистовое оформление задание должно выглядеть примерно так:  Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей: 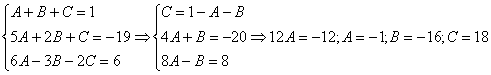  Как видите, основная трудность задания состояла в том, чтобы составить (правильно!) и решить (правильно!) систему линейных уравнений. А на завершающем этапе всё не так сложно: используем свойства линейности неопределенного интеграла и интегрируем. Обращаю внимание, что под каждым из трёх интегралов у нас «халявная» сложная функция, об особенностях ее интегрирования я рассказал на уроке Метод замены переменной в неопределенном интеграле. Проверка: Дифференцируем ответ: 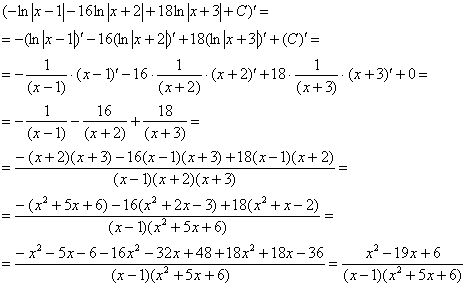 Получена исходная подынтегральная функция, значит, интеграл найдем правильно. В ходе проверки пришлось приводить выражение к общему знаменателю, и это не случайно. Метод неопределенных коэффициентов и приведение выражения к общему знаменателю – это взаимно обратные действия. Пример 2 Найти неопределенный интеграл. Это пример для самостоятельного решения. Полное решение и ответ в конце урока. Вернемся к дроби из первого примера: . Нетрудно заметить, что в знаменателе все множители РАЗНЫЕ. Возникает вопрос, а что делать, если дана, например, такая дробь:  ? Здесь в знаменателе у нас степени, или, по-математически кратные множители. Кроме того, есть неразложимый на множители квадратный трехчлен (легко убедиться, что дискриминант уравнения отрицателен, поэтому на множители трехчлен никак не разложить). Что делать? Разложение в сумму элементарных дробей будет выглядеть наподобие с неизвестными коэффициентами вверху или как-то по-другому?Пример 3 Представить функцию в виде суммы элементарных дробей с неизвестными коэффициентами.Шаг 1. Проверяем, правильная ли у нас дробь Старшая степень числителя: 2 Старшая степень знаменателя: 8 , значит, дробь является правильной. Шаг 2. Можно ли что-нибудь разложить в знаменателе на множители? Очевидно, что нет, всё уже разложено. Квадратный трехчлен не раскладывается в произведение по указанным выше причинам. Гуд. Работы меньше. Шаг 3. Представим дробно-рациональную функцию в виде суммы элементарных дробей. В данном случае, разложение имеет следующий вид:  Смотрим на наш знаменатель: При разложении дробно-рациональной функции в сумму элементарных дробей можно выделить три принципиальных момента: 1) Если в знаменателе находится «одинокий» множитель в первой степени (в нашем случае ), то вверху ставим неопределенный коэффициент (в нашем случае ). Примеры №1,2 состояли только из таких «одиноких» множителей. 2) Если в знаменателе есть кратный множитель , то раскладывать нужно так: – то есть последовательно перебрать все степени «икса» от первой до энной степени. В нашем примере два кратных множителя: и , еще раз взгляните на приведенное мной разложение и убедитесь, что они разложены именно по этому правилу. 3) Если в знаменателе находится неразложимый многочлен второй степени (в нашем случае ), то при разложении в числителе нужно записать линейную функцию с неопределенными коэффициентами (в нашем случае с неопределенными коэффициентами и ). На самом деле, есть еще 4-ый случай, но о нём я умолчу, поскольку на практике он встречается крайне редко. Пример 4 Представить функцию в виде суммы элементарных дробей с неизвестными коэффициентами. Это пример для самостоятельного решения. Полное решение и ответ в конце урока. |