интеграл от ирраци функции. Интеграл от иррациональной функции. Непосредственное интегрирование
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
|
Интегрирование биномиальных интегралов Так называемый биномиальный интеграл имеет следующий вид: . Такой интеграл берётся в трёх случаях. 1) Случай первый. Самый лёгкий. Если степень – целое число. Например: Представим интеграл в стандартном виде (это лучше делать на черновике): Мы видим, что степень – целая, а, значит, действительно имеет место первый случай. На самом деле биномиальный интеграл первого типа решается практически так же, как интегралы в примерах 5, 6, поэтому приводить почти такие же решения особого смысла нет – я просто покажу, какую замену здесь нужно провести. Смотрим на знаменатели дробей: 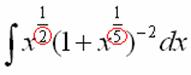 Записываем знаменатели: 2, 5. Находим наименьшее общее кратное этих чисел. Очевидно, это 10: оно делится и на 2 и на 5, кроме того – десятка самая маленькая в этом смысле. После замены все корни гарантировано пропадут. Повторюсь, примеров для первого случая не будет, так как они очень похожи на недавно разобранные интегралы. 2) Случай второй Если – целое число, то необходимо провести замену , где – знаменатель дроби . Спокойствие, только спокойствие, сейчас во всём разберемся. Пример 7 Найти неопределенный интеграл Представим интеграл в стандартном виде : Выписываем степени: , , Сразу проверяем, не относится ли наш интеграл к первому случаю? – целое? Нет. Проверяем второй случай: – целое, значит у нас второй случай Согласно правилу для второго случая, необходимо провести замену , где – знаменатель дроби . В рассматриваемом примере , и знаменатель этой дроби равен «двойке». Таким образом, чтобы гарантировано избавиться от корня, нужно провести замену . Оформляем решение: Проведем замену . После этой подстановки с корнем у нас будет всё гуд: Теперь нужно выяснить, во что превратится оставшаяся часть подынтегрального выражения Берем нашу замену и навешиваем дифференциалы на обе части: 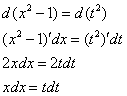 Но вот, незадача, у нас , а нам нужно выразить . Умножаем обе части на : Таким образом: . Уже лучше, но хотелось бы выразить только через , а в правой части – «икс» в квадрате внизу. Что делать? Вспоминаем нашу замену и выражаем из неё нужный нам . Окончательно: . Головоломно, но, увы, другие алгоритмы еще запутаннее. Собственно, всё готово, продолжаем решение: 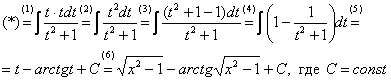 (1) Проводим подстановку согласно замене. (2) Записываем компактно числитель. (3) Раскладываем знаменатель в сумму. (4) Почленно делим числитель на знаменатель. (5) Интегрируем по таблице. (6) Проводим обратную замену: если , то Пример 8 Найти неопределенный интеграл Это пример для самостоятельного решения. Полное решение и ответ в конце урока. 3) Случай третий. Самый сложный Если – целое число, то необходимо провести замену , где – знаменатель дроби . Пример 9 Найти неопределенный интеграл Представим интеграл в стандартном виде : Выписываем степени и коэффициенты: , , , , 1) Не относится ли наш интеграл к первому случаю? – целое? Нет. 2) Проверяем второй случай: – целое? Нет. 3) – целое! Значит, у нас третий случай. Согласно правилу для третьего случая, необходимо провести замену , где – знаменатель дроби . В рассматриваемом примере , и знаменатель этой дроби равен опять же «двойке». Коэффициенты (будьте внимательны) , Таким образом, чтобы гарантировано избавиться от корня, нужно провести замену . Оформляем решение: Проведем замену: . Разбираемся с корнем. Это труднее, чем в предыдущих случаях. Сначала из нашей замены нужно выразить «икс квадрат»: Теперь подставляем под корень: 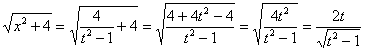 На втором этапе выясняем, во что превратится оставшаяся часть подынтегрального выражения . Берем нашу замену и навешиваем дифференциалы на обе части: 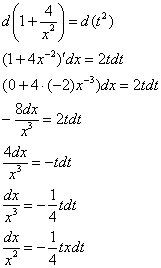 Опять проблема, в правой части у нас есть «икс», а нам нужно всё выразить через «тэ». Берем ранее найденное выражение и выражаем Окончательно: В итоге мы выразили через «тэ» и и , всё готово для продолжения решения:  (1) Проводим подстановку согласно замене. (2) Упрощаем выражение. (3) Меняем знак в знаменателе и выносим минус за пределы интеграла (можно было не делать, но так удобнее). (4) Проводим обратную замену. В третьем случае биномиального интеграла это тоже труднее. Если изначальная замена , то (5) Избавляемся от четырехэтажности в логарифме. Пример 10 Найти неопределенный интеграл Это пример для самостоятельного решения. Подсказка: здесь Полное решение и ответ только для выживших студентов. Что делать, если биномиальный интеграл не подходит ни под один из рассмотренных трех случаев? Это грустный четвертый случай. Такой интеграл является неберущимся. Почти всё рассмотрено. Есть другие разновидности интегралов с корнями, но они встречаются еще реже, чем биномиальные интегралы. Таким образом, материала данного урока вполне достаточно. Желаю успехов! Решения и ответы: Пример 2: Решение: Проведем замену: 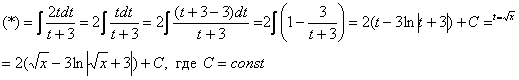 Пример 4: Решение: Проведем замену: . Навешиваем дифференциалы на обе части: Вот почему дифференциалы нужно именно НАВЕШИВАТЬ на обе части и добросовестно раскрывать эти дифференциалы. Немало чайников здесь формально напишет и допустит ошибку.  Пример 6: Решение: Замена:  Примечание: на самом деле данное решение не совсем рационально. Перед тем, как раскладывать числитель в сумму, лучше было поменять у знаменателя знак и сразу вынести минус за пределы интеграла: – в таком виде подбирать числитель значительно проще. Пример 8: Решение: , , , 1) – целое? Нет. 2) – целое, значит у нас второй случай. Замена: Если , то Окончательно: 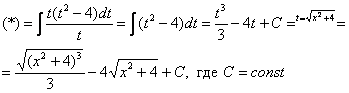 Пример 10: Решение: , , , , 1) – целое? Нет. 2) – целое? Нет. 3) – целое! Замена: , в данном случае: Разбираемся с корнем. Из : Тогда: 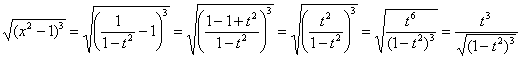 Оставшаяся часть подынтегрального выражения: 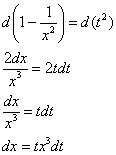 Чему равно ? Окончательно: 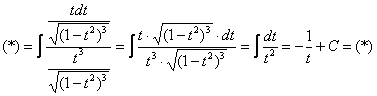 Обратная замена. Если , то 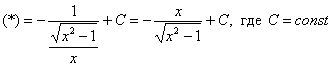 Метод разложение числителя Пример 1 Найти неопределенный интеграл. Выполнить проверку. На уроке Неопределенный интеграл. Примеры решений мы избавлялись от произведения функций в подынтегральном выражении, превращая её в сумму, удобную для интегрирования. Оказывается, что иногда в сумму (разность) можно превратить и дробь! Анализируя подынтегральную функцию, мы замечаем, что и в числителе и в знаменателе у нас находятся многочлены первой степени: и . Когда в числителе и знаменателе находятся многочлены одинаковой степени, то помогает следующий искусственный приём: в числителе мы должны самостоятельно организовать такое же выражение, что и в знаменателе: Рассуждение может быть следующим: «В числителе мне надо организовать , но если я прибавлю к «иксу» тройку, то, для того, чтобы выражение не изменилось – я обязан эту же тройку и вычесть». Теперь можно почленно разделить числитель на знаменатель: В результате мы добились, чего и хотели. Используем первые два правила интегрирования:  Готово. Проверку при желании выполните самостоятельно. Обратите внимание, что во втором интеграле – это «халявная» сложная функция, об особенностях ее интегрирования я рассказал на уроке Метод замены переменной в неопределенном интеграле. Кстати, рассмотренный интеграл можно решить и методом замены переменной, обозначая , но запись решения получится значительно длиннее Пример 2 Найти неопределенный интеграл. Выполнить проверку. Это пример для самостоятельного решения. Следует заметить, что здесь метод замены переменной уже не пройдёт. Внимание, важно! Примеры №№1,2 являются типовыми и встречаются часто. В том числе, подобные интегралы нередко возникают в ходе решения других интегралов, в частности, при интегрировании иррациональных функций (корней). Рассмотренный приём работает и в случае, если старшая степень числителя, больше старшей степени знаменателя. Пример 3 Найти неопределенный интеграл. Выполнить проверку. Начинаем подбирать числитель. Алгоритм подбора числителя примерно такой: 1) В числителе мне нужно организовать , но там . Что делать? Заключаю в скобки и умножаю на : . 2) Теперь пробую раскрыть эти скобки, что получится? . Хмм… уже лучше, но никакой двойки при изначально в числителе нет. Что делать? Нужно домножить на : 3) Снова раскрываю скобки: . А вот и первый успех! Нужный получился! Но проблема в том, что появилось лишнее слагаемое . Что делать? Чтобы выражение не изменилось, я обязан прибавить к своей конструкции это же : . Жить стало легче. А нельзя ли еще раз в числителе организовать ? 4) Можно. Пробуем: . Раскрываем скобки второго слагаемого: . Простите, но у меня вообще-то было на предыдущем шаге , а не . Что делать? Нужно домножить второе слагаемое на : 5) Снова для проверки раскрываю скобки во втором слагаемом: . Вот теперь нормально: получено из окончательной конструкции пункта 3! Но опять есть маленькое «но», появилось лишнее слагаемое , значит, я обязан прибавить к своему выражению : Если всё выполнено правильно, то при раскрытии всех скобок у нас должен получиться исходный числитель подынтегральной функции. Проверяем: Таким образом:  Готово. В последнем слагаемом я применил метод подведения функции под дифференциал. Если найти производную от ответа и привести выражение к общему знаменателю, то у нас получится в точности исходная подынтегральная функция . Рассмотренный метод разложения в сумму – есть ни что иное, как обратное действие к приведению выражения к общему знаменателю. Алгоритм подбора числителя в подобных примерах лучше выполнять на черновике. При некоторых навыках будет получаться и мысленно. Припоминаю рекордный случай, когда я выполнял подбор для 11-ой степени, и разложение числителя заняло почти две строчки Вёрда. Помимо алгоритма подбора можно использовать деление столбиком многочлена на многочлен, но, боюсь, объяснения займут еще больше места, поэтому как-нибудь в другой раз. Пример 4 Найти неопределенный интеграл. Выполнить проверку. Это пример для самостоятельного решения. Метод подведения под знак дифференциала для простейших дробей Переходим к рассмотрению следующего типа дробей. , , , (коэффициенты и не равны нулю). На самом деле пара случаев с арксинусом и арктангенсом уже проскальзывала на уроке Метод замены переменной в неопределенном интеграле. Решаются такие примеры способом подведения функции под знак дифференциала и дальнейшим интегрированием с помощью таблицы. Вот еще типовые примеры с длинным и высоким логарифмом: Пример 5 Пример 6 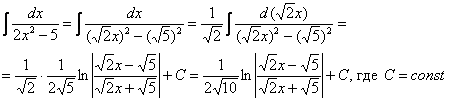 Тут целесообразно взять в руки таблицу интегралов и проследить, по каким формулам и как осуществляется превращение. Обратите внимание, как и зачем выделяются квадраты в данных примерах. В частности, в примере 6 сначала необходимо представить знаменатель в виде , потом подвести под знак дифференциала. А сделать это всё нужно для того, чтобы воспользоваться стандартной табличной формулой Да что смотреть, попробуйте самостоятельно решить примеры №№7,8, тем более, они достаточно короткие: Пример 7 Найти неопределенный интеграл: Пример 8 Найти неопределенный интеграл: Если Вам удастся выполнить еще и проверку данных примеров, то большой респект – Ваши навыки дифференцирования на высоте. Метод выделения полного квадрата Интегралы вида , (коэффициенты и не равны нулю) решаются методом выделения полного квадрата. На самом деле такие интегралы сводятся к одному из четырех табличных интегралов, которые мы только что рассмотрели. А достигается это с помощью знакомых формул сокращенного умножения: или Формулы применяются именно в таком направлении, то есть, идея метода состоит в том, чтобы в знаменателе искусственно организовать выражения либо , а затем преобразовать их соответственно в либо . Пример 9 Найти неопределенный интеграл Это простейший пример, в котором при слагаемом – единичный коэффициент (а не какое-нибудь число или минус). Смотрим на знаменатель, здесь всё дело явно сведется к случаю . Начинаем преобразование знаменателя: Очевидно, что нужно прибавлять 4. И, чтобы выражение не изменилось – эту же четверку и вычитать: Теперь можно применить формулу : После того, как преобразование закончено ВСЕГДА желательно выполнить обратный ход: , всё нормально, ошибок нет. Чистовое оформление рассматриваемого примера должно выглядеть примерно так: 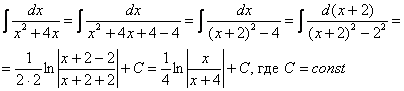 Готово. Подведением «халявной» сложной функции под знак дифференциала: , в принципе, можно было пренебречь Пример 10 Найти неопределенный интеграл: Это пример для самостоятельного решения, ответ в конце урока Пример 11 Найти неопределенный интеграл: Что делать, когда перед находится минус? В этом случае, нужно вынести минус за скобки и расположить слагаемые в нужном нам порядке: . Константу («двойку» в данном случае) не трогаем! Теперь в скобках прибавляем единичку. Анализируя выражение, приходим к выводу, что и за скобкой нужно единичку – прибавить: Тут получилась формула , применяем: |
