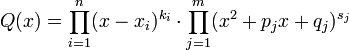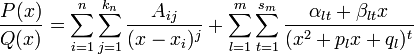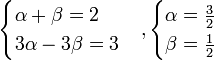интеграл от ирраци функции. Интеграл от иррациональной функции. Непосредственное интегрирование

• Название: Непосредственное интегрирование
• Анкор: интеграл от ирраци функции
• Дата: 16.01.2023
• Размер: 0.56 Mb.
• Имя файла: Интеграл от иррациональной функции.docx
• Тип: Документы; #889275
• страница: 1 из 5

Непосредственное интегрирование

Метод интегрирования, при котором интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием. См. Таблица интегралов.

[править] Подведение под знак дифференциала

Данный метод эквивалентен методу замены переменной (см. далее):

[править] Метод замены переменной (метод подстановки)

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.

Пусть требуется вычислить интеграл Сделаем подстановку где — функция, имеющая непрерывную производную.

Тогда и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:

[править] Интегрирование выражений вида

Если m нечётное, m > 0, то удобнее сделать подстановку sin x = t.

Если n нечётное, n > 0, то удобнее сделать подстановку cos x = t.

Если n и m чётные, то удобнее сделать подстановку tg x = t.

[править] Примеры

Вычислить:

Пусть тогда и

[править] Интегрирование по частям

Основная статья: Интегрирование по частям

Интегрирование по частям — применение следующей формулы для интегрирования:



В частности, с помощью n-кратного применения этой формулы находится интеграл



где P_{n + 1}(x) — многочлен (n + 1)-ой степени.

[править] Интегрирование рациональных дробей

Неопределенный интеграл от любой рациональной дроби на всяком промежутке, на котором знаменатель дроби не обращается в ноль, существует и выражается через элементарные функции, а именно он является алгебраической суммой суперпозиции рациональных дробей, арктангенсов и рациональных логарифмов.

Сам метод заключается в разложении рациональной дроби на сумму простейших дробей.

Всякую правильную рациональную дробь , знаменатель которой разложен на множители



можно представить (и притом единственным образом) в виде следующей суммы простейших дробей:



где A_ij,α_lt,β_lt — некоторые действительные коэффициенты, обычно вычисляемые с помощью метода неопределённых коэффициентов.

[править] Примеры

Вычислить:

Разложим подынтегральное выражение на простейшие дроби:



Сгруппируем слагаемые и приравняем коэффициенты при членах с одинаковыми степенями:

α(x + 3) + β(x − 3) = 2x + 3

(α + β)x + 3α − 3β = 2x + 3

Следовательно

Тогда

Теперь легко вычислить исходный интеграл

Интегрирование простейших рациональных дробей. Простейшие дроби, полученные при разложении произвольной правильной рациональной дроби, интегрируются с помощью следующих шести формул: У дробей с квадратичным знаменателем сначала необходимо выделить полный квадрат: 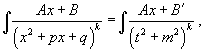где Затем при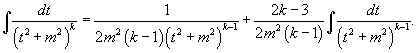меняются следующие формулы: Интеграл может быть вычислен за k шагов с помощью формулы редукции

Пример 1

Вычислить интеграл . Решение. Разложим подынтегральное выражение на простейшие дроби: Сгруппируем слагаемые и приравняем коэффициенты при членах с одинаковыми степенями: 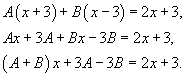Следовательно, 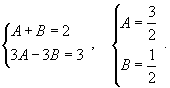Тогда 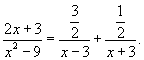Теперь легко вычислить исходный интеграл

Пример 2

Вычислить интеграл 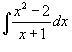. Решение. Сначала выделим правильную рациональную дробь, разделив числитель на знаменатель. Получаем

Пример 3

Вычислить интеграл . Решение.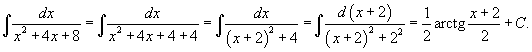

Пример 4

Вычислить интеграл . Решение. Разложим подынтегральное выражение на сумму простейших дробей, используя метод неопределенных коэффициентов: Определим ы: 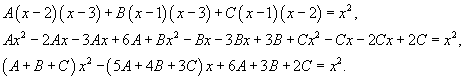Следовательно, 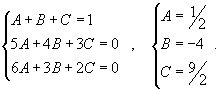Получаем 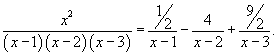Интеграл, соответственно, равен

Пример 5

Найти интеграл . Решение. Разложим подынтегральное выражение на сумму двух дробей. Найдем неизвестные коэффициенты. 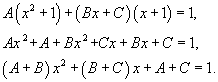Отсюда получаем 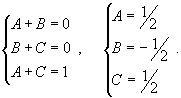Подынтегральное выражение представляется в виде 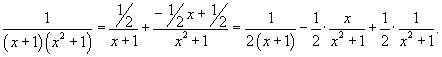Исходный интеграл равен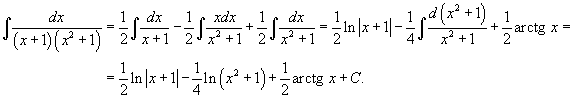

Пример 6

Найти интеграл . Решение. Разложим знаменатель в подынтегральном выражении на множители: Далее представим подынтегральное выражение в виде суммы простейших дробей Определим коэффициенты: 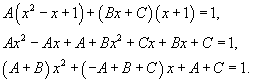Следовательно, 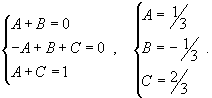Отсюда находим 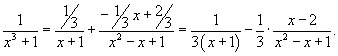Теперь вычислим исходный интеграл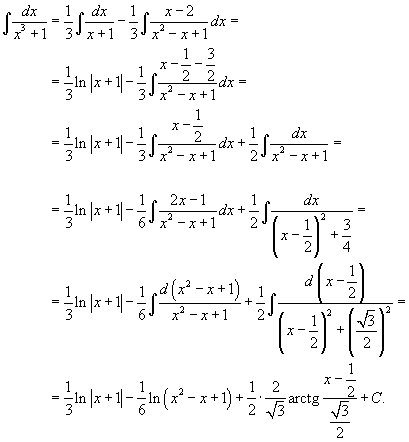

Пример 7

Вычислить интеграл . Решение. Перепишем знаменатель рациональной дроби в следующем виде: Поскольку полученные множители являются несократимыми квадратичными функциями, то подынтегральное выражение представляется в виде 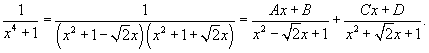Определим неизвестные коэффициенты. 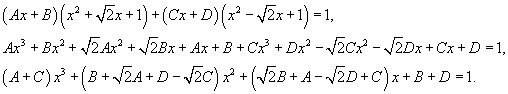Получаем 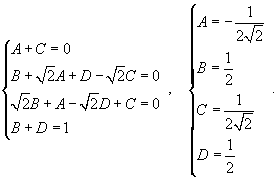Следовательно, 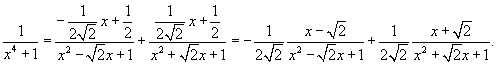Интегрируем каждое слагаемое и находим ответ.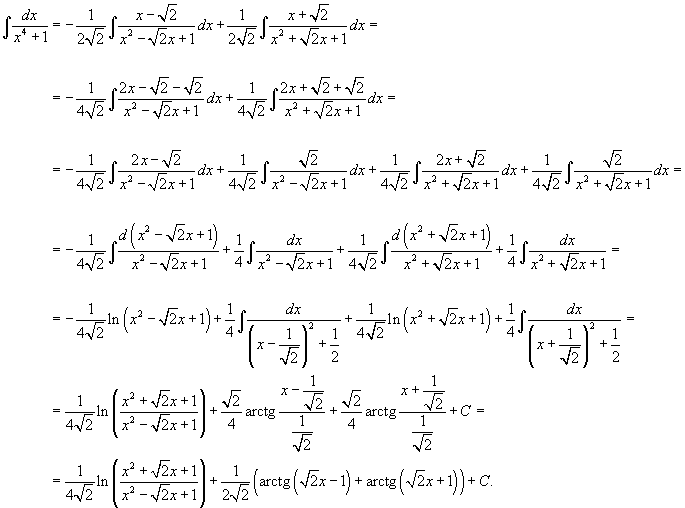

Пример 8

Вычислить интеграл . Решение. Разложим знаменатель на множители: Запишем подынтегральную дробь в виде суммы простейших дробей. Сгруппируем члены с одинаковыми степенями чтобы определить неизвестные коэффициенты из системы линейных уравнений. 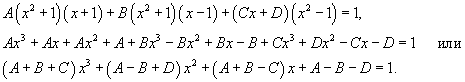Следовательно, 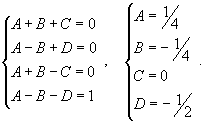Таким образом, подынтегральное выражение представляется в виде Окончательно находим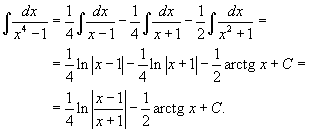

Пример 9

Вычислить интеграл . Решение. Разложим подынтегральное выражение на сумму простейших дробей, учитывая что знаменатель имеет кратный корень 3-го порядка: Определим неизвестные коэффициенты. 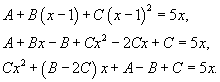Получаем систему уравнений 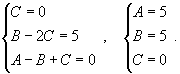Следовательно, Исходный интеграл равен

Пример 10

Вычислить интеграл 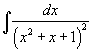. Решение. Поскольку 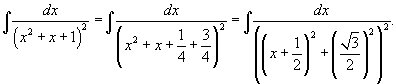- несократимый квадратный трехчлен, выделим в знаменателе полный квадрат: Найдем полученный интеграл с помощью формулы редукции 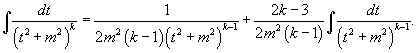Получаем ответ: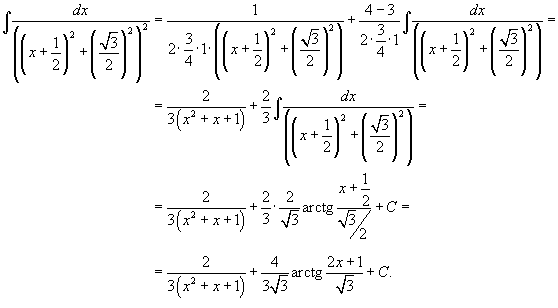