интеграл от ирраци функции. Интеграл от иррациональной функции. Непосредственное интегрирование
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
|
Строго следуйте алгоритму! Если Вы разобрались, по каким принципам нужно раскладывать дробно-рациональную функцию в сумму, то сможете разгрызть практически любой интеграл рассматриваемого типа. Пример 5 Найти неопределенный интеграл. Шаг 1. Очевидно, что дробь является правильной: Шаг 2. Можно ли что-нибудь разложить в знаменателе на множители? Можно. Здесь сумма кубов . Раскладываем знаменатель на множители, используя формулу сокращенного умножения Шаг 3. Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей: Обратите внимание, что многочлен неразложим на множители (проверьте, что дискриминант отрицательный), поэтому вверху мы ставим линейную функцию с неизвестными коэффициентами, а не просто одну буковку. Приводим дробь к общему знаменателю: Составим и решим систему: 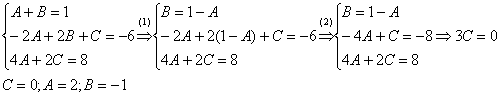 (1) Из первого уравнения выражаем и подставляем во второе уравнение системы (это наиболее рациональный способ). (2) Приводим подобные слагаемые во втором уравнении. (3) Почленно складываем второе и третье уравнения системы. Все дальнейшие расчеты, в принципе, устные, так как система несложная. 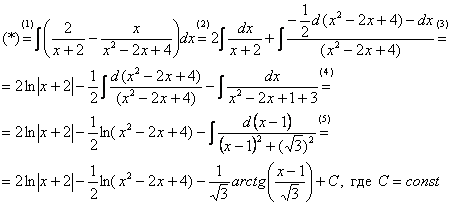 (1) Записываем сумму дробей в соответствии с найденными коэффициентами . (2) Используем свойства линейности неопределенного интеграла. Что произошло во втором интеграле? С этим методом Вы можете ознакомиться в последнем параграфе урока Интегрирование некоторых дробей. (3) Еще раз используем свойства линейности. В третьем интеграле начинаем выделять полный квадрат (предпоследний параграф урока Интегрирование некоторых дробей). (4) Берём второй интеграл, в третьем – выделяем полный квадрат. (5) Берём третий интеграл. Готово. А вот вам еще пара примеров для самостоятельного решения, один похожий, другой – труднее. Пример 6 Найти неопределенный интеграл. Пример 7 Найти неопределенный интеграл. Интегрирование неправильной дробно-рациональной функции Перейдем к рассмотрению случая, когда старшая степень числителя больше либо равна старшей степени знаменателя. Пример 8 Найти неопределенный интеграл. Совершенно очевидно, что данная дробь является неправильной: Основной метод решения интеграла с неправильной дробно-рациональной функций – это деление числителя на знаменатель. Да-да, делить будем столбиком, как самые обычные числа в школе. Напоминаю алгоритм. Сначала рисуем «заготовку» для деления: 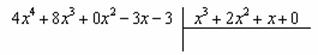 ВСЕ недостающие степени (и (или) свободные члены) без пропусков записываем в ОБОИХ многочленах с нулевыми коэффициентами. Теперь маленькая задачка, на какой множитель нужно умножить , чтобы получить ? Очевидно, что на : 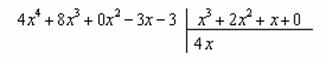 Далее умножаем сначала на , потом – на , потом – на , потом – на 0 и записываем результаты слева: 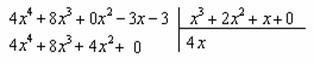 Проводим черточку и производим вычитание (из верха вычитаем низ): 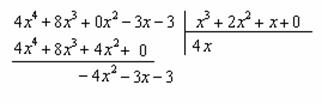 Старшая степень остатка равна двум, старшая степень делителя – больше, она равна трём, значит, больше разделить не удастся. Если бы изначально у нас был в числителе многочлен пятой степени, то то алгоритм деления увеличился бы на один шаг. Итак, наше решение принимает следующий вид: Делим числитель на знаменатель: 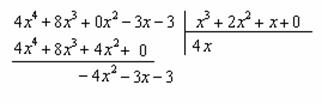 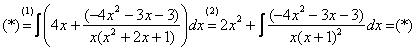 (1) Что дало деление? Много хорошего: теперь у нас два слагаемых, первое – интегрируется совсем просто, а второе – правильная дробь, которую мы решать уже умеем. После деления всегда желательно выполнять проверку. В рассматриваемом примере можно привести к общему знаменателю , и в результате получится в точности исходная неправильная дробь (2) От первого слагаемого сразу берем интеграл. Знаменатель дроби раскладываем на множители Дальше всё идет по накатанной схеме: Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей: 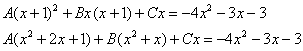 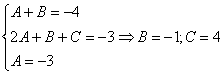 Готово. И, наконец, заключительный пример для самостоятельного решения. Он очень интересен, рекомендую всем! Пример 9 Найти неопределенный интеграл. Только что обратил внимание, что во всех примерах урока в ходе решения систем у нас получались «хорошие» целые коэффициенты . По той причине, что почти все интегралы я взял из сборника Рябушко. На практике же Таким образом, если в ходе решения интеграла от дробно-рациональной функции у Вас получаются дробные значения коэффициентов , то в этом нет ничего страшного, ситуация даже обыденна. Желаю успехов! Решения и ответы: Пример 2: Решение: Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей: 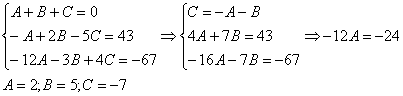 Комментарий: в правой части у нас нет слагаемого с , поэтому в первом уравнении системы ставим справа ноль. Пример 4: Решение: Шаг 1. Проверяем, правильная ли у нас дробь Старшая степень числителя: 6 Старшая степень знаменателя: 8 , значит, дробь является правильной. Шаг 2. Можно ли что-нибудь разложить в знаменателе на множители. Множитель разложить нельзя, а вот – можно: 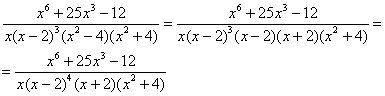 Шаг 3. Представим дробно-рациональную функцию в виде суммы элементарных дробей. В данном случае, разложение имеет следующий вид: Пример 6: Решение: Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей: 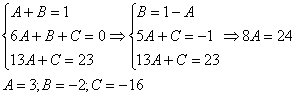  Пример 7: Решение: Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей: 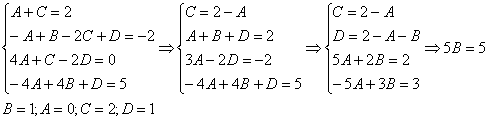 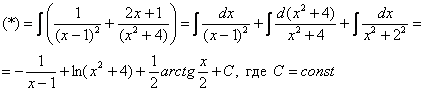 Пример 9: Решение: 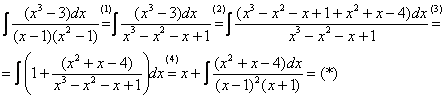 (1) Здесь неправильная дробь, поскольку старшие степени числителя и знаменателя равны: 3 = 3. Для того чтобы разделить числитель на знаменатель придётся временно раскрыть скобки в знаменателе. (2)-(3) Теперь можно разделить на знаменатель , но делать этого… я не буду. Можно поступить хитрее. Используем прием, который рассмотрен в первом параграфе урока Интегрирование некоторых дробей. (4) От первого слагаемого сразу берем интеграл. Знаменатель оставшейся, уже правильной, дроби снова записываем в виде произведения множителей. Тут я немного подсократил разложение, надеюсь, всем понятно, что Далее накатанная колея… Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей: 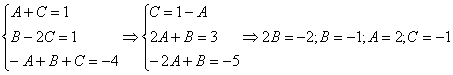 Иррациональные функции Пример 1 Найти неопределенный интеграл Анализируя подынтегральную функцию, приходишь к печальному выводу, что она совсем не напоминает табличные интегралы. Вот если бы всё это добро находилось в числителе – было бы просто. Или бы корня внизу не было. Или многочлена. Никакие методы интегрирования дробей тоже не помогают. Что делать? Основной приём решения иррациональных интегралов – это замена переменной, которая избавит нас от ВСЕХ корней в подынтегральной функции. Отмечу, что эта замена немного своеобразная, ее техническая реализация отличается от «классического» способа замены, который рассмотрен на уроке Метод замены в неопределенном интеграле. В данном примере нужно провести замену , то есть, вместо «икса» под корнем у нас окажется . Почему замена именно такая? Потому-что , и в результате замены корень пропадёт. Если бы в подынтегральной функции вместо квадратного корня у нас находился , то мы бы провели замену . Если бы там был – то и так далее. Хорошо, у нас превратится в . Что произойдет с многочленом ? Сложностей нет: если , то . Осталось выяснить, во что превратится дифференциал . Делается это так: Берем нашу замену и навешиваем дифференциалы на обе части: (я распишу максимально подробно) Оформление решения должно выглядеть примерно так: Проведем замену:  (1) Проводим подстановку после замены (как, что и куда, уже рассмотрено). (2) Выносим константу за пределы интеграла. Числитель и знаменатель сокращаем на . (3) Получившийся интеграл является табличным, готовим его для интегрирования, выделяя квадрат (4) Интегрируем по таблице, используя формулу . (5) Проводим обратную замену. Как это делается? Вспоминаем, от чего плясали: если , то . Внимание! Для изучения дальнейших примеров необходимо хорошо проработать первый параграф урока Интегрирование некоторых дробей. Пример 2 Найти неопределенный интеграл Это пример для самостоятельного решения. Полное решение и ответ в конце урока. Как-то так получилось, что в примерах 1, 2 «голый» числитель с одиноким дифференциалом . Что же. Исправим ситуацию. Пример 3 Найти неопределенный интеграл Предварительный анализ подынтегральной функции опять показывает, что лёгкого пути нет. А поэтому нужно избавляться от корня. Проведем замену: За обозначаем ВСЁ выражение под корнем. Замена из предыдущих примеров здесь не годится (точнее, сделать-то её можно, но это не избавит нас от корня). Навешиваем дифференциалы на обе части: С числителем разобрались. Что делать с в знаменателе? Берем нашу замену и выражаем из неё: Если , то 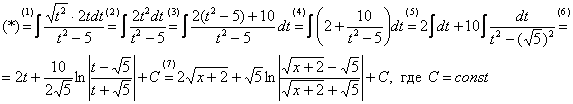 (1) Проводим подстановку в соответствии с выполненной заменой. (2) Причесываем числитель. Константу здесь я предпочел не выносить за знак интеграла (можно делать и так, ошибкой не будет) (3) Раскладываем числитель в сумму. Еще раз настоятельно рекомендую ознакомиться с первым параграфом урока Интегрирование некоторых дробей. Канители с разложением числителя в сумму в иррациональных интегралах будет предостаточно, очень важно отработать это прием. (4) Почленно делим числитель на знаменатель. (5) Используем свойства линейности неопределенного интеграла. Во втором интеграле выделяем квадрат для последующего интегрирования по таблице. (6) Интегрируем по таблице. Первый интеграл совсем простой, во втором используем табличную формулу высокого логарифма (7) Проводим обратную замену. Если мы проводили замену , то, обратно: Пример 4 Найти неопределенный интеграл Это пример для самостоятельного решения, если вы невнимательно проработали предыдущие примеры, то допустите ошибку! Полное решение и ответ в конце урока. Принципиально так же решаются интегралы с несколькими одинаковыми корнями, например , и т.д. А что делать, если в подынтегральной функции корни разные? Пример 5 Найти неопределенный интеграл 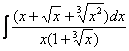 Вот и пришла расплата за голые числители. Когда встречается такой интеграл, обычно становится страшно. Но страхи напрасны, после проведения подходящей замены подынтегральная функция упрощается. Задача состоит в следующем: провести удачную замену, чтобы сразу избавиться от ВСЕХ корней. Когда даны разные корни удобно придерживаться следующей схемы решения. Сначала выписываем на черновике подынтегральную функцию, при этом все корни представляем в виде : . Нас будут интересовать знаменатели степеней: 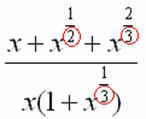 Записываем эти знаменатели: 2, 3, 3. Теперь нужно найти наименьшее общее кратное чисел 2, 3, 3 – такое число, чтобы оно делилось и на 2 и на 3 (в данном случае), кроме того, это число должно быть как можно меньше. Очевидно, что наименьшим общим кратным является число 6. Оно делится и на 2 и на 3, кроме того, меньше шестерки ничего не придумать. Как многие уже догадались, замена в рассматриваемом интеграле будет следующей: Оформляем решение: 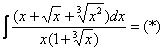 Проведем замену: 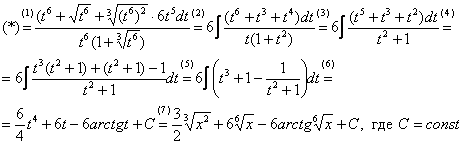 (1) Производим подстановку. (2) Избавляемся от корней. Выносим константу за знак интеграла. Сокращаем числитель и знаменатель на . (3) Сокращаем числитель и знаменатель еще на . (4) Раскладываем числитель в сумму (как это сделать, уже неоднократно упоминалось). (5) Почленно делим числитель на знаменатель. (6) Интегрируем по таблице. При этом константу я снова «прилепил» к каждому из трех слагаемых (можно этого и не делать, момент несущественный). (7) Проводим обратную замену. Если , то, обратно: . В ходе обратной замены некоторые корни лучше сразу сократить (обычно это делается устно). В рассмотренном примере сокращение корней встретилось в первом слагаемом: Как видите, особых сложностей нет, несмотря на то, что сначала интеграл показался трудным и страшным. Пример 6 Найти неопределенный интеграл Это пример для самостоятельного решения. |
