5 класс. 5 класс -Задания повышенного уровня сложности по математике. Обозначение натуральных чисел
 Скачать 410 Kb. Скачать 410 Kb.
|
|
Шкалы и координаты. Меньше или больше. а) На координатном луче отмечены точки А(а), В( а+3), С(а-4), М( а+1). Единичный отрезок равен 4см. Чему равны длины отрезков АМ и ВС? Каковы координаты точек, удаленных от точки М на 12см? б) На координатном луче отмечены точки А(с), В( с+3), С(с-2), М( с+4). Единичный отрезок равен 5см. Чему равны длины отрезков АВ и СМ? Каковы координаты точек, удаленных от точки В на 20см? Расположите числа, в которых некоторые разряды заменены звездочками, в порядке а) убывания: ***4**5*, ***5*4*, ***5**4*, ***4*5*. б) возрастания : 8*8*88**, *8*8*8*, 9***999*, 99****9. 3. Запишите в виде двойного неравенства зависимость между тремя величинами: а) 6т 24кг, 6240кг и 62ц4кг б) 53ц 2кг, 5320кг и 5т 32кг 4. а) Запишите наибольшее и наименьшее натуральные числа, содержащие цифру 9 в разряде десятков, если эти числа больше 50099 и меньше 5000090. б) Запишите наибольшее и наименьшее натуральные числа, содержащие цифру 9 в разряде сотен, если эти числа больше 900999 и меньше 8000900. а) К какому трехзначному числу надо прибавить наибольшее двузначное число, чтобы получилось наибольшее трехзначное число? б) К какому трехзначному числу надо прибавить наименьшее трехзначное число, чтобы получилось наименьшее четырехзначное число? равны суммы 1 + 3 + 5 + 7 + 9 + 11 1 + 3 + 5 + 7 + 9 + 11 + 13 Сколько слагаемых надо взять, чтобы сумма была равна 100? Вычитание натуральных чисел. Выполните вычитание: а) 509 307 406 101 – 99 878 786 597 г) 780 730 560 100 – 87 948 975 672 б) 1 000 001 010 – 999 888 777 д) 1 500 000 003 – 999 666 888 в) 63ч 16мин – 48ч 37мин е) 72ч 23мин – 34ч 49мин Найдите разность а) наибольшего и наименьшего из чисел, составленных из цифр числа 6 800 351 б) наибольшего и наименьшего из чисел, составленных из цифр числа 4 760 002. Найдите значение выражения наиболее удобным способом: а) 739 102 – ( 39102 – 20 989 ) б) 831 762 – ( 31 762 – 15 999 ) а) В книге 234 страницы. Вася в понедельник прочитал 48 страниц, а за каждый из двух последующих дней он читал на 10 страниц меньше, чем в предыдущий. Сколько всего дней потратил Вася на чтение книги, если с четверга он читал по 30 страниц? б) Туристы наметили проплыть на байдарках 174 км. В первый день они проплыли 42км, а за каждый из двух последующих дней они проплывали на 8 км меньше, чем в предыдущий. В остальные дни они плыли по 24км в день. Сколько всего дней туристы были в пути? Как изменится разность двух чисел, если а) уменьшаемое уменьшить на 24, а вычитаемое уменьшить на 32? б) уменьшаемое увеличить на 26, а вычитаемое увеличить на 18? Восстановите размазанные цифры и впишите их в рамочки а) -7 5 8 б) - 3 2 в) - 1 2 0 0 г)- 0 0 0 0 0 2 8 1 2 9 2 9 3 2 --------------- ------------- ---------------- ---------------- 4 5 4 5 7 5 7 9 7 1 2 8 6 2 8 Продолжи каждый из рядов: а) 1, 0 , 1 , 0, 0, 1, 0, 0, 0,… в) 1, 9 , 3 , 11 , 5 , 13 ,… б) 2, 1, 4 ,3, 6 , 5, 8 , 7, … г) 5 , 6, 15, 12, 25, 18,… (*)Некто имеет 12 пинт меда и хочет отлить из этого количества половину, но у него нет сосуда вместимостью в 6 пинт. У него два сосуда : один вместимостью в 8 пинт, а другой вместимостью в 5пинт. Каким образом налить 6пинт меда в сосуд на 8пинт? Какое наименьшее число переливаний необходимо сделать при этом? (*) Рассудительная Оля записала некоторое трехзначное число, затем нашла сумму его цифр и записала результат, дальше нашла сумму цифр последнего числа и записала результат. Все эти три числа можно записать так: ( одинаковые фигуры соответствуют одинаковым цифрам) Восстановите запись чисел, которую выполнила Оля. Составьте буквенное выражение для решения задачи и упростите его: а) В питомнике вырастили а саженцев декоративных кустарников: поровну саженцев самшита и облепихи и поровну саженцев барбариса и вереска, а остальные саженцы – лещина. Вереска вырастили на 80 кустов больше, чем облепихи, а барбариса – 140 кустов. Сколько кустов лещины вырастили в питомнике? Вычислить при а =600. б) В парке растет у хвойных деревьев: сосен = 65 деревьев, и это на 14 больше, чем елей, кипарисов – на 12 больше, чем лиственниц, а лиственниц и елей поровну. Остальные деревья – кедры. Сколько кедров растет в парке? Вычислить при у=420. Решение уравнений. Решите уравнения: а) а – 6781 = 6781 е) х – 8900 = 8900 б) 67459 – с = 9999 ж) 98427 – у = 8888 в) ( 524 – х ) – 133 = 207 з) 945 – ( 697 – к ) = 349 г) 67 – ( 34 + у) + 56 = 73 и) 78 + ( 84 – х) -13 = 92 д) 98 – (( 45 + р) – 38 ) = 42 к) 69 – ( 97 – ( 28 + к)) = 45 а) Учитель задумал число. После этого он составил разность 52 и суммы задуманного числа и 15. Полученный результат он вычел из 43 и получил 17. Какое число задумал учитель? б) Учитель задумал число. После этого он составил сумму 67 и разности 36 и задуманного числа. Полученный результат он вычел из 88 и получил 12. Какое число задумал учитель? Решите задачу с помощью уравнения: а) Из бочки взяли 25л воды и дважды по 18л, а затем долили 30л, после чего в бочке стало 143л воды. Сколько литров воды было в бочке первоначально? б) В цистерну залили 12т нефти, а потом дважды по 14т. После того, как из цистерны забрали 22т, в ней осталось 128т нефти. Сколько тонн нефти было в цистерне первоначально? Какие из чисел 1, 2 , 4, 8 являются корнями уравнения а) х ∙ х + 14 = 7 ∙ х + 8 : х б) х + 56 : х = 14 + 64 : х : х Каким числом необходимо заменить а , чтобы корнем уравнения а) х + 6 =а было число 12? б) 35 – ( а + 12) = х + 12? Какими натуральными числами необходимо заменить а и с , чтобы корнем уравнения а) (11 – а) + ( х – с) = 16 было число 7? б) ( х – а) + ( 12 – с ) = 18 было число 8? Вместо квадратиков запишите такие числа, чтобы все уравнения имели один и тот же корень 2: а) 3х + 5 = б) 7х – 4 = в) - 11х = 12 Вставить в пустые клетки знаки действий и получите уравнения, решите их: а) 6 х = 3 2, х =…. г) 6 х = 3 2, х =…. ж) 6 х = 3 2, х =…. б) 6 х = 3 2, х =…. д) 6 х = 3 2, х =…. в) 6 х = 3 2, х =…. е) 6 х = 3 2, х =…. Деление натуральных чисел. Выполните деление: а) 98044 : 386 д) 123211 : 487 б) 56114054 : 7009 е) 56095036 : 8009 в) 1234566000 : 900 ж) 1097392000 : 800 г) 46493184 : 512 з) 49676898 : 614 Решите уравнения: а) а : 67 = 670 г) с : 56 = 560 б) 3220 : к = 35 д) 3735 : у = 45 в) ( 214 – 7с) ∙ 42 = 5460 е) 25 ∙ ( 328 – 8к ) = 5400 Найдите наименьшее число, которое а) при делении на 3, на 5 и на 13 дает в остатке 1. б) при делении на 7, на 5 и на 11 дает в остатке 2. а) Таня и Витя одновременно начали читать одинаковые книги , причем Витя читает в 4 раза медленнее Тани. Через три дня выяснилось, что Таня прочитала 144 страницы, а Вите осталось прочитать 396 страниц. Через сколько дней дочитает книгу Таня? б) Даша и Миша начали одновременно переплывать реку. Миша плывет в 3 раза быстрее Даши. Через 4 минуты выяснилось, что Даша проплыла 24м, а Мише осталось проплыть 36м. Через сколько минут переплывет реку Даша? а) Известно, что А меньше В в 6 раз, а В больше С в 2 раза. Какое из двух чисел больше – А или С? Во сколько раз? б) Известно, что А больше В в 12 раз, а В меньше С в 4 раза. Какое из двух чисел больше – А или С? Во сколько раз? Восстановите размазанные цифры и впишите их в окошки. _ 1 4 │ 7 5 │ _ 1 0 Делитель увеличили в 6 раз. Как надо изменить делимое, чтобы а) частное увеличилось в 2 раза? б) частное уменьшилось в 3 раза? Таня получила остаток 10 при делении 153 на некоторое число. На какое число делила Таня? Сколько решений имеет задача? Подставьте вместо звездочек такие знаки действий, чтобы равенства были верными: а) 4 * 4 * 13 = 13 б) 21 * 8 * 8 = 21 Подставьте вместо звездочек такие знаки действий, чтобы выполнялся порядок действий, указанный римскими цифрами. Можно пользоваться скобками. I II II I I II III а) 15 * 3 * 2 б) 48 * 9 * 3 в) 64 * 8 * 4 * 2 II I I III II г) 49 * 7 = 7 д) 39 * 7 * 6 = 3 е) 29 * 11 * 17 * 7 = 4 Задумай число. Умножь его на 5. Полученное произведение умножь на 2. Результат раздели на 10. В результате получилось задуманное число? Почему ? Формулы. Найдите по формуле пути: а) путь, если v =12км/ч, t = 30мин б) скорость, если S = 60м, t = 120 мин в) время, если S = 6км, v = 300 м/мин а) Периметр пятиугольника равен Р см. Первая сторона равна а см, а каждая следующая на 2см больше предыдущей стороны. Запишите формулу для нахождения четвертой стороны пятиугольника. б) Периметр пятиугольника равен Р см. Первая сторона равна а см, а каждая следующая в 2раза больше предыдущей стороны. Запишите формулу для нахождения пятой стороны пятиугольника. Из города выехал автомобиль со скоростью 74 км/ч. Через 1ч в противоположном направлении выехал мотоциклист со скоростью 36 км/ч. Чему равно расстояние S между ними через t часов после выезда мотоциклиста? Запишите ответ в виде формулы и упростите ее. Через сколько часов расстояние между ними будет равно 404км ? а) Известно, что у = ( 2х – а ) : с. Выразите переменные а, с, х из этой формулы б) Известно, что у = с : ( а – 3х). Выразите переменные а, с, х из этой формулы в) Из формулы у = ( 2а – 3с) : 40 выразите а, с. Площади. а) Периметры квадрата и прямоугольника равны. Площадь квадрата равна 36а. Длина прямоугольника в 4 раза меньше ширины. Найти площадь прямоугольника и выразите ее в арах. б) Площадь квадрата равна 25а, а его периметр в 2 раза меньше периметра прямоугольника. Длина прямоугольника на 40м больше ширины. Найти площадь прямоугольника и выразите ее в арах. От прямоугольного участка земли площадью 1га и шириной 40м отделили участок площадью 28 соток. Каков периметр оставшейся части?  6мммммм 6м  6м 8м 3м  От прямоугольного листа отрезали 2 прямо- От прямоугольного листа отрезали 2 прямо-угольника. Найдите периметр полученной фигуры. Найдите площадь полученной фигуры. Сколько краски потребуется для окрашивания фигуры с двух сторон, если на 1м а) Как изменится площадь прямоугольника , если длину увеличить в 12 раз, а ширину уменьшить в 3 раза? б) Как изменится площадь прямоугольника , если длину уменьшить в 24 раза, а ширину увеличить в 8 раз? Окружность и круг. Доли. Обыкновенные дроби. Начертите две окружности с центром в точке О и радиусами 2см 3мм и 3см 2мм. Через точку О проведите горизонтальную прямую, пересекающую обе окружности. Обозначьте четыре точки ее пересечения с окружностями слева направо А, М, Н,В. Как называются отрезки ОА и МН и какова их длина? Вычислите АМ и МВ. а) Бабушка испекла 48 пирогов. За завтраком съели 5 пирогов, а за обедом – в 3 раза больше. Какая часть всех пирогов осталась на ужин? Б) В классе 34 ученика. После уроков 14 человек пошли играть в баскетбол, в 2 раза меньше – в волейбол, а остальные – в футбол. Какая часть класса пошла играть в футбол? а) на приготовление обеда ушло 4кг овощей. Из них 7/20 ушло на борщ, 5/13 остатка – на салат, а остальные – на рагу. Сколько граммов овощей ушло на каждое блюдо? Б) Пятачок и Вини-Пух принесли кролику трехкилограммовый торт. Вини-Пух съел 13/15 торта, Кролик – ¾ остатка, а остальное – Пятачок. Сколько граммов торта съел каждый? а) На выполнение домашнего задания по математике Митя затратил ¾ часа, что составило 5/9 времени, затраченного на выполнение всех домашних заданий. Сколько времени Митя делал все домашние задания? б) Папа ехал троллейбусом 7/12 часа, что составляет 5/7 времени, затраченного на путь до работы. Сколько времени папа добирался до работы? Найдите полторы трети от 100; от 200. Два десятилитровых ведра полностью наполнены водой. Из первого сначала выливают ½ ведра воды, потом выливают 1/5 оставшегося количества воды. Из второго, наоборот, сначала выливают 1/5 ведра воды, а потом ½ оставшегося количества воды. В каком ведре останется воды больше? Витя Верхоглядкин – отличный хоккеист. Недавно он принял участие в матче за честь школы. Игра продолжалась два периода по 30 минут. Третью часть матча Витя подбирал себе коньки, клюшку и одевался в хоккейную форму, 2/3 матча он сидел на скамейке запасных. Остальное время Витя играл. Сколько шайб он забросил? Школьники сдали в аптеку 12 кг сушеной малины и 10 кг сушеной черники. Сколько свежих ягод они собрали, если малина при сушке теряет ¾ своего веса, а черника – 4/5 своего веса ? Одна сторона треугольника равна с см, вторая составляет 2/5 длины первой стороны, а третья – 15/100 длины первой стороны. Каков периметр треугольника? Ткань во время стирки садится на 1/16 часть по длине и на 1/15 часть по ширине. Какой длины надо взять кусок ткани, чтобы после стирки иметь 378м Ширина прямоугольного параллелепипеда равна 20см, что составляет 4/5 его длины. Высота параллелепипеда составляет 2/9 суммы его длины и ширины. Чему равен объем параллелепипеда? Установи закономерности и запиши еще по 2 числа в каждом ряду: а) 9 15, 27, 45, 69, … в) 4, 8, 8, 11, 16, 14, 32, 17, … б) 342, 313, 284, 255, … г) 3, 7, 16, 35, 74, 153, … в) 2. Решите уравнения: а) в) 3. а) За 2 часа водой заполняется 5/17 бассейна , а выливается 3/17 бассейна. На какую часть изменится уровень воды в бассейне через 6 часов? б) На бензозаправочной станции за 3 суток заполняется бензином 17/20 цистерны, а 15/20 цистерны расходуется. На какую часть изменится уровень бензина в цистерне через 9 суток? а) Саша расчистил от снега 6/11 двора, а затем еще 8м расчистить 3/11 двора. Какова площадь двора? б) Валя прочитала 5/12 журнала и еще 6 страниц, после чего Вале осталось прочитать 4/12 журнала. Сколько страниц в журнале? Вместо квадратиков запишите такие равные дроби, чтобы равенства были верными: + = 1 + + = 1 + + + = 1 Деление и дроби. Смешанные числа. Дедушка разлил 11кг меда в 6 больших банок и 5кг меда в 6 маленьких банок. На сколько килограммов меда больше в большой банке, чем в маленькой. Решите уравнения: а) в) 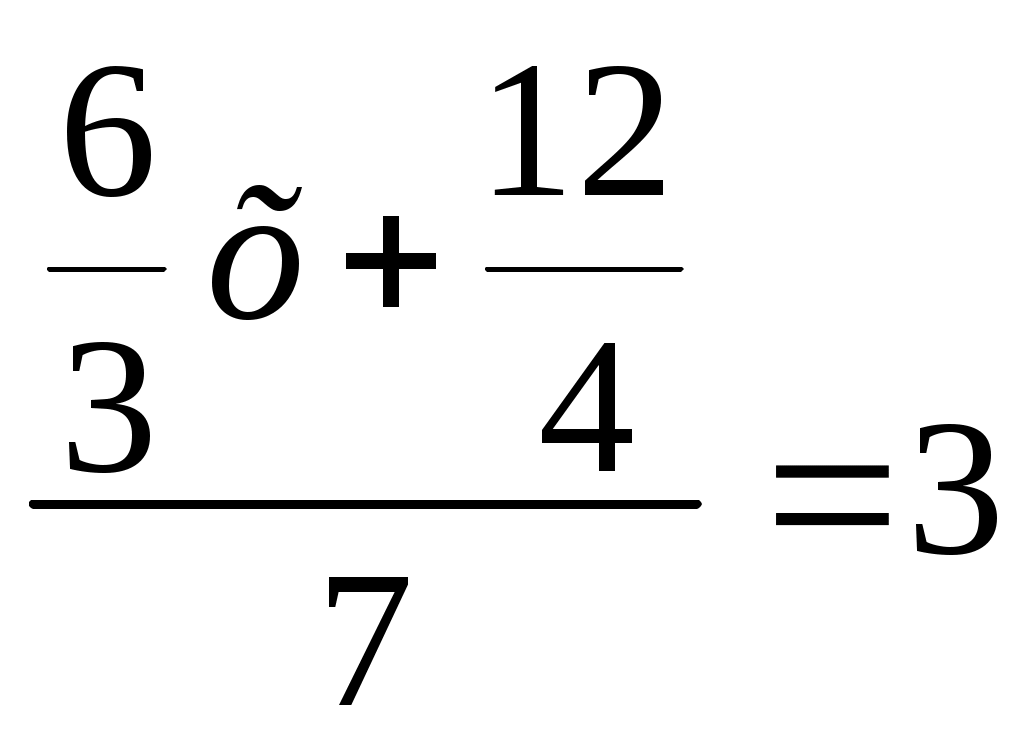 г) г) 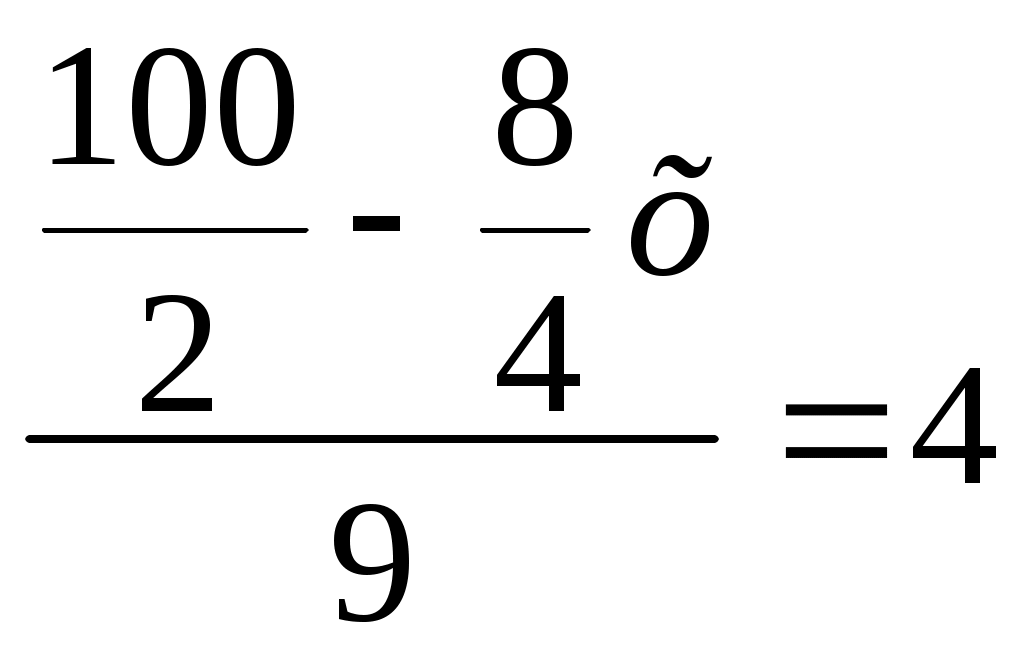 Выделите целую часть из дробей: Запишите в виде неправильной дроби Выразите: а) в метрах: 6см 8мм; 3дм 6см б) в часах: 3ч 48мин; 5мин 10с Вместо треугольников запишите такие числа, чтобы равенства были верными: |
