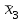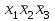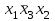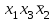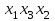Образовательная программа среднего профессионального образования Комплект контрольнооценочных средств по учебным
 Скачать 0.96 Mb. Скачать 0.96 Mb.
|
Законы логики (свойства логических операций)Следующие формулы являются законами логики. 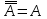 - закон двойного отрицания. - закон двойного отрицания.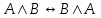 - закон коммутативности конъюнкции. - закон коммутативности конъюнкции.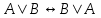 - закон коммутативности дизъюнкции. - закон коммутативности дизъюнкции. - закон ассоциативности конъюнкции. - закон ассоциативности конъюнкции.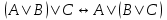 - закон ассоциативности дизъюнкции. - закон ассоциативности дизъюнкции.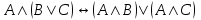 - закон дистрибутивности конъюнкции относительно дизъюнкции. - закон дистрибутивности конъюнкции относительно дизъюнкции.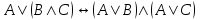 - закон дистрибутивности дизъюнкции относительно конъюнкции. - закон дистрибутивности дизъюнкции относительно конъюнкции.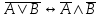 - закон отрицания дизъюнкции. - закон отрицания дизъюнкции.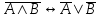 - закон отрицания конъюнкции. - закон отрицания конъюнкции.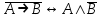 - закон отрицания импликации. - закон отрицания импликации.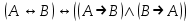 - закон выражения эквивалентности через конъюнкцию и импликацию. - закон выражения эквивалентности через конъюнкцию и импликацию. - закон контрапозиции. - закон контрапозиции.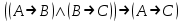 - закон силлогизма. - закон силлогизма. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Упрощение формул логики с помощью равносильных преобразований. Определение. Формула B есть логическое следствие формул A1, A2, .., An, если формула B принимает истинное значение при тех же значениях, при которых истинна каждая из формул A1, A2, .., An. Запись (A1, A2, .., An)B означает, что B – логическое следствие формул A1, A2, .., An. Пример. (AB, A 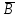 ) )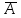 . .Докажем данное следствие.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Булевы функции. Переменная х, принимающая значения 0 или 1, называется булевой (или логической, двоичной). Функция F, зависящая от булевых переменных  и принимающая также значения 0 или 1, называется булевой (или логической, двоичной) и обозначается и принимающая также значения 0 или 1, называется булевой (или логической, двоичной) и обозначается 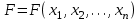 . .Булевы функции F от n переменных  могут быть заданы посредством таблицы истинности, содержащей могут быть заданы посредством таблицы истинности, содержащей 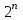 строк и строк и 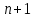 столбцов. В левой части таблицы содержатся наборы значений n переменных, расположенные в порядке возрастания их десятичного эквивалента, а в правой ее части значения функции F на соответствующих наборах значений переменных. столбцов. В левой части таблицы содержатся наборы значений n переменных, расположенные в порядке возрастания их десятичного эквивалента, а в правой ее части значения функции F на соответствующих наборах значений переменных.В качестве примера рассмотрим таблицу истинности некоторой булевой функции F, зависящей от переменных 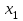 , ,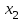 и и 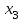 . .
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Совершенная дизъюнктивная и конъюнктивная нормальные формы (СДНФ и СКНФ) Определение. Элементарной конъюнкцией называется конъюнкция литералов (переменных или их отрицаний), взятых не более чем по одному разу. Например, конъюнкции  , , 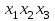 , 1 являются элементарными. Причем первая элементарная конъюнкция имеет ранг (число литералов) 2, вторая 3, а третья 0. , 1 являются элементарными. Причем первая элементарная конъюнкция имеет ранг (число литералов) 2, вторая 3, а третья 0.Следующие конъюнкции:  , , 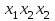 , ,  , , 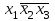 , 0 не являются элементарными. , 0 не являются элементарными.Определение. Элементарная конъюнкция булевой функции 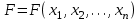 , содержащая n литералов, называется полной (или минтермом). , содержащая n литералов, называется полной (или минтермом).Определение. Дизъюнкция любого конечного множества элементарных конъюнкций булевой функции F называется дизъюнктивной нормальной формой (ДНФ) функции F. Число элементарных конъюнкций (слагаемых, термов), составляющих ДНФ, называется длиной ДНФ. Например, ДНФ  имеет длину, равную 3. имеет длину, равную 3.Для произвольной булевой функции F существует, вообще говоря, много различных реализующих ее ДНФ, отличающихся друг от друга длиной, числом вхождений литералов и т.д. Определение. Две (или несколько) ДНФ, реализующих одну и ту же булеву функцию F , называются эквивалентными (или равносильными). Например, для функции  , заданной булевым вектором w(F)=(00100111), существуют следующие эквивалентные ДНФ: , заданной булевым вектором w(F)=(00100111), существуют следующие эквивалентные ДНФ: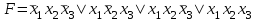 , (1) , (1) , (2) , (2) , (3) , (3)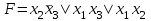 , (4) , (4) . (5) . (5)Определение. ДНФ булевой функции F, состоящая только из полных элементарных конъюнкций, называется совершеннойДНФ(СДНФ). Например, (1) СДНФ функции F. Отметим, что СДНФ является единственной (с точностью перестановки слагаемых) для конкретной булевой функции F . Любую булеву функцию F, заданную формулой, можно с помощью основныхравносильностей преобразовать к ДНФ, а затем к СДНФ. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Представление булевой функции в виде совершенной ДНФ и КНФ, минимальной КНФ, полинома Жегалкина Для булевой функции, заданной в виде ДНФ  , составить СДНФ и выполнить проверку по таблице истинности. , составить СДНФ и выполнить проверку по таблице истинности.Решение: Применяя закон склеивания (в обратном порядке:  ), дополняем конъюнкции, до полных элементарных конъюнкций. Конъюнкцию ), дополняем конъюнкции, до полных элементарных конъюнкций. Конъюнкцию 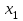 дополняем в два этапа, так как дополняем в два этапа, так как  не является элементарной конъюнкцией: не является элементарной конъюнкцией: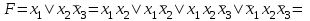 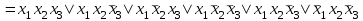 . .Так как 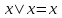 , после сокращения одинаковых конъюнкций получаем СДНФ: , после сокращения одинаковых конъюнкций получаем СДНФ: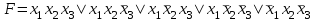 . .Таблица истинности СДНФ
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Определение.Полином булевой функции F, в слагаемые которого все переменные F входят только без отрицания или только с отрицанием, называется монотонно-поляризованным. Причем в первом случае полином функции F называется положительно-поляризованный и обозначается через P(F), а во втором случае - отрицательно-поляризованным и обозначается через Q(F). Полином P(F) иначе называется каноническим полиномом Жегалкина (или в зарубежной научно-технической литературе - формой Рида-Мюллера). Например, для булевой функции, заданной вектором значений таблицы истинности w(F)=(00100111) полиномы P(F) и Q(F) имеют вид: 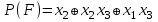 , ,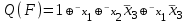 . .Отметим некоторые свойства монотонно-поляризованных полиномов P(F) и Q(F) булевой функции 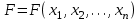 : :1. Полиномы P(F) и Q(F) являются для булевой функции F единственными. 2. Полиномы P(F) и Q(F) имеют степень n тогда и только тогда, когда таблица истинности функции F содержит нечетное число единиц. 3. Число слагаемых полинома P(F) (Q(F)) четно тогда и только тогда, когда  (соответственно (соответственно Понятие полноты множества функций. Замкнутые классы Определение. Множество 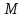 логических функций называется замкнутым классом, если любая суперпозиция функций из множества логических функций называется замкнутым классом, если любая суперпозиция функций из множества 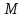 снова принадлежит снова принадлежит 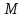 . .Всякая система  логических функций порождает некоторый замкнутый класс, а именно класс всех функций, которые можно получить суперпозициями функций логических функций порождает некоторый замкнутый класс, а именно класс всех функций, которые можно получить суперпозициями функций  . Такой класс называется замыканием . Такой класс называется замыканием  и обозначается и обозначается 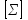 . Если множество . Если множество 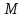 - функционально полная система, то - функционально полная система, то 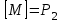 . . Теорема. Всякая булева формула, не содержащая отрицаний, представляет собой монотонную функцию отличную от константы; наоборот, для любой монотонной функции, отличной от 0 и 1, найдётся представляющая её булева формула без отрицаний. Из данной теоремы и того очевидного факта, что подстановка нескольких формул без отрицаний в формулу без отрицаний снова даёт формулу без отрицаний, вытекает следующая теорема. Теорема. Множество всех монотонных функций является замкнутым классом. Но поскольку всякая булева формула без отрицаний является суперпозицией дизъюнкций и конъюнкций, из данной теоремы непосредственно получаем следствие. Следствие. Класс монотонных функций является замыканием системы функций | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Проверка булевой функции на принадлежность к замкнутым классам, на полноту. Теорема. Если все функции функционально полной системы  представимы формулами над системой представимы формулами над системой  , то система , то система  также функционально полна. также функционально полна.Пример. а) Системы 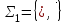 и и 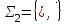 функционально полны. Действительно, с помощью законов Де Моргана и двойного отрицания можно выразить в каждой из этих систем функцию, недостающую до функционально полны. Действительно, с помощью законов Де Моргана и двойного отрицания можно выразить в каждой из этих систем функцию, недостающую до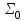 через остальные две: через остальные две: . .С точки зрения функциональной полноты систему 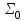 следует считать избыточной: она сохраняет свойство полноты и при удалении из неё конъюнкции или дизъюнкции. Однако легко видеть из приведённого примера, что, хотя системы следует считать избыточной: она сохраняет свойство полноты и при удалении из неё конъюнкции или дизъюнкции. Однако легко видеть из приведённого примера, что, хотя системы  и и 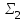 не являются избыточными, зато формулы в них получаются гораздо длиннее: замена одной операции на другую вносит в формулу сразу три лишних отрицания. не являются избыточными, зато формулы в них получаются гораздо длиннее: замена одной операции на другую вносит в формулу сразу три лишних отрицания.б) Системы  (штрих Шеффера) и (штрих Шеффера) и  (стрелка Пирса) являются функционально полными. (стрелка Пирса) являются функционально полными.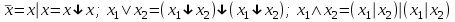 . .Таким образом, система 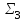 сводится к системе сводится к системе  , а система , а система 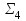 - к системе - к системе 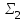 . .в) Система 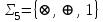 ( (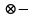 умножение по модулю 2, умножение по модулю 2,  сложение по модулю 2 – см. пункт 1 лекции № 8)) является функционально полной. Поскольку сложение по модулю 2 – см. пункт 1 лекции № 8)) является функционально полной. Поскольку 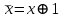 , данная система сводится к , данная система сводится к  . . | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Множества и подмножества. Понятие множество принадлежит к числу фундаментальных неопределяемых понятий математики. Множество можно представить себе как совокупность объектов, обладающих общим свойством. Объекты, из которых составлено множество, называются его элементами. Множества обычно обозначают большими латинскими буквами (например, A, S, D), а их элементы - строчными (например, a, s, d). Если элемент х принадлежит множеству А, то это обозначается: х  А; в противном случае говорят, что элемент не принадлежит множеству, это обозначается: х А; в противном случае говорят, что элемент не принадлежит множеству, это обозначается: х А. А.Примеры множеств. Множество N - множество натуральных чисел. 1  N. -1 N. -1 N. N.Множество L - множество букв русского алфавита.ф  L. v L. v L. L.Множество не содержащие элементов называется пустым. Это множество обозначается 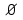 . .Множества можно задавать следующими способами. Перечисление элементов: P={точка, прямая, плоскость, тело}, S={0,1,2}. Задание характеристического свойства: L={n|n  N и n<7}. N и n<7}. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Операции над множествами Объединение двух множеств А и В – это новое множество, элементами которого являются элементы, принадлежащие множеству А или множеству В. Обозначение: А  В. В.А  В={x| х В={x| х А или х А или х В}. В}.Пересечение двух множеств А и В – это новое множество, элементами которого являются элементы, принадлежащие множеству А и множеству В. Обозначение: А  В. В.А  В={x| х В={x| х А и х А и х В}. В}.Разность двух множеств А и В – это новое множество, элементами которого являются элементы, принадлежащие множеству А и не принадлежащие множеству В. Обозначение: А \ В. А \ В={x| х  А и х А и х В}. В}.Обычно элементы множеств выбираются из некоторого достаточно широкого множества U, которое называется универсум. В связи с этим понятием можно ввести операцию дополнение. Дополнением множества А называется множества, которое состоит из элементов универсума, не принадлежащих множеству А. Обозначение: 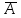 . .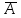 =U \ A или =U \ A или 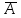 ={x| х ={x| х А и х А и х U}. U}. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Понятие предикат. Под предикатом предметной переменной х Например: Предикат х > 5, x Функция Р (х, у), где х, у Например: х<у | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Логические операции над предикатами. 1) Отрицание.  Рис. 1. Область истинности отрицания предиката 2) Конъюнкция Р (х) 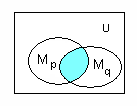 Рис. 2. Область истинности конъюнкция предикатов Дизъюнкция Р (х)  Рис. 3. Область истинности дизъюнкции предикатов ИмпликацияР (х)  Рис. 3. Область истинности импликаци предикатов Эквиваленция Р (х)  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Определение логического значения для высказываний Рассмотрим предложения: В любой треугольник можно вписать окружность. Всякое число, оканчивающееся на четную цифру, делится на 2. В этих предложениях встречаются слова «любой», «всякое». Эти слова заменяют специальным символом. Значок ( Например. Пусть Р (х) предикат, выражающий для х  N свойство быть простым числом. Тогда ( N свойство быть простым числом. Тогда ( N) Р (х) - ложное высказывание «любое натуральное число является простым». N) Р (х) - ложное высказывание «любое натуральное число является простым».Наряду с квантором всеобщности в логике предикатов рассматривается квантор существования: Его значок ( Например. Пусть Р (х) предикат, выражающий для х  N свойство быть простым числом. Тогда, ( N свойство быть простым числом. Тогда, ( N) Р (х) - истинное высказывание «существует натуральное число, которое является простым». N) Р (х) - истинное высказывание «существует натуральное число, которое является простым».Операция введения квантора называется операцией навешивания квантора. Навешивание квантора по какой-нибудь переменной понижает местность предиката. Переменная, по которой навешен квантор, называется связанной. Например.х<у - двухместный предикат. Навесим квантор: (  N) (х<у) предикат одноместный по переменной у. N) (х<у) предикат одноместный по переменной у.Таким образом, понизить местность предиката можно двумя способами. задать предметной переменной конкретное значение. навесить кванторы по одной или нескольким переменным. Квантор всеобщности можно рассматривать как обобщение конъюнкции для конечных и бесконечных множеств. Квантор существования можно рассматривать как обобщение дизъюнкции для конечных и бесконечных множеств. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Построение отрицаний к предикатам. Отрицание.  Область истинности отрицания предиката | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Понятие бинарного отношения и его свойства. |