Образовательная программа среднего профессионального образования Комплект контрольнооценочных средств по учебным
 Скачать 0.96 Mb. Скачать 0.96 Mb.
|
Отношения на множестве.Если в декартовом произведении в качестве множества В выбрать множество А ( то есть А Х А= А Для отношений на множестве вводятся понятия: Обратное отношение-это множество пар (а,b) таких, что (b,a) Дополнение-это множество пар (а,b) Тождественное отношение-множество пар (а, а) таких, что, а I= {(a, a), a Универсальное отношение U={(a,b),a Виды отношений:Инъекция. Е  сли каждый элемент множества А соответствует элементу из множества В, то отношение f называется инъективным. сли каждый элемент множества А соответствует элементу из множества В, то отношение f называется инъективным.Рис.2. Инъекция. Сюръекция. Если для каждого элемента y множества В существует элемент х 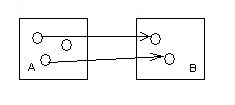 Рис.3.Сюръекция. Биекция. Если для каждого элемента y Биективное отношение инъективно и сюръективно. Биективное отношение имеет обратное отношение. 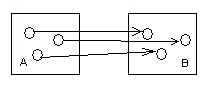 Рис.4. Биекция. | |||||||||||||||||||||||||||
| Отношение эквивалентности. Определение.Отношение называется отношением эквивалентности (или просто эквивалентностью), если оно рефлексивно, симметрично и транзитивно. Эта система обладает следующими свойствами: она образует разбиение множества 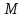 , то есть классы попарно не пересекаются; , то есть классы попарно не пересекаются;любые два элемента из одного класса эквивалентны; любые два элемента из разных классов не эквивалентны. Все эти свойства прямо следуют из определения отношения эквивалентности. | |||||||||||||||||||||||||||
| Исследование бинарных отношений на рефлексивность, симметричность и транзитивность; выделение классов эквивалентности Определение 1. Отношение 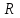 называется отношением нестрогого порядка, если оно является рефлексивным, антисимметричным и транзитивным. называется отношением нестрогого порядка, если оно является рефлексивным, антисимметричным и транзитивным.Определение 2. Отношение 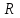 называется отношением строгого порядка, если оно является антирефлексивным, антисимметричным и транзитивным. называется отношением строгого порядка, если оно является антирефлексивным, антисимметричным и транзитивным.Оба типа отношений вместе называются отношениями порядка. Элементы 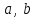 сравнимы по отношению порядка сравнимы по отношению порядка 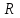 , если выполняется одно из двух отношений , если выполняется одно из двух отношений 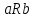 или или 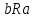 . Множество . Множество 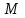 , на котором задано отношение порядка, называется полностью упорядоченным, если любые два его элемента сравнимы. В противном случае, множество называется частично упорядоченным. , на котором задано отношение порядка, называется полностью упорядоченным, если любые два его элемента сравнимы. В противном случае, множество называется частично упорядоченным. | |||||||||||||||||||||||||||
| Композиция отображений Определение.Пусть нам даны соответствия fÍАхВ, gÍCхD, то композицию соответствия gf будет представлять собой gfÍ АхD и действовать так: "аÎ А: (gf)(а)= g(f(а)) Пример. fÍRх[-1;1] gÍ [-1;2]х[-4;8] f(х)=sinх g(х)=4х Нужно построить gf и fg. gfÍRх[-4;8] fgÍ [-1;2]х[-1;1] 1) фиксируем элемент хR (gf)(х)= g(f(х))= 4sinх 2) фиксируем элемент х[-1;2] (fg)(х)=f(g(х))= 4sinх | |||||||||||||||||||||||||||
| Операции над подстановками Операция над (на) множеством M это функция [7]: 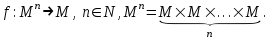 Из определения операции видно, что она замкнута на множестве М, т.е. результат операции не выходит за пределы этого множества. Еще одно свойство операции – однозначность результата, т.е. упорядоченный набор n элементов (операндов) дает в результате операции только один элемент. Порядок операции – это количество ее операндов: n = 1 соответствует унарной (монадической) операции, n = 2 – бинарной (диаедической) операции и т.д. Далее рассматриваются только бинарные операции. Они могут быть заданы в одной из трех форм: infix ( например, x + y); prefix ( +xy ); postfix ( xy+ ). Последние две формы дают бесскобочную запись (скобки вводятся, в инфиксной форме, для явного указания порядка выполнения операций). | |||||||||||||||||||||||||||
| Решение задач на запись циклического разложения подстановки Подстановка на множестве M – это биекция [7]:  MNn, n = |M| N. MNn, n = |M| N.В случае конечного множества M (как выше) количество подстановок определяется как количество перестановок из n элементов: 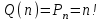 Можно считать, n ящиков заполняются объектами x1, …, xn, xiM. Поскольку MбиективноNn, можно определить подстановку как NnNn, т.е. иметь дело только с натуральными числами:  {i1, i2, … , in} = Nn. Обычно подстановка задается в форме стандартной таблицы, имеющей две строки. Верхняя строка всегда содержит последовательные натуральные числа, начиная с 1. В нижней строке, конечно, не должно быть повторений. Например:  Подстановка, как и любое бинарное отношение, может быть составной 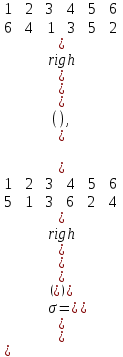  . .Видно, что в «контрпримере» 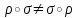 , т.е. «произведение» подстановок некоммутативно. , т.е. «произведение» подстановок некоммутативно.В составе любой подстановки можно выделить циклы. Их длина может составлять 1, 2,…, n. Цикл длины 1 – это фактически вырожденный цикл, стационарный элемент. | |||||||||||||||||||||||||||
| Выполнение операций и решение простейших уравнений в алгебре подстановок. 1: Коммутативность. x 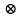 y = y y = y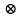 x, x, yM. x, x, yM. Например, на множестве целых чисел Zоперация сложения коммутативна – в отличие от операции вычитания. 2: Ассоциативност ь. (x 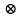 y) y) 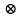 z = x z = x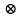 (y (y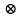 z), x, y, zM. z), x, y, zM.Фактически речь идет об изменении порядка действий (задаваемого скобками). Например, операция вычитания не ассоциативна. 3: Единица. l 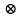 x = x, l, xM, l– леваяединица. x = x, l, xM, l– леваяединица.x 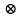 r = x, r, xM, r – правая единица. r = x, r, xM, r – правая единица. e 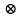 x = x x = x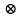 e = x, e, xM, е – двусторонняя или просто единица. e = x, e, xM, е – двусторонняя или просто единица. Например, сложение на множестве вещественных чисел Rимеет единицу (аддитивную): a + 0 = 0 + a = a. Вычитание имеет только правую единицу: a – 0 = a, но 0 – a a (если a 0). Единица операции умножения (типа умножения) – мультипликативная, обозначается обычно «1» . 4: Обратный элемент. х – левый обратный элемент по отношению к у, а у – правый по отношению х, если х у = е. «Просто» обратный элемент (взаимно обратные элементы), если х у = у х = е. Существование и единственность единицы и обратного элемента позволяет решать простейшие уравнения (п.4). 5: Идемпотентность. х х = х, х М. Вообще-то количество одинаковых элементов в выражении может быть любым. Идемпотентность позволяет в необходимых случаях сжимать или, наоборот, растягивать выражение. То же, кстати, было и в алгебре логике для операций дизъюнкция и конъюнкция. 6: Дистрибутивность. Здесь уже требуются две операции, обозначаемые, например, (операция типа умножение) и (операция типа сложение). Дистрибутивность по отношению к: х (у z) = (х у) (х z), (х у) z= (х z) (у z), x, y, zM. | |||||||||||||||||||||||||||
| Понятие вычета по модулю N. Операции над вычетами. Шифрование Вычетом числа a по модулюm называется остаток от деления a на m Из определения видно, что вычеты связаны с делением с остатком. Разделить натуральное число aна натуральное число b с остатком означает yнайти неотрицательные числа два числа qи г, причем г а = q·b + г | |||||||||||||||||||||||||||
| Метод математической индукции Метод математической индукции - не просто распространенный метод решения олимпиадных задач, но и способ доказательства многих утверждений в математической науке.1.)База индукции: первое утверждение ряда верно. 2.) Переход индукции: если верно какое-то утверждение ряда (неважно, какое именно), то верно и следующее за ним утверждение ряда. | |||||||||||||||||||||||||||
| Решение задач на выполнение операций в алгебре вычетов Для степени y=2n(n–натуральное число) установить классы сравнимости. Установить зависимость последней цифры этой степени от ее показателя. Решение и комментарии. Как известно, натуральные степени числа 2 оканчиваются цифрами {2, 4, 8, 6}. См. таблицу нескольких степеней числа 2. Определим функцию, которая ставит в соответствие каждому натуральному числу ппоследнюю цифру числа 2я:
Эта функция f(n) периодична с периодом 4. Это значит, что для целого числа k: f(n)=f(n+4)= f(n+4k),. Причем справедливы так же равенства: f(n)=f(n-4)= f(n-4k) Последнее равенство означают, что для любого пнужно найти минимальное натуральное т, такое, что f(m) = f(m + 4k) = f(n). Но это задача на делении с остатком числа n на 4: n=4k+m, k-частное, т - остаток. Очевидно, последняя цифра числа 2" зависит от остатка, полученного при делении показателя n степени 2 n на 4. Отразим этот факт в записи функции: f(n)= f(nmod 4) Из этой формулы можно установить, если f(nmod 4)=0, то  При делении чисел на 4 "nÎN, останки могут быть: 0,1,2,3. Таким образом, в частности, множество всех возможных показателей степени 2 n для любого n состоит из четырех подмножеств: 4k, 4k+ 1, 4k+ 2, 4k+3. | |||||||||||||||||||||||||||
| | |||||||||||||||||||||||||||
| Генерирование К-элементных подмножеств данного множества Для каждого сгенерированного элемента затем проверяются какие-то свойства для конкретной задачи. Задачи, в которых требуется определить количество возможных операций, называется комбинаторными. Пусть имеется группа некоторых объектов Из этой группы элементов будем образовывать подгруппы. Такие подгруппы будем называть соединениями. Из этих соединений выделим классы, которые будем называть размещениями. |
