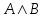Образовательная программа среднего профессионального образования Комплект контрольнооценочных средств по учебным
 Скачать 0.96 Mb. Скачать 0.96 Mb.
|
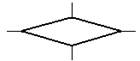
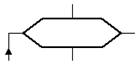
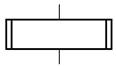
В городе Н от каждой площади отходит ровно 5 улиц, соединяющих площади. Докажите, что число площадей чётно, а число улиц кратно 5.Решение: По теореме, что число нечётных вершин любого графа чётно, следует, что число площадей (вершин графа) 2n, а число улиц (рёбер графа) будет (2n·5):2, а значит, число площадей чётно, а число улиц кратно 5. Задача № 24 Футбольный мяч сшит из 32 лоскутов: белых шестиугольников и чёрных пятиугольников. Каждый чёрный лоскут граничит только с белыми, а каждый белый – с тремя чёрными и тремя белыми. Сколько лоскутов белого цвета? Решение: Пусть на мяче число белых лоскутов х шт., а чёрных будет (32 – х) шт. Тогда границ белых лоскутов с чёрными 5(32-х)=3х, значит, х=20 и белых лоскутов 20 шт. Задача № 25 В государстве система авиалиний устроена таких образом, что любой город соединён авиалиниями не более чем с тремя другими и из любого города в любой другой можно проехать, сделав не более одной пересадки. Какое максимальное число городов может быть в этом государстве? Решение: Пусть существует некоторый город А. Из него можно добраться не более, чем до трёх городов, а из каждого из них ещё не более чем до двух (не считая А). Тогда всего городов не более 1+3+6=10. Значит всего городов не более 10. Пример на рисунке (его ещё называют графом Петерсона) показывает существование авиалиний. 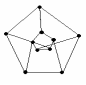 Задача № 26 Можно ли нарисовать графы изображенные на рисунках, не отрывая карандаш от бумаги и проводя каждое ребро ровно один раз? 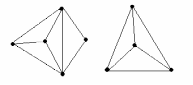 Решение: Можно, т. к. только 2 нечетные вершины. Нельзя, т. к. 4 нечетные вершины. Задача № 27 Доказать: (A®B, A® 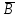 )Þ )Þ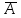 . .Доказательство:
Из определения следует, что противоречие логически влечет любую формулу, а тавтология логически следует из любой формулы логики. Определение. Формулы F и G называются равносильными, если они являются логическими следствиями друг друга. Обозначение: 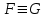 . .Проанализировав последнее определение, получаем, что формулы равносильны, если они на всех наборах значений переменных превращаются в одинаковые по истинностному значению высказывания. Задача № 28 Доказать закон отрицания конъюнкции ( 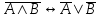 ) )Доказательство: Найдем значения для 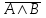 и и 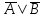 и сравним их. и сравним их.
Задача № 29 Найти значение 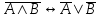 и убедиться, что при всех значениях A и B - это истинное значение. и убедиться, что при всех значениях A и B - это истинное значение.Решение:
Задача № 30 С помощью основных равносильностей доказать закон обобщенного склеивания 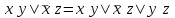 . .Решение. Применяя закон склеивания (в обратном порядке, то есть  ) и дистрибутивность (то есть вынесем за скобки ) и дистрибутивность (то есть вынесем за скобки 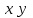 и и 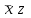 ), получим ), получим . .Задача № 31 Записать предложение: прямая а параллельна прямой b с помощью предиката. Решение: Предметная область – множество прямых. Введем предикат Р (х), х – прямая. Предикат параллельности х||у Тогда предложение можно записать в виде: Р (а) Задача № 32 Записать с помощью предиката: Аксиома: через две различные точки проходит единственная прямая. (Ели две точки принадлежат двум прямым, то эти прямые совпадают). Решение: Введем предикаты Т (х), х – точка; Р (х), х – прямая; J(x,y) - x Т (А) Задача № 33 Установить последнюю цифру степени y=2 2007 Решение. Имеем 2007=501·4+3, значит f (2007)=f (3)=23=8. Ответ: 8 5. Описание процедуры экзамена Комплексный экзамен по дисциплинам «Основы алгоритмизации и программирования» и «Дискретная математика» проводится в соответствии с расписанием по экзаменационным билетам, согласованным с ПЦК и утвержденным заместителем директора по КОД. Количество экзаменационных билетов превышает количество обучающихся. В билете – 2 теоретических вопроса и 1 практическое задание На подготовку к ответу обучающемуся отводится до 30 минут. Обучающийся предъявляет ответы в устной (письменной, смешанной) форме: устно раскрывает теоретические вопросы; решение задачи представляется в письменном виде с устными комментариями (пояснениями). Требования охраны труда: инструктаж по технике безопасности, правилам поведения на занятии, по соблюдению дисциплины, наличие инструктора (преподаватель). 6. Критерии оценки: Оценка "отлично" ставиться обучающемуся, обнаружившему всестороннее, систематическое и глубокое знание учебно-программного материала, умение свободно выполнять задания, предусмотренные программой, усвоившему основную литературу, рекомендованную программой, взаимосвязь основных понятий дисциплины в их значении для приобретаемой профессии, проявившему творческие способности в понимании, изложении и использовании учебно-программного материала. Оценка "хорошо" ставиться обучающему, показавшему полное знание учебно-программного материала, успешно выполняющему предусмотренные в программе задания, усвоившему основную литературу, рекомендованную в программе, показавшему систематический характер знаний по дисциплине и способному к их самостоятельному пополнению и обновлению в ходе дальнейшей учебной работы и профессиональной деятельности. Оценка "удовлетворительно" ставиться обучающему, показавшему знания основного учебно-программного материала в объеме, необходимом для дальнейшей учебы и предстоящей работы по специальности, справляющемуся с выполнением заданий, предусмотренных программой, знакомому с основной литературой, рекомендованной программой. Оценка "удовлетворительно" выставляется обучающемся, допустившим погрешности в ответе на экзамене и при выполнении экзаменационных заданий, но обладающим необходимыми знаниями для их устранения под руководством преподавателя. Оценка "неудовлетворительно" выставляется обучающемуся, обнаружившему пробелы в знаниях основного учебно-программного материала, допустившему принципиальные ошибки в выполнении предусмотренных программой заданий, оценка "неудовлетворительно" ставится обучающимся, которые не могут продолжить обучение или приступить к профессиональной деятельности по окончании колледжа без дополнительных занятий по соответствующей дисциплине. 7. Перечень материалов, оборудования и информационных источников, используемых при проведении промежуточной аттестации При проведении промежуточной аттестации обучающимся могут пользоваться конспектом лекций, ПК, справочными материалами. 8. Эталоны ответов на теоретические вопросы: Эталоны ответов на теоретические задания: по дисциплине «Основы алгоритмизации и программирования» Основные понятия алгоритмизации. Понятия «алгоритм», «исполнитель алгоритма». Алгори́тм — набор инструкций, описывающих порядок действий исполнителя для достижения результата решения задачи за конечное число действий. В старой трактовке вместо слова «порядок» использовалось слово «последовательность», но по мере развития параллельности в работе компьютеров слово «последовательность» стали заменять более общим словом «порядок». Это связано с тем, что работа каких-то инструкций алгоритма может быть зависима от других инструкций или результатов их работы. Таким образом, некоторые инструкции должны выполняться строго после завершения работы инструкций, от которых они зависят. Независимые инструкции или инструкции, ставшие независимыми из-за завершения работы инструкций, от которых они зависят, могут выполняться в произвольном порядке, параллельно или одновременно, если это позволяют используемые процессор и операционная система. Исполнитель алгоритма — это некоторая абстрактная или реальная (техническая, биологическая или биотехническая) система, способная выполнить действия, предписываемые алгоритмом. Свойства и формы записи алгоритмов. Основные свойства алгоритмов следующие: 1. Понятность для исполнителя — исполнитель алгоритма должен понимать, как его выполнять. Иными словами, имея алгоритм и произвольный вариант исходных данных, исполнитель должен знать, как надо действовать для выполнения этого алгоритма. 2. Дискpетность (прерывность, раздельность) — алгоpитм должен пpедставлять пpоцесс pешения задачи как последовательное выполнение пpостых (или pанее опpеделенных) шагов (этапов). 3. Опpеделенность — каждое пpавило алгоpитма должно быть четким, однозначным и не оставлять места для пpоизвола. Благодаpя этому свойству выполнение алгоpитма носит механический хаpактеp и не тpебует никаких дополнительных указаний или сведений о pешаемой задаче. 4. Pезультативность (или конечность) состоит в том, что за конечное число шагов алгоpитм либо должен пpиводить к pешению задачи, либо после конечного числа шагов останавливаться из-за невозможности получить решение с выдачей соответствующего сообщения, либо неограниченно продолжаться в течение времени, отведенного для исполнения алгоритма, с выдачей промежуточных результатов. Массовость означает, что алгоpитм pешения задачи pазpабатывается в общем виде, т.е. он должен быть пpименим для некотоpого класса задач, pазличающихся лишь исходными данными. Пpи этом исходные данные могут выбиpаться из некотоpой области, котоpая называется областью пpименимости алгоpитма. На практике наиболее распространены следующие формы представления алгоритмов: - словесная (запись на естественном языке); - графическая (изображения из графических символов); - псевдокоды (полуформализованные описания алгоритмов на условном алгоритмическом языке, включающие в себя как элементы языка программирования, так и фразы -естественного языка, общепринятые математические обозначения и др.); - программная (тексты на языках программирования). Основные алгоритмические конструкции: линейные, разветвляющиеся и циклические. 1.Базовая структура "следование". Образуется последовательностью действий, следующих одно за другим. 2.Базовая структура "ветвление". Обеспечивает в зависимости от результата проверки условия (да или нет) выбор одного из альтернативных путей работы алгоритма. Каждый из путей ведет к общему выходу, так что работа алгоритма будет продолжаться независимо от того, какой путь будет выбран. Структура ветвление существует в четырех основных вариантах: если—то; если—то—иначе; выбор; выбор—иначе. 3.Базовая структура "цикл". Обеспечивает многократное выполнение некоторой совокупности действий, которая называется телом цикла. Логические основы алгоритмизации. Основы алгебры логики. Алгеброй логики называется аппарат, который позволяет выполнять действия над высказываниями. Алгебру логику называют также алгеброй Буля, или булевой алгеброй, по имени английского математика Джорджа Буля, разработавшего в XIX веке ее основные положения. В булевой алгебре высказывания принято обозначать прописными латинскими буквами: A, B, X, Y. В алгебре Буля введены три основные логические операции с высказываниями? Сложение, умножение, отрицание. Определены аксиомы (законы) алгебры логики для выполнения этих операций. Действия, которые производятся над высказываниями, записываются в виде логических выражений. Логические операции: конъюнкция, дизъюнкция, инверсия, импликация, эквиваленция. Операция И — логическое умножение (конъюнкция) Логическая операция И выполняет функцию пересечения двух высказываний (аргументов), в качестве которых может быть и простое, и сложное логическое выражение. Результатом операции И является выражение, которое будет истинным тогда и только тогда, когда истинны оба исходных выражения. Операция ИЛИ — логическое сложение (дизъюнкция, объединение) Логическая операция ИЛИ выполняет функцию объединения двух высказываний, в качестве которых может быть и простое, и сложное логическое выражение. Высказывания, являющиеся исходными для логической операции, называют аргументами. Результатом операции ИЛИ является выражение, которое бу¬дет истинным тогда и только тогда, когда истинно будет хотя бы одно из исходных выражений. Операция НЕ — логическое отрицание (инверсия) Логическая операция НЕ применяется к одному аргументу, в качестве которого может быть и простое, и сложное логическое выражение. Операция «ЕСЛИ-ТО» — логическое следование (импликация) Эта операция связывает два простых логических выражения, из которых первое является условием, а второе — следствием из этого условия. Операция «А тогда и только тогда, когда В» (эквивалентность, равнозначность) Результат операции эквивалентность истинен только тогда, когда А и В одновременно истинны или одновременно ложны. Законы алгебры логики. 1. Закон одинарных элементов 2. Законы отрицания a. Закон дополнительных элементов b. Двойное отрицание c. Закон отрицательной логики 3. Комбинационные законы a. закон тавтологии (многократное повторение) b. закон переместительности c. закон сочетательности d. закон распределительности 4. Правило поглощения (одна переменная поглощает другие) 5. Правило склеивания (выполняется только по одной переменной) Таблицы истинности. Таблица истинности — это таблица, описывающая логическую функцию. Под «логической функцией» в данном случае понимается функция, у которой значения переменных (параметров функции) и значение самой функции выражают логическую истинность. Например, в двузначной логике они могут принимать значения «истина» либо «ложь».
Составление таблиц истинности для сложных логических функций. Алгоритм построения таблиц истинности для сложных выражений: Определить количество строк: количество строк = 2n + строка для заголовка, n - количество простых высказываний. Определить количество столбцов: количество столбцов = количество переменных + количество логических операций; определить количество переменных (простых выражений); определить количество логических операций и последовательность их выполнения. 3. Заполнить столбцы результатами выполнения логических операций в обозначенной последовательности с учетом таблиц истинности основных логических операций. Составление блок-схем алгоритмов. Блок-схемой называют графическое представление алгоритма, в котором он изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. В блок-схеме каждому типу действий (вводу исходных данных, вычислению значений выражений, проверке условий, управлению повторением действий, окончанию обработки и т.п.) соответствует геометрическая фигура, представленная в виде блочного символа. Блочные символы соединяются линиями переходов, определяющими очередность выполнения действий. Приведем наиболее часто употребляемые символы.
|