|
|
Образовательная программа среднего профессионального образования Комплект контрольнооценочных средств по учебным
Размещения.
Размещениями из m-элементов по n называются соединения, каждое из которых содержит n элементов, взятых из данных m и которые отличаются друг от друга или элементами, или их порядком.
Предполагается, что элементы водном размещении не повторяются.
|
Понятие графа. Способы задания графа. Методика выделения компонента
связности в графе
Графом G(V,E) называется совокупность двух множеств - непустого множества V (множества вершин) и множества Е неупорядоченных пар различных элементов множества V (Е - множество ребер).
G(V,E): 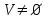 , E , E VxV. VxV.
Число вершин графа G обозначим р, а число ребер – q.
р(G) = |V| q(G) = |E|.
Часто рассматриваются следующие родственные графам объекты.
1. Если элементами множества Е являются упорядоченные пары, то граф называется ориентированным (или орграфом). В этом случае элементы множества V называются узлами, а элементы множества  - дугами (G(V, - дугами (G(V,  )). )).
2. Если элементом множества Е может быть пара одинаковых (не различных) элементов V, то такой элемент множества Е называется петлей, а граф называется графом с петлями (или псевдографом).
3. Если Е является не множеством, а набором, содержащим несколько одинаковых элементов, то эти элементы называются кратными ребрами, а граф называется мультиграфом.
Далее выражение: граф G(V,E) означает неориентированный граф без петель и кратных ребер.
Обычно граф изображают диаграммой: вершины - точками (или кружками), ребра - линиями.
|
Распознавание мостов и разделяющих вершин в графе
1.  . . 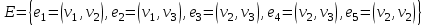 . .
Т.о. это неориентированный граф с петлей и кратными ребрами.
2
. 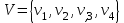 . . 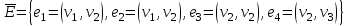 . .
Рис. 1. Неориентированный граф с петлей и кратными ребрами.
Т.о. это ориентированный граф с петлей и кратными ребрами.

Рис. 2. Ориентированный граф с петлей и кратными ребрами.
3
.  . . 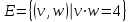 , т.о. , т.о. 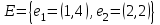
|
Нахождение расстояния между вершинами в графе.
Пусть v1, v2 - вершины, е = (v1, v2) - соединяющее их ребро. Тогда вершина v1 и ребро е инцидентны, вершина v2 и ребро е также инцидентны. Два ребра, инцидентные одной вершине, называются смежными; две вершины, инцидентные одному ребру, также называются смежными.
Степенью вершины v графа G(V,E) называется число ребер, инцидентных данной вершине. Обозначение: 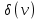 . .
Вершина, имеющая степень 0 называется изолированной, имеющая степень 1 – висячей.
|
|
Изоморфные графы. Эйлеровы графы
Изоморфизм графов
Говорят, что два графа G1(V1,E1) и G2(V2,E2) изоморфны (обозначается G1 G2), если существует биекция h: V1 V2, сохраняющая смежность. V2, сохраняющая смежность.
Графы рассматриваются с точностью до изоморфизма.
Пример
Три внешне различные диаграммы, приведенные на рис. 1, являются диаграммами одного и того же графа К3,3.
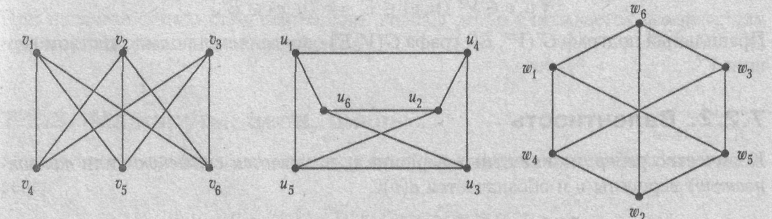
Рис. 1. Диаграммы изоморфных графов
Числовая характеристика, одинаковая для всех изоморфных графов, называется инвариантом графа. Так, p(G) и q(G) - инварианты графа G.
Не известно никакого набора инвариантов, определяющих граф с точностью до изоморфизма.
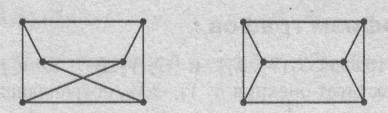
Цикл, содержащий каждое ребро ровно один раз, называется эйлеровым. Граф, содержащий эйлеровый цикл, называется эйлеровым графом.
|
|
Плоские графы. Деревья и их свойства
Деревом называется связный граф, не содержащий циклов. Любой граф без циклов называется ациклическим (или лесом). Таким образом, компонентами леса являются деревья. На рисунке 1 изображены все деревья шестого порядка.
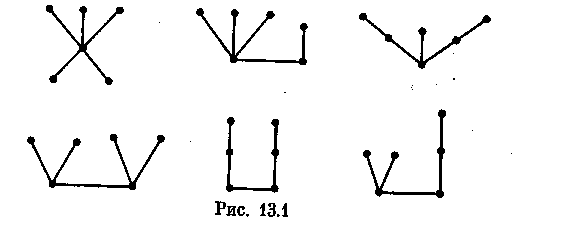
|
Проверка графа на плоскость.
|
Матрицей смежностей А(D) орграфа D называется (р×р)-матрица ||aij||, у которой aij= 1, если ViVj- дуга орграфа D, и aij=0 в противном случае. Матрица смежностей которого имеет вид (рис. 6):
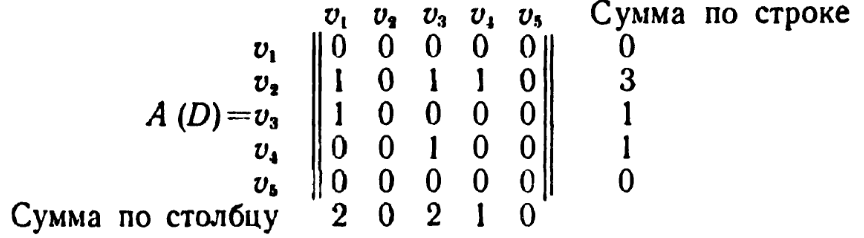
Матрица смежности графа
Легко проверить, что суммы элементов по строкам матрицы A(D) равны полустепеням исхода вершин орграфа D, а суммы элементов по столбцам - полустепеням захода.
Как и в случае графов, степени матрицы смежностей А орграфа дают полную информацию о числе маршрутов, идущих из одной вершины в другую. Теорема. (i, j)-й элемент аijn матрицы А" равен числу маршрутов длины n, идущих из вершины vi в вершину vj.
8. ПРИЛОЖЕНИЕ-ВАРИАНТЫ БИЛЕТОВ
|
|
|
 Скачать 0.96 Mb.
Скачать 0.96 Mb.

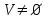 , E
, E VxV.
VxV.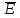 - дугами (G(V,
- дугами (G(V, 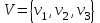 .
. 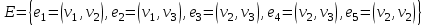 .
.
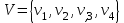 .
. 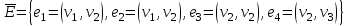 .
.

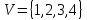 .
. 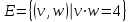 , т.о.
, т.о. 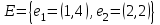
 .
. V2, сохраняющая смежность.
V2, сохраняющая смежность.

