Р.Т. Часть 1. Механика и молекулярная физика. Общая физика механика и
 Скачать 1.27 Mb.
|
|
Графическое представление результатов измерений Результаты экспериментальных исследований целесообразно представлять в виде графика зависимости одной измеряемой величины от другой. Сопоставляя найденные экспериментально точки с теоретической кривой, можно судить о том, согласуются ли результаты опыта с ожидаемыми закономерностями, а во многих случаях и с ожидаемой величиной, получаемой из зависимости между измеряемыми величинами. Особенно удобно проверить, укладываются ли данные экспериментальные точки на прямую линию. Поэтому при построении графиков желательно выбирать такие координаты, при которых ожидаемая зависимость была бы линейной. Такие графики (зависимости) называются линеаризованными. Например, при определении ускорения свободного падения из соотношения h = gt2 /2 между высотой h и временем падения тела tудобно строить линеаризованный график в координатах у = h и х = t2, Однако при построении графика, как правило, обнаруживается, что экспериментальные точки не укладываются на ожидаемую прямую. Такой разброс точек обусловлен погрешностями измерений физических величин. В этом случае необходимо построить доверительные интервалы для каждой из экспериментальных точек. Графически доверительный интервал для физической величины х представляет собой отрезок, расположенный вдоль оси х, ширина которого равна удвоенной абсолютной суммарной погрешности σ(х) величины х и в центре которого находится данная экспериментальная точка. После того, как на графике будут изображены доверительные интервалы для экспериментальных точек, следует провести прямую таким образом, чтобы она прошла внутри всех доверительных интервалов (рис. 1.). Если это удалось сделать, то может представлять интерес такая характеристика прямой линии, как её угловой коэффициент. Р 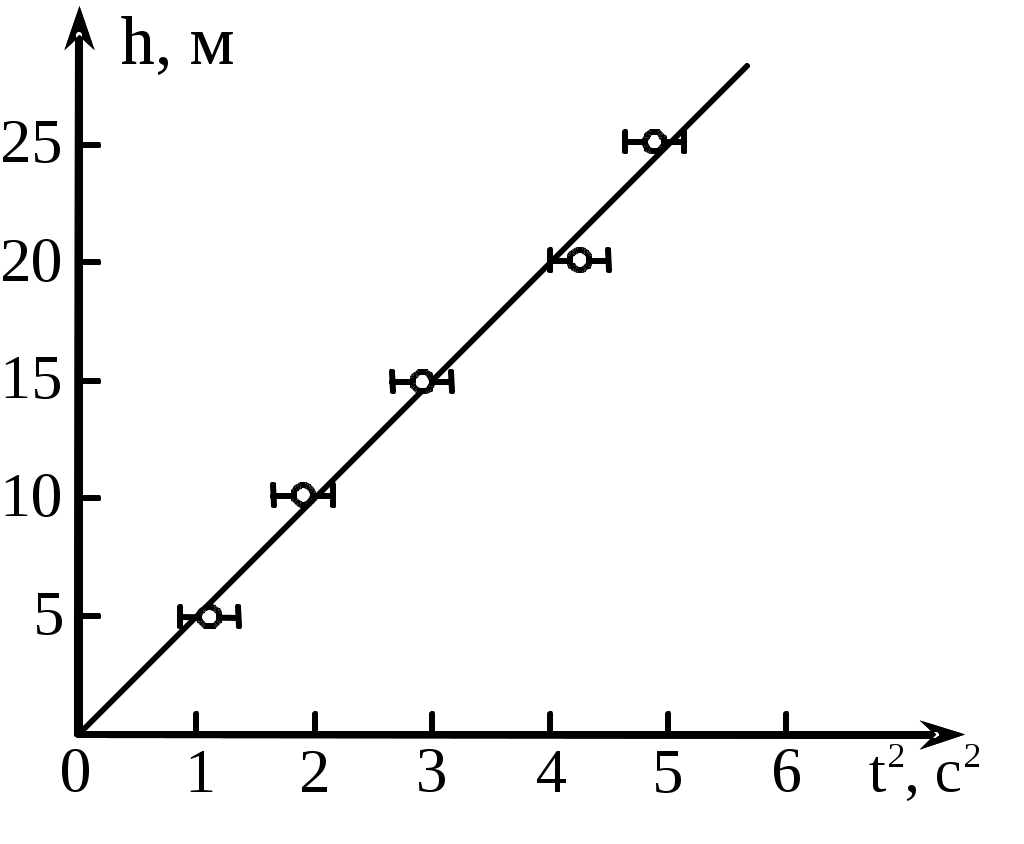 ис.1. Зависимость высоты падения h от квадрата времени падения В уравнении прямой у = ax + b, построенной в осях (у, х), параметр а является угловым коэффициентом, а параметр b – свободным членом линейной функции. Графически угловой коэффициент можно найти как отношение произвольного приращения  вдоль оси у к соответствующему приращению  вдоль оси х, определяемому из линейного графика:  . Важно, чтобы величины отрезков  и были найдены с учетом масштаба, откладываемого вдоль соответствующих осей графика. Обычно угловой коэффициент линеаризованной зависимости связан с какой-либо физической величиной, которую нетрудно найти. Например, в рассматриваемом примере (рис. 6.1.) по угловому коэффициенту прямой (т.е. по совокупности всех результатов измерений) можно определить величину ускорения свободного падения: Следует учитывать, что угловой коэффициент может иметь различный знак в зависимости от ориентации прямой в выбранной системе отчета. Это следует из того, что если (х1, у1) и (x2, y2) –координаты каких-либо двух точек на прямой у = f(х), то угловой коэффициент записывается в следующем виде: а = (у2 – y1)/(x2 – х1). Метод наименьших квадратов Рассматриваемый метод позволяет рассчитать параметры а и b линеаризованного графика у = f(x) еще до его построения. Для этого достаточно располагать массивами измеренных величин  и  Расчет производится по формулам: ;  ,куда входят следующие величины:       Суммирование в последних выражениях проводится по всем экспериментальным точкам. Чтобы по известным значениям величин а и b построить прямую, нужно задаться произвольными значениями хN и хM абcцисс двух точек N и М, а затем по формулам  и  вычислить соответствующие им ординаты. Поставив на график две точки с координатами (xN, уN) и (хM, уM), без труда можно провести через них единственную прямую.Лабораторная работа0.0 Определение ускорения свободного падения методом математического маятника. Цель работы:Определение ускорения свободного падения с помощью математического маятника.  -период колебаний математического маятника; -приведенный период; -среднее значение ускорения свободного падения;Принимаем:  -стандартная (средняя квадратичная) погрешность; -относительная погрешность определения g; - абсолютная погрешность определения g;где, l - длинанити маятника;  - абсолютная погрешность измерения длины нити маятника; -среднее значение приведенного периода.Таблица определения ускорения свободного падения аналитическим способом:
Определение ускорения свободного падения графическим способом:
|
