Р.Т. Часть 1. Механика и молекулярная физика. Общая физика механика и
 Скачать 1.27 Mb.
|
|
Методика эксперимента С помощью штангенциркуля измерьте диаметры валика, диска–маховика и сменных колец (dв = 2r, D = 2R, Dki = 2Rki, i – номер сменного кольца); каждый диаметр должен измеряться в трех различных сечениях. Полученные значения и указанные на частях маятника (валик, диск – маховик, сменные кольца) значения их масс (mв, mд, mк) внесите в табл.1 Подготовьте установку к работе, для чего: выровняйте установку по высоте и горизонтали с помощью ножек; укрепите на диске-маховике маятника одно из сменных колец (при смене колец убедитесь в том, что кольцо насажено на диск до упора); при необходимости установите с помощью воротка необходимую длину бифилярного подвеса, соответствующую высоте h падения маятника, определяемой по шкале на стойке; включите шнур питания в сеть и, нажав кнопку «Сеть», убедитесь в исправности электросхемы установки (должны загореться лампочки фотоэлектрических датчиков и цифровые индикаторы миллисекундомера; при нажатии кнопки «Сброс» на индикаторах должны устанавливаться нули; при подъеме маятника в верхнее положение он должен там фиксироваться с помощью электромагнита на верхнем кронштейне) проведите пробный пуск установки, нажав на кнопку «Пуск»; убедитесь в исправности работы миллисекундомера и фотоэлектрических датчиков по показаниям индикаторов миллисекундомера, отсчитывающего время t падения маятника. Отсчет времени должен заканчиваться при достижении падающим вниз маятником нижнего положения. При необходимости сместите по высоте нижний кронштейн, с помощью которого определяется высота h падения маятника. Снимите с диска-маховика сменное кольцо и проведите 5 пусков маятника без сменных колец. Результаты измерения времени t0 занесите в табл.2 . В той же таблице укажите высоту h падения маятника. Установите на диск-маховик одно из сменных колец (обозначьте его номером один) и вновь проведите 3-5 пусков маятника. Результаты измерения времени t1 так же занесите в таблицу 2. Смените кольцо на диске-маховике, проведите 3-5 пусков маятника с кольцом номер 2, результаты измерения времени t2 внесите в табл.2. Если будет указано преподавателем, проведите аналогично пятикратный пуск маятника со сменным кольцом номер три; результаты измерения времени t3 внесите в табл.2. Отключите установку от сети, приведите установку в исходное состояние. Измерения. Обработка результатовизмерений По результатам прямых измерений диаметров различных частей маятника (см. табл. 1) вычислите среднее значения этих диаметров и внесите в табл.1. На основе формул (6) и (7) получите и внесите в табл.1 теоретические значения моментов инерции, указанных в табл.1; при расчетах учтите изменения в формулах, связанные с использованием диаметров (а не радиусов). Найдите средние значения времен падения маятника (см. табл. 2, 3-я графа снизу), по формуле (5) найдите экспериментальные значения моментов инерции (см. табл.2, 2-я графа снизу), оцените абсолютную и относительную погрешности определения одного (любого) из этих моментов по экспериментальным данным и запишите их в самой нижней графе табл.2. Полный расчет погрешностей приведите в отчете (сразу после табл. 2). __________________________________________________________________________ __________________________________________________________________________ __________________________________________________________________________ __________________________________________________________________________ __________________________________________________________________________ Составьте теоретически и экспериментально определенные моменты инерции. Проанализируйте возможные источники расхождения между этими величинами, результаты анализа приведите в отчете. Таблица 1
Таблица 2
Расчет относительной погрешности измерений для Δm=0,5 г., Δr=0,005 мм., Δh=1 мм., <Δt > по формуле  :__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ Вывод:__________________________________________________________________ ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ Контрольные вопросы Поясните способы измерения времени t и высоты h падения маятника. _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ Объясните, как установить нижний кронштейн 5, чтобы правильно измерить время t падения маятника. ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ Укажите условия, при которых справедливо пренебрежение толщиной нитей, наматываемых на валик маятника. Рассмотрите изменения в расчетных формулах, если эти условия не выполняются. ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ Что такое плоско – параллельное движение твердого тела, какими уравнениями оно описывается (второй закон Ньютона)? ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ Приведите формулы связи линейных и угловых характеристик плоско – параллельного движения. ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ Выведите формулы определения моментов инерции диска и кольца. _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ Покажите преимущества выбора оси, проходящей через центр масс, для описания вращательной составляющей плоского движения. ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ Объясните, почему маятник после достижения нижнего положения поднимается. Сравните ускорения маятника и натяжения нитей при движении маятника вниз вверх. ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ Оценить расхождение между  и  . Чем оно обусловлено.___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ Сформулируйте закон сохранения момента импульса, энергии. ___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ Ответы на вопросы преподавателя (по выбору): Лабораторная работа 2.1 Определение постоянной Больцмана Допуск____________________________________________________ Отработка_______________________________________________ Защита___________________________________________________ Цель работы: определить постоянную Больцмана из основного уравнения кинетической теории газов Приборы и принадлежности: лабораторная установка, манометр, термометр, медицинский шприц Теоретическое введение Постоянная Больцмана является одной из фундаментальных физических постоянных. Она входит во многие важнейшие соотношения физики: в основное уравнение молекулярно-кинетической теории, в уравнение состояния идеального газа, в выражение для средней энергии теплового движения частиц, во все уравнения, которые содержат классические или квантовые функции распределения частиц по энергиям. Постоянная Больцмана связывает энтропию физической системы с термодинамической вероятностью ее состояния. Эту величину ввел М. Планк и определил ее как отношение универсальной (молярной) газовой постоянной R и постоянной Авогадро NA:  .Ч  тобы выяснить физической смысл постоянной Больцмана, надо обратиться к выражению 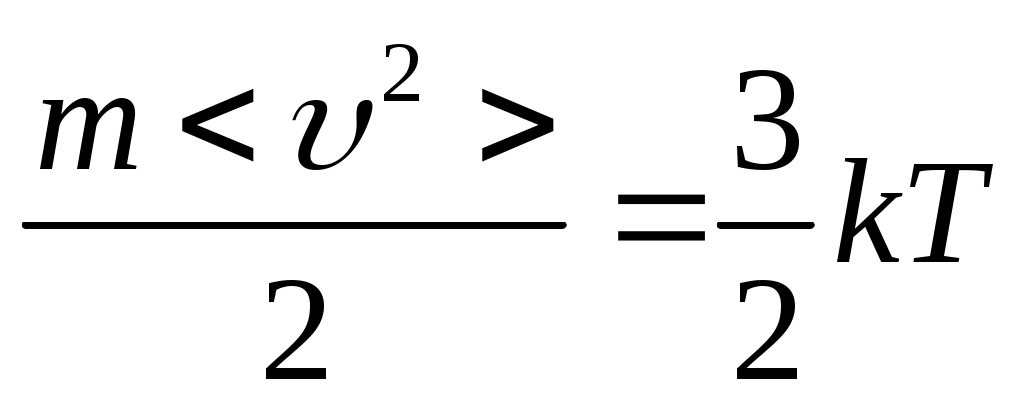 : она равна изменению среднего значения кинетической энергии молекул при изменении температуры на один кельвин.Значение постоянной k было определенно в многочисленных опытах Ж.Перрена, посвященных проверке распределения Больцмана. На основе данных об универсальной газовой постоянной R и постоянной Авогадро NA получено значение k = 1,380662∙10-23 Дж/К. Экспериментальная установка (рис.1) Стеклянный сосуд (1) плотно закрыт пробкой. Через пробку пропущена металлическая трубка, соединенная гибким шлангом с жидкостным манометром (2). В пробку герметично введена медицинская игла, соединенная со шприцом (3). С помощью шприца можно вводить в сосуд дозированный объем легко испаряющихся веществ. Методика и техника эксперимента Если в сосуд ввести небольшое количество этилового спирта, то вследствие испарения образуется газообразный спирт, к которому приближенно применимы законы идеального газа. При этом давление в сосуде увеличивается на некоторую величину р. Ее можно измерить с помощью манометра. Связь между давлением и концентрацией молекул при постоянной температуре газа выражается основным уравнением кинетической теории. До введения спирта  ,где р1 – первоначальное давление воздуха в сосуде, n1 – концентрация молекул воздуха, Т – температура воздуха. После введения спирта:  .Разность р2 – р1 представляет собой парциальное давление газообразного спирта:  . (1)Здесь n2 – n1 = n – концентрация молекул спирта. Ее можно найти, воспользовавшись выражением  , где V – объем сосуда,  − число молекул спирта в сосуде.Отсюда:  (2)Уравнение (1) принимает вид  (3)Экспериментально величина p определяется с помощью жидкостного манометра и вычисляется по следующей формуле:  , (4)где h – разность уровней жидкости между левым и правым коленом манометра (м); ρв – плотность воды. С учетом этого формула (3) принимает вид:  (5)Отсюда:  (6)При расчете принять: ρв=103 кг/м3, g=9,81 м/с2, V=5.10-3 м3, NA=6,022,1023 моль-1, ρсп=0,8,103 кг/м3, Мсп=46,10-3 кг/моль. Величины Т, h, Vсп – определяются экспериментально. Таким образом, для определения постоянной Больцмана необходимо выполнить следующие действия: Убедиться, что давление в сосуде равно атмосферному (уровни жидкости в коленах манометра одинаковы). Набрать в шприц не более 0,4 мл спирта, вставить шприц в основание иглы и ввести спирт внутрь сосуда. Внимание! Не следует в ходе эксперимента вынимать шприц из иглы, иначе герметичность сосуда будет нарушена. Время испарения спирта – 30-40 мин. Измерить жидкостным манометром парциальное давление газообразного спирта. Определить температуру в помещении По формуле (6) рассчитать постоянную Больцмана. Контрольные вопросы Каков физический смысл постоянной Больцмана? ____________________________________________________________________________________________________________________________________________ Почему газообразный спирт в сосуде можно приближенно считать идеальным газом? ____________________________________________________________________________________________________________________________________________ Почему температуру газа в сосуде можно считать неизменной, ведь при испарении температура должна понижаться? ____________________________________________________________________________________________________________________________________________ Каким образом можно повысить точность определения постоянной Больцмана? ____________________________________________________________________________________________________________________________________________ Лабораторная работа 2.4. Определение показателя адиабаты для воздуха методом Клемана-Дезорма Допуск____________________________________________________ Отработка_______________________________________________ Защита___________________________________________________ Цель работы: определение отношения теплоемкости воздуха при постоянном давлении к теплоемкости воздуха при постоянном объеме методом Клемана-Дезорма. Приборы и принадлежности: устройство, включающееся в себя стеклянный баллон, насос (компрессор), кран, соединенный с U-образным манометром. Краткое теоретическое введение Теплоемкостью тела называется физическая величина, равная отношению количества теплоты  , сообщаемой телу, к изменению его температуры в рассматриваемом термодинамическом процессе: . (1)Теплоемкость тела зависит от его массы, химического состава и вида процесса, при котором осуществляется передача тепла . Теплоемкость единицы массы тела называется удельной теплоемкостью , (2)где m – масса тела. Теплоемкость одного моля вещества называют молярной теплоемкостью  , (3)где – молярная масса. Газы по сравнению с веществами в жидком и твердом состоянии обладают большим коэффициентом объемного расширения. Потому теплоемкость газов сv при постоянном объеме отличается значительно от теплоемкости сV при постоянном давлении, причем  .Действительно, если нагревать газ при постоянном объеме, то все количество теплоты, сообщаемое ему, идет на увеличение внутренней энергии. Если нагревать газ при постоянном давлении, то тепло расходуется не только на увеличение внутренней энергии, но и на работу изобарного расширения. Для идеального газа разность молярных теплоемкостей равна универсальной газовой постоянной R (уравнение Майера):  . (4)В данной работе определяется важная термодинамическая величина  , называемая показателем адиабаты, кривой, графически изображающей адиабатический процесс.Адиабатическим называется термодинамический процесс, происходящий без теплообмена с окружающей средой (  ). Связь между параметрами, определяющими состояние идеального газа, находится из первого закона термодинамики с использованием уравнения Менделеева-Клапейрона и Майера. Уравнения, связывающие параметры газа при адиабатическом процессе, называются уравнениями адиабаты, или уравнениями Пуассона. Эти уравнения имеют вид: ; (5) ; (6) . (7)Так как > 1, то из (6) следует, что при адиабатическом расширении газ охлаждается, при адиабатическом сжатии – нагревается. Это явление находит применение в дизелях, где воспламенение рабочей смеси осуществляется путем адиабатического сжатия. Метод измерений Метод определения , используемый в данной работе, был предложен в 1919 г. Клеманом и Дезормом. Он основан на исследовании некоторой массы газа, последовательно проходящего через три состояния. О  бщая схема установки представлена на рис. 1. При помощи насоса воздух накачивается в большой стеклянный баллон 3 до некоторого давления р1, превышающего атмосферное: ,где Н – атмосферное давление, h1 – избыток давления сверх атмосферного (измеряется водяным манометром 1). Когда воздух в баллоне примет температуру окружающего воздуха, быстро открывается кран К2 и воздух выпускается наружу до тех пор, пока давление в баллоне не станет равным атмосферному. Выход воздуха происходит быстро, поэтому передачей тепла через стеклянные стенки баллона можно пренебречь и процесс расширения воздуха в баллоне считать адиабатическим. При этом расширяющийся воздух совершает работу против внешних сил – сил давления атмосферы. Следовательно, температура воздуха в баллоне понизится. Если теперь закрыть кран К2 и дать воздуху в баллоне нагреться до температуры окружающего воздуха, то его давление возрастет до некоторой величины  ,где h2 – избыток давления над атмосферным. И 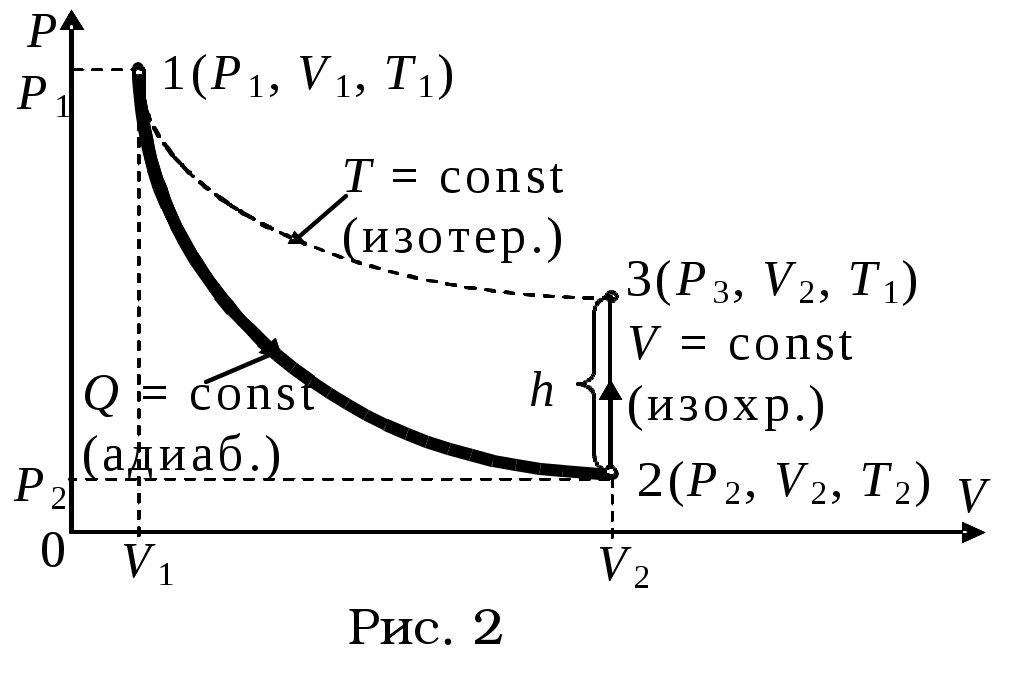 з полученных трех состояний воздуха в баллоне несложно рассчитать коэффициент Пуассона. Выделим мысленно некоторую массу т воздуха, которая остается в баллоне в течение всего эксперимента. Рассмотрим три состояния этой массы, представляя соответствующие им параметры газа (рис. 2). Таблица 1
Сопоставляя 1-е и 3-е состояния (1 и 3 строка табл. 1), видим, что температура воздуха, занимающего объемы V1 и V2, одинакова. Согласно закону Бойля-Мариотта, имеем  ,или  . (8)Сравнивая 1-е и 2-е состояния, видим, что здесь произошло адиабатическое расширение газа. Согласно уравнению Пуассона, получим:  , . (9)Из (8) и (9) следует: 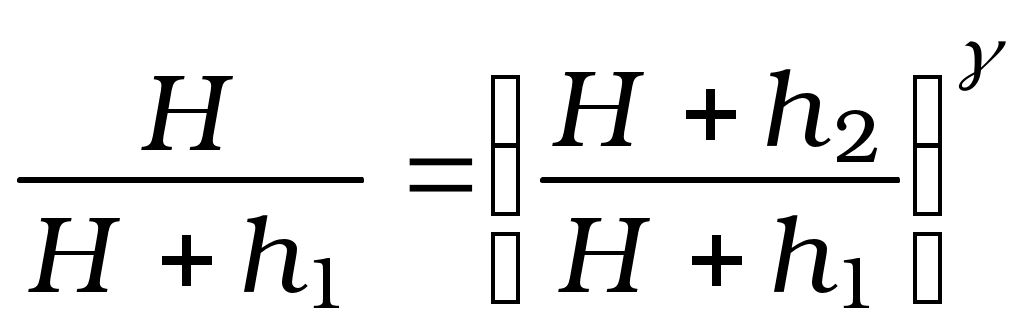 .Логарифмирование дает  .Так как давления Н, Н + h1 и Н + h2 незначительно отличаются друг от друга, то в первом приближении логарифмы величин можно заменить их численными значениями. В таком случае  ,т.е. искомая величина (экспериментальная)  . (10)К тому же результату можно прийти и в том случае, если полагать, что воздух в сосуде 3 сначала не нагнетается, а разрежается. Когда сосуд на короткое время сообщается с атмосферой, в нем происходит адиабатическое сжатие воздуха и температура последнего повышается доT2, после чего происходит выравнивание ее с температурой окружающего воздуха. В остальном рассуждения остаются теми же. Описание экспериментальной установки Э  кспериментальная установка представлена на рис. 3.На передней панели расположены: U-манометр (1) с измерительной линейкой (2), кран К1 напуска воздуха (3), клапан К2 сброса давления (4), пневмопровод (5) и тумблер включения микрокомпрессора «Компрессор» (6) с индикацией включения (7). U-образный манометр имеет переливной бачок (9). Установка содержит стеклянный баллон (8), наполняемый воздухом. Баллон (8) соединен с водяным U-манометром (1) и компрессором с помощью пневмопровода. Быстрое изменение давления в баллоне происходит практически без теплообмена с окружающей средой. Поэтому процесс, происходящий при открывании клапана (4), с достаточной точностью можно считать адиабатным. Порядок выполнения работы Включить электропитание установки. Записать в табл. 2 начальный уровень h0 (левый и правый уровни в манометре одинаковые). Включить электропитание компрессора. Открыть кран К1 и накачать в баллон воздух так, чтобы разность уровней жидкости в манометре была равна 250 – 300 мм. Примечание: накачивать воздух в баллон нужно медленно (чтобы избежать значительного повышения температуры воздуха в баллоне) и осторожно (чтобы нижний уровень жидкости не достиг колена манометра). Закройте кран К1, выждать 2-3 минуты до тех пор пока температура воздуха в баллоне не станет равной температуре окружающей среды. После чего записать начальную разность уровней h1 в таблицу 2. Примечание: в дальнейших опытах начальную разность уровней необходимо поддерживать постоянной. Резко нажать на клапан К2, соединив баллон с атмосферой и дождавшись когда уровень дойдет до h0, закрыть клапан. Через 3 – 4 минуты (после того, как уровни жидкости в манометре стабилизируются) записать разность значений уровней жидкости h2 в таблицу 2. Повторить опыты (пункты с 3 по 7) пять раз. Результаты измерений записать в таблицу 2. Вычислить  по формуле (10) и определить  Определить относительную погрешность измерения  , где 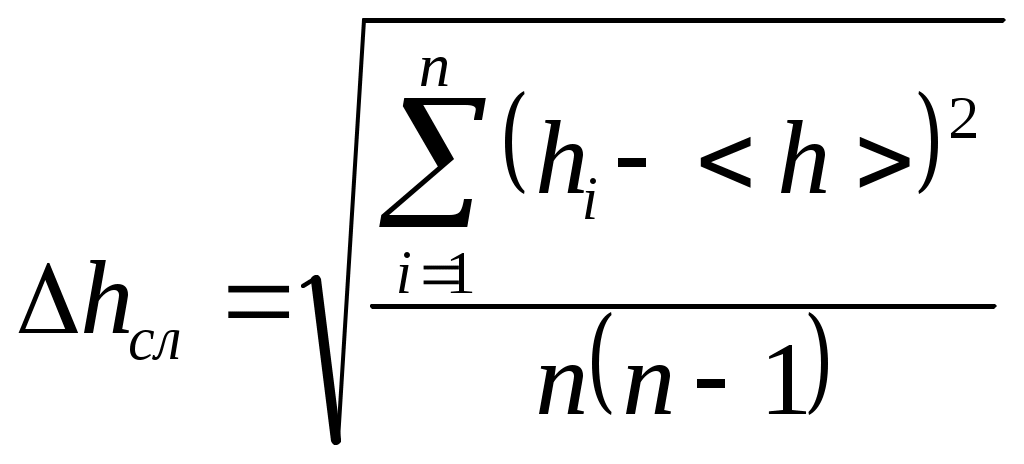  Учитывая, что 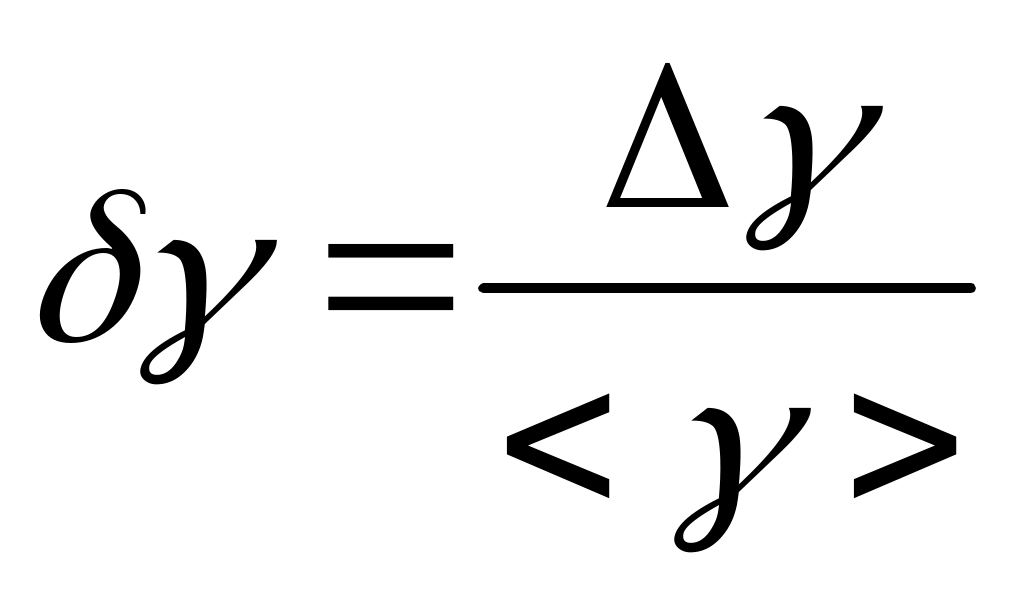 , определить абсолютную погрешность  .Записать окончательный результат в стандартной форме.  Таблица 2
Контрольные вопросы Что называется теплоемкостью тела, молярной и удельной теплоемкостью? Какова связь между ними? ___________________________________________________________________________________________________________________________________________________ Какова связь между молярными теплоемкостями при постоянном объеме и постоянном давлении? Какая из них больше и почему? ____________________________________________________________________________________________________________________________________________________ Какие термодинамические процессы имеют место в данной работе? Напишите уравнения, связывающие параметры газа при этих процессах. ___________________________________________________________________________________________________________________________________________________ Какой процесс называется адиабатическим? Как могут быть осуществлены адиабатические процессы? ___________________________________________________________________________________________________________________________________________________ Каков физический смысл показателя адиабаты? ____________________________________________________________________________________________________________________________________________________ Библиографический список Тюрин Ю.И. Физика. Ч.1. Механика и молекулярная физика. Термодинамика: Учебное пособие. – Томск: Изд-во Томского ун-та, 2002. Савельев И.В. Курс физики. Т.1. Механика, молекулярная физика. – М.: Наука, 1989. Детлаф А.А. Курс физики / А.А. Детлаф, Б.М. Яворский. – М.: Высшая школа, 2000. Трофимова Т.И. Курс физики. – М.: Высшая школа, 2000. Физический практикум / Под ред. В.И. Ивероновой. – М.: Физматгиз, 1982. Лабораторный практикум по общей физике / Л.Л. Гольдин, Ф.Ф. Игошин, С.М. Козел; Под ред. Л.Л. Гольдина. – М., 1983. Лабораторный практикум по физике / Под ред. А.С. Ахматова. – М.: Высшая школа, 1980. Яворский Б.М. Справочник по физике / Б.М. Явор-ский, А.А. Детлаф. Изд. 4. – М.: Наука, 1996. Краткий справочник для инженеров и студентов по физике / Под ред. А.Д. Полянина. – М.: Международная программа образования, 1996. Власов А.Д. Единица физических величин в науке и технике: Справочник / А.Д. Власов, Б.П. Мурин. – М.: Энергоатом, 1990. Содержание
Библиографический список 37 1) 2,39,4,37,6,35,8,33,10,31,12,29,14,27,16,25,18,23,20,21 2) 40,1,38,3,36,5,34,7,32,9,30,11,28,13,26,15,24,17,22,19 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
, 
, 
, мм
, мм
