|
ОБЩАЯ ФИЗИКА МЕХАНИКА И МОЛЕКУЛЯРНАЯ ФИЗИКА
Рабочая тетрадь
для лабораторных работ
студента группы ___________________
факультет_________________________
ФИО_________________________________
Составители: С.Х. Шигалугов, профессор, д.ф.-м.н.;
Г.В. Семенов, доцент, к.п.н;
Л.Б. Дерябина, доцент, к.т.н.;
Физический практикум предназначен для студентов всех специальностей и форм обучения, содержит теоретическую вводную часть и описание лабораторной работы.
Метрологическое введение.
Основные определения
Измерение физической величины заключается в сравнение её с однородной ей физической величиной, принятой за единицу. Различают два типа измерений физических величин: прямые и косвенные измерения.
При прямом измерении значение искомой величины сравнивают с единицей измерения непосредственно или при помощи измерительного прибора, проградуированного в соответствующих единицах.
При косвенном измерении значение искомой физической величины находят, основываясь на результатах прямых измерений других физических величин, с которыми эта искомая величина связана известной функциональной зависимостью.
Из-за действия множества искажающих факторов результат каждого отдельного измерения физической величины не совпадает с её истинным значением. Разность между результатом измерения и истинным значением измеряемой величины называют погрешностью измерений.
Различают три типа погрешностей измерений: систематические, случайные и промахи (грубые ошибки).
Систематическими называются погрешности, которые остается постоянными либо изменяются по определенному закону. К ним относятся погрешности измерительных приборов. Погрешность прибора определяется на основе паспортных данных прибора, его класса точности, точности нониуса и т. д. Классом точности средства измерения называется характеристика последнего, служащая показателем установленных для него государственным стандартом пределов погрешностей и других параметров, влияющих на точность.
Применяются следующие классы точности таких приборов: 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4.0. Обозначение класса точности прибора записывается на его шкале в виде соответствующих цифр (не заключенных в кружок). Общая формула для расчета максимальной абсолютной погрешности имеет вид
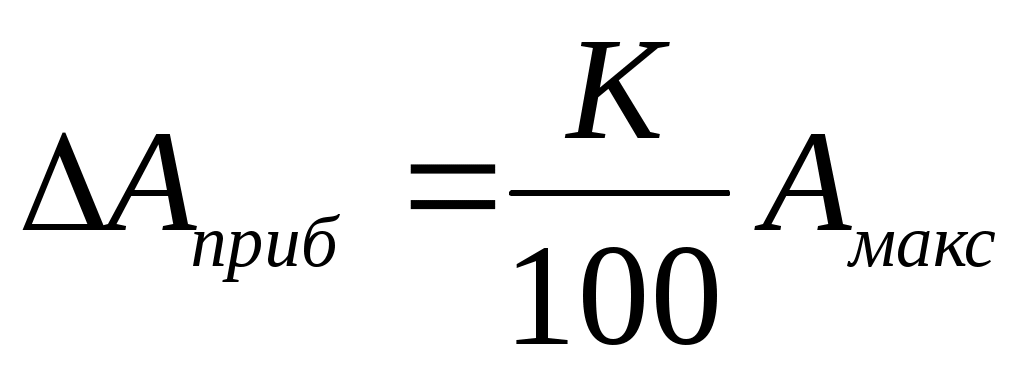 , ,
где К – класс точности прибора; Амакс – верхний предел измерений прибора (либо данного его диапазона). Например, для амперметра класса 0,5 на диапазоне Iмакс = 2 А
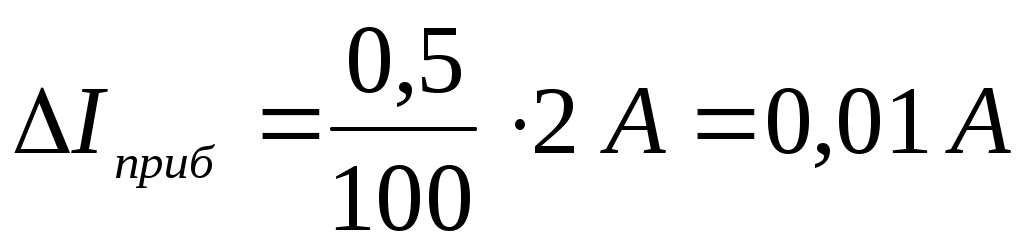 . .
Если на шкале такого обозначения нет, то данный прибор является внеклассным (невыверенным), т.е. его приведенная погрешность составляет более 4%. При этом абсолютная погрешность такого прибора принимается равной половине цены наименьшего деления шкалы.
Случайные погрешности – это ошибки, появление которых не может быть предупреждено. При многократных измерениях они подчиняются статистическим законам и их влияние на результаты измерения можно учесть.
Истинное значение xист физической величины х нельзя определить абсолютно точно. Можно лишь утверждать, что оно лежит в интервале
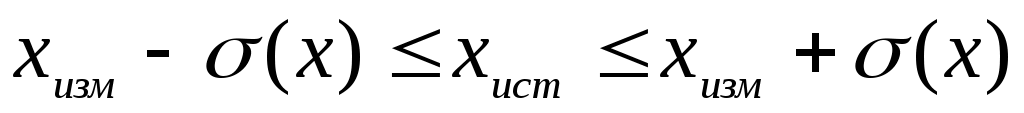 , ,
где xизм значение величины х, полученное при измерении; величина 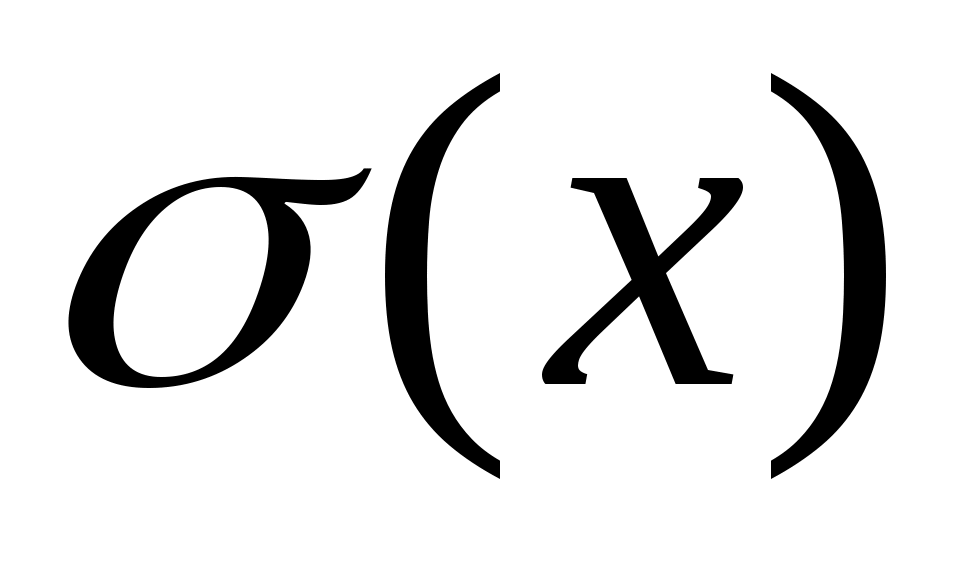 – абсолютная погрешность измерения величины х. Это неравенство принято записывать в следующем символическом виде: – абсолютная погрешность измерения величины х. Это неравенство принято записывать в следующем символическом виде:
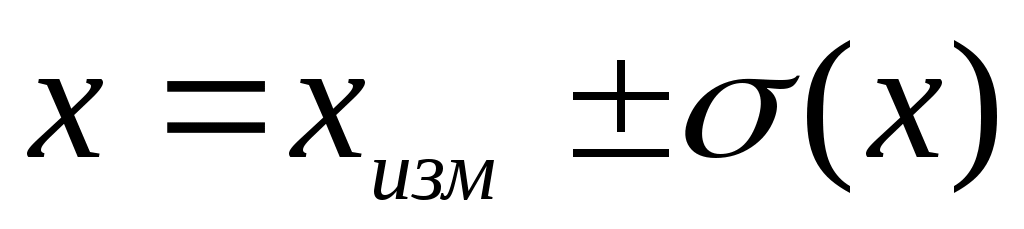 (1) (1)
За наиболее достоверное (истинное) значение непосредственно измеряемой физической величины х принимают среднее арифметическое <х> из всех n результатов ее измерений.
Промахи и грубые погрешности – это чрезмерно большие ошибки, явно искажающие результат измерения. Обычно они вызваны неправильными действиями наблюдателя, поэтому их следует отбрасывать.
Оценка погрешности результатов одного
прямого измерения
Если при повторении измерений величины х в одних и тех же условиях получается одинаковое значение x0, то проведение дальнейших измерений бессмысленно. В этом случае результат записывается в виде
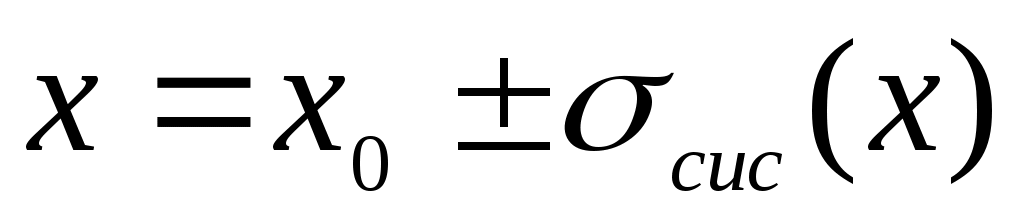 , (2) , (2)
где 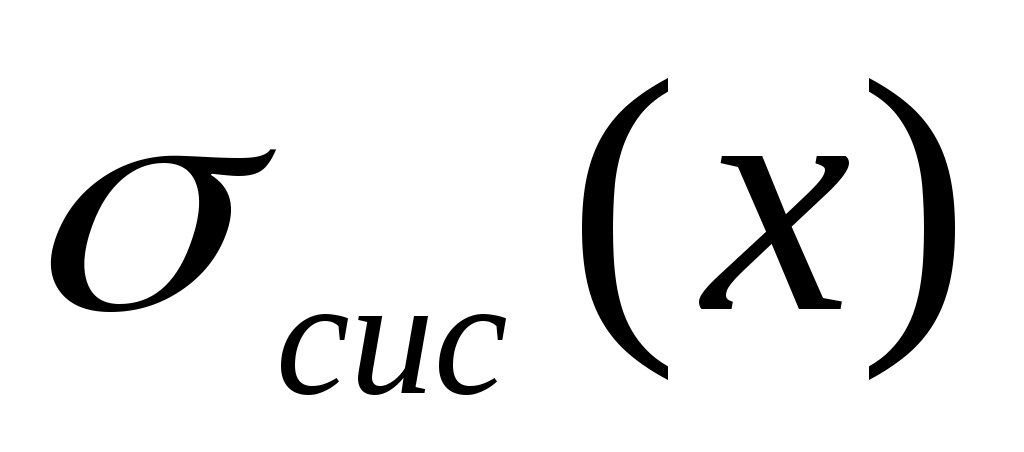 – систематическая абсолютная погрешность, связанная с точностью измерительных приборов. – систематическая абсолютная погрешность, связанная с точностью измерительных приборов.
Оценка случайной погрешности многократных
прямых измерений
Если при повторении измерений физической величины х в одинаковых условиях получают некоторые значения х1, х2, ... , xn (где п – число измерений), то результат таких измерений записывают в стандартной форме
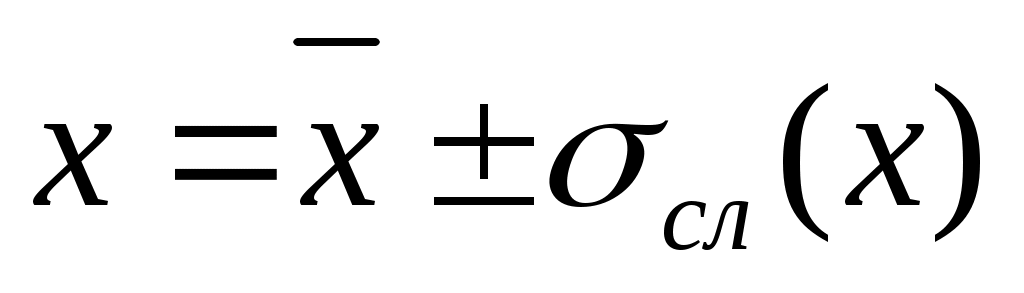 , (3) , (3)
где <х> – среднее арифметическое измеренных значений, а 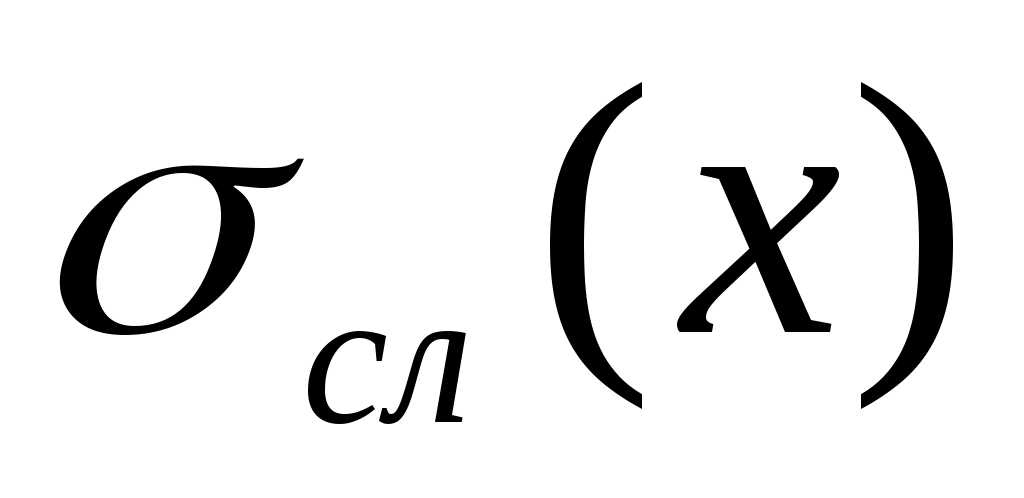 – абсолютная случайная погрешность величины х. – абсолютная случайная погрешность величины х.
Среднее значение величины х находится по формуле
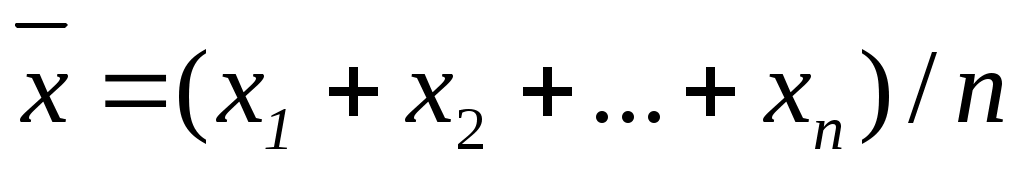 . (4) . (4)
Для нахождения случайной погрешности 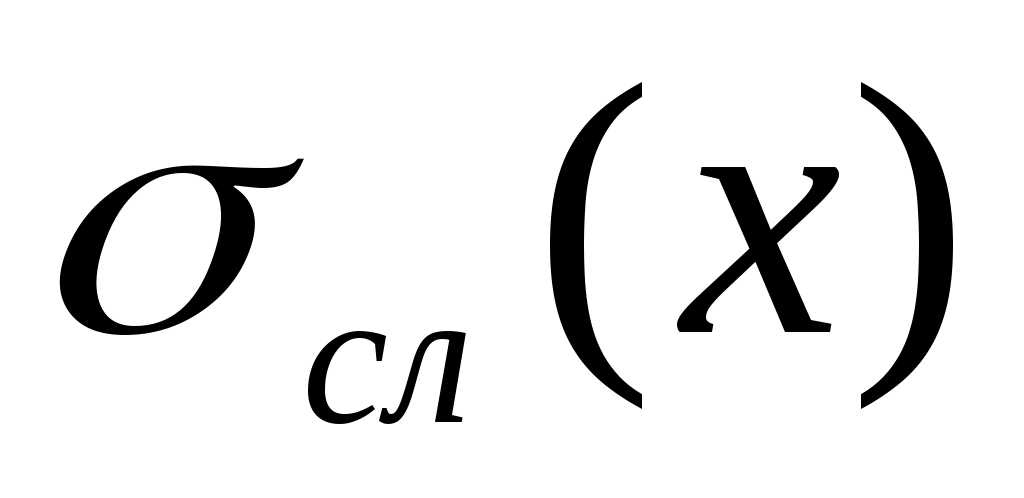 используют понятия доверительного интервала и доверительной вероятности. Доверительный интервал — это интервал используют понятия доверительного интервала и доверительной вероятности. Доверительный интервал — это интервал
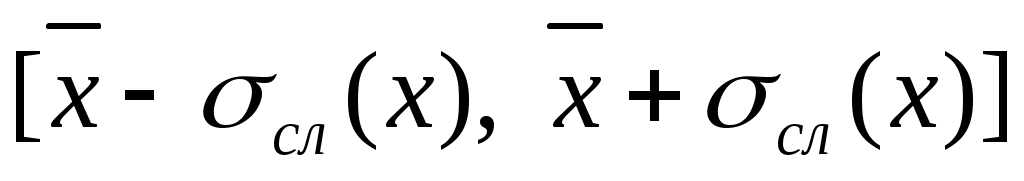 , ,
в который по определению попадает истинное значение измеряемой величины х с заданной вероятностью.
Доверительной вероятностью (надежностью) α называют вероятность того, что истинное значение измеряемой величины х попадает в заданный доверительный интервал.
В таблице (1) приведены коэффициенты Стьюдента, по которым можно определить, во сколько раз нужно увеличить стандартный доверительный интервал [± S(x)], чтобы при числе измерений п получить заданную доверительную вероятность α. За стандартный принимают интервал [± S(x)], где величина
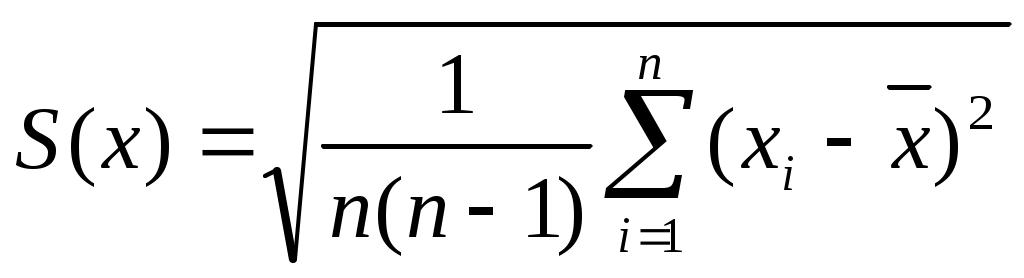 (5) (5)
называется стандартной погрешностью измерения величины х.
Коэффициенты Стьюдента t(α , п) Таблица 1
Число
измерений
|
Доверительная вероятность α
|
n
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
0,95
|
0,98
|
0,99
|
2
|
1,0
|
1,38
|
2,0
|
3,1
|
6,3
|
12,7
|
31,8
|
63,7
|
3
|
0,82
|
1,06
|
1,3
|
1,9
|
2,9
|
4,3
|
7,0
|
9,9
|
4
|
0,77
|
0,98
|
1,2
|
1,6
|
2,4
|
3,2
|
4,5
|
5,8
|
5
|
0,74
|
0,94
|
1,2
|
1,5
|
2,1
|
2,8
|
3,7
|
4,6
|
6
|
0,73
|
0,92
|
1,2
|
1,5
|
2,0
|
2,6
|
3,4
|
4,0
|
7
|
0,72
|
0,90
|
1,1
|
1,4
|
1,9
|
2,4
|
3,1
|
3,7
|
8
|
0,71
|
0,90
|
1,1
|
1,4
|
1,9
|
2,4
|
3,0
|
3,5
|
9
|
0,71
|
0,89
|
1,1
|
1,4
|
1,8
|
2,3
|
2,9
|
3,4
|
10
|
0,70
|
0,88
|
1,1
|
1,4
|
1,8
|
2,3
|
2,8
|
3,3
|
Порядок обработки результатов измерения следующий:
выполняют п измерений и записывают их результаты в таблицу;
по формуле (4) вычисляют среднее значение 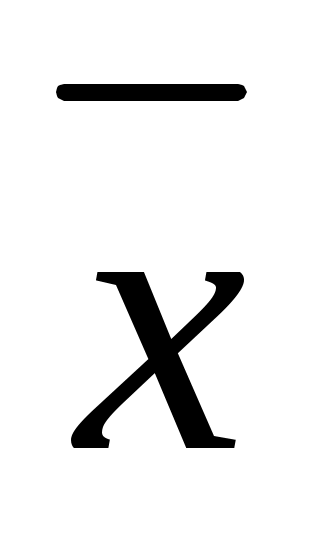 ; ;
по формуле (5) вычисляют стандартную погрешность S(x);
по таблице (3) находят коэффициент Стьюдента t(α , п) в зависимости от заданной доверительной вероятности а и числа измерений п
абсолютную случайную погрешность 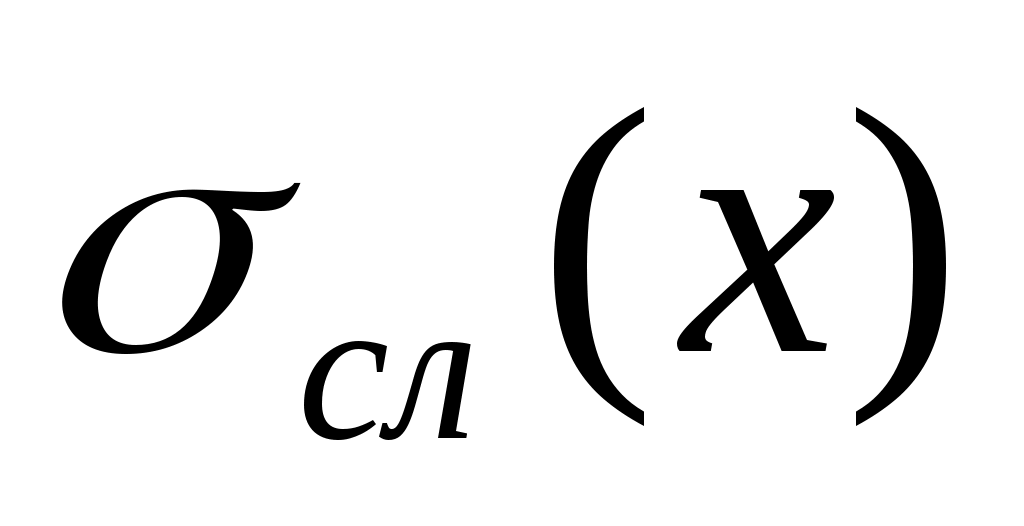 находят по формуле находят по формуле
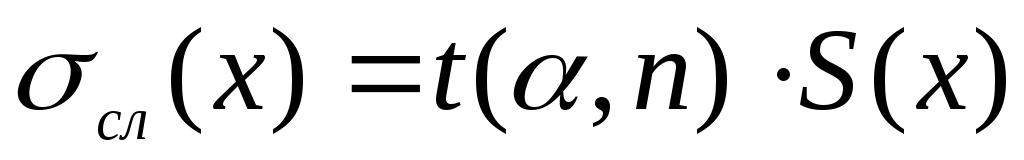 (6) (6)
Для оценки полной (суммарной) абсолютной погрешности 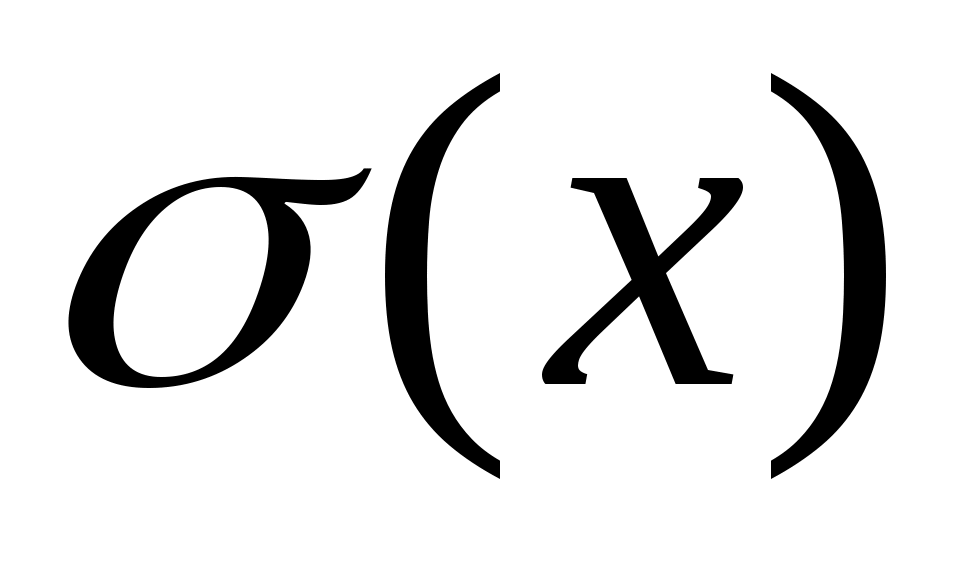 многократных прямых измерений необходимо учитывать как систематическую, так и случайную погрешности: многократных прямых измерений необходимо учитывать как систематическую, так и случайную погрешности:
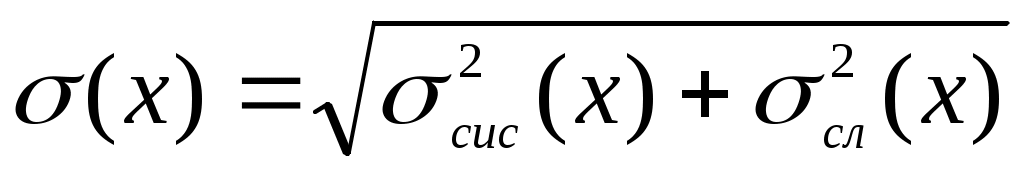 (7) (7)
Результаты измерений при этом записываются в стандартной форме
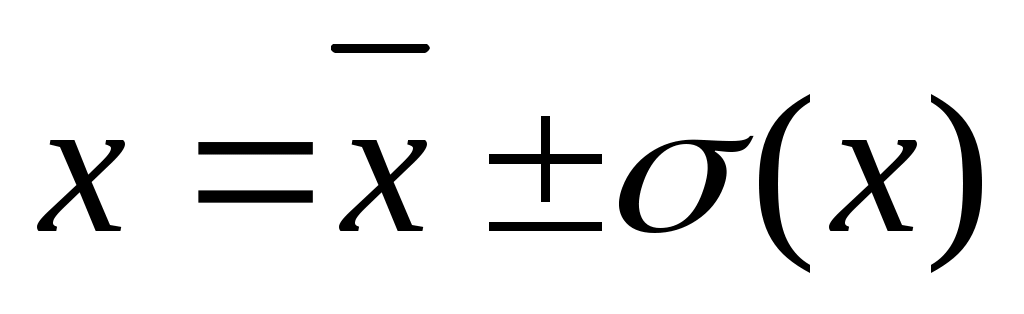 (8) (8)
Другой мерой точности результатов измерений является суммарная относительная погрешность ε(х) измерения величины х
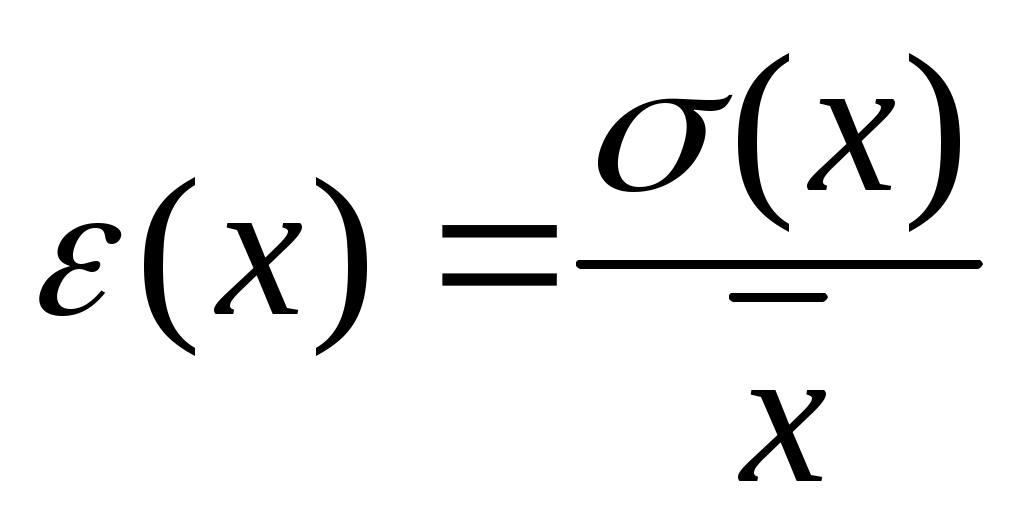 (9) (9)
Оценка случайной погрешности косвенных измерений
Пусть проводятся косвенные измерения величины А = f(x, у),где значения х и у получены прямыми измерениями. Тогда среднее значение <А> величины А вычисляется следующим образом:
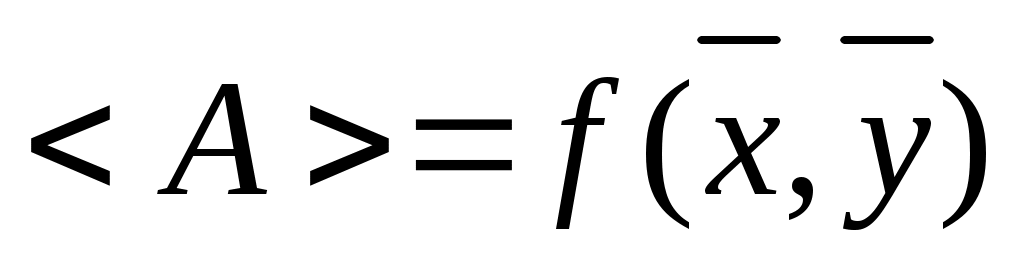 , (10) , (10)
где <х> и <у> находятся по формуле (4). Абсолютная суммарная погрешность 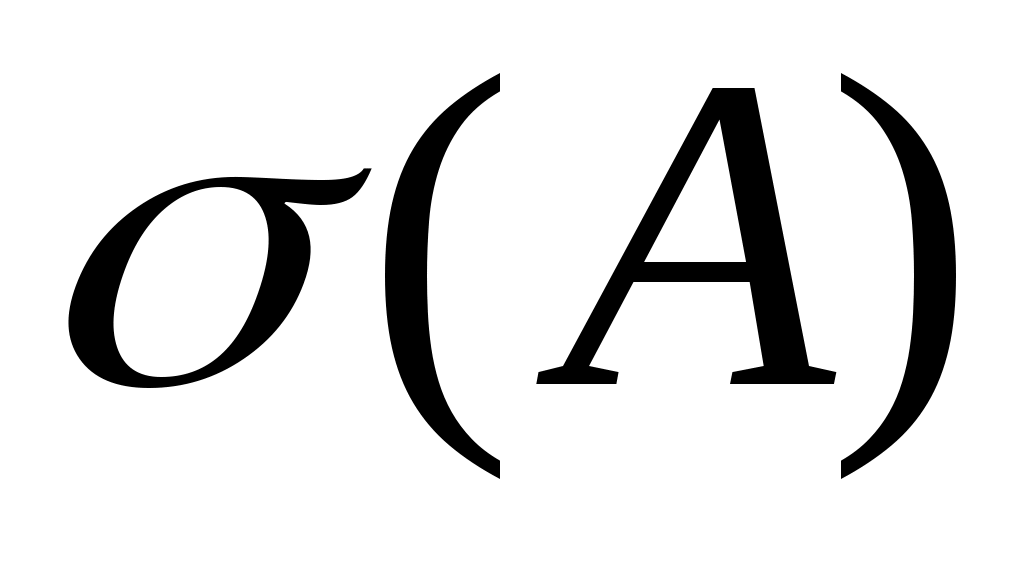 косвенного измерения величины А дается выражением косвенного измерения величины А дается выражением
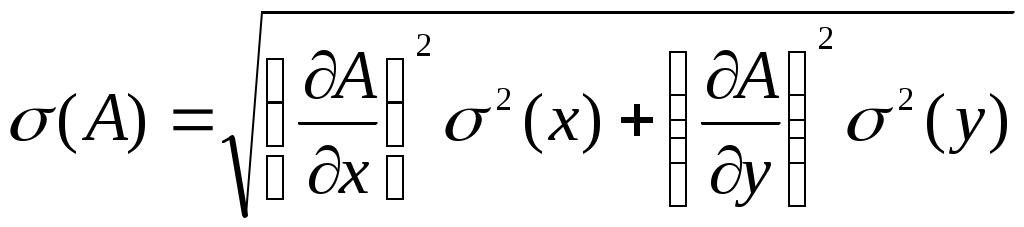 , (11) , (11)
где 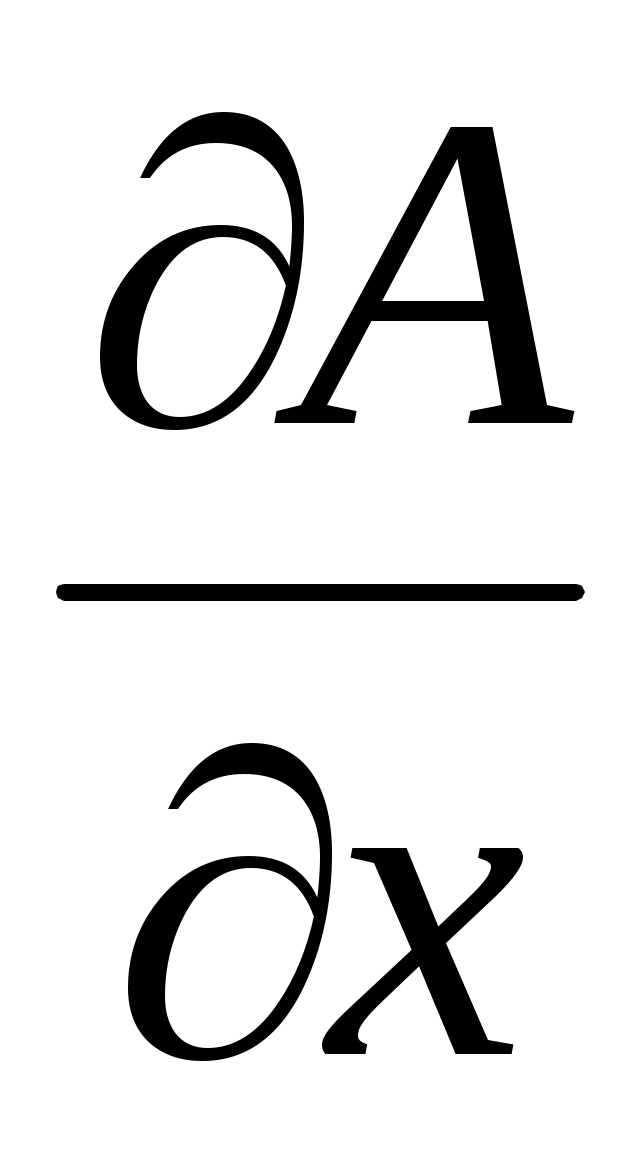 и и 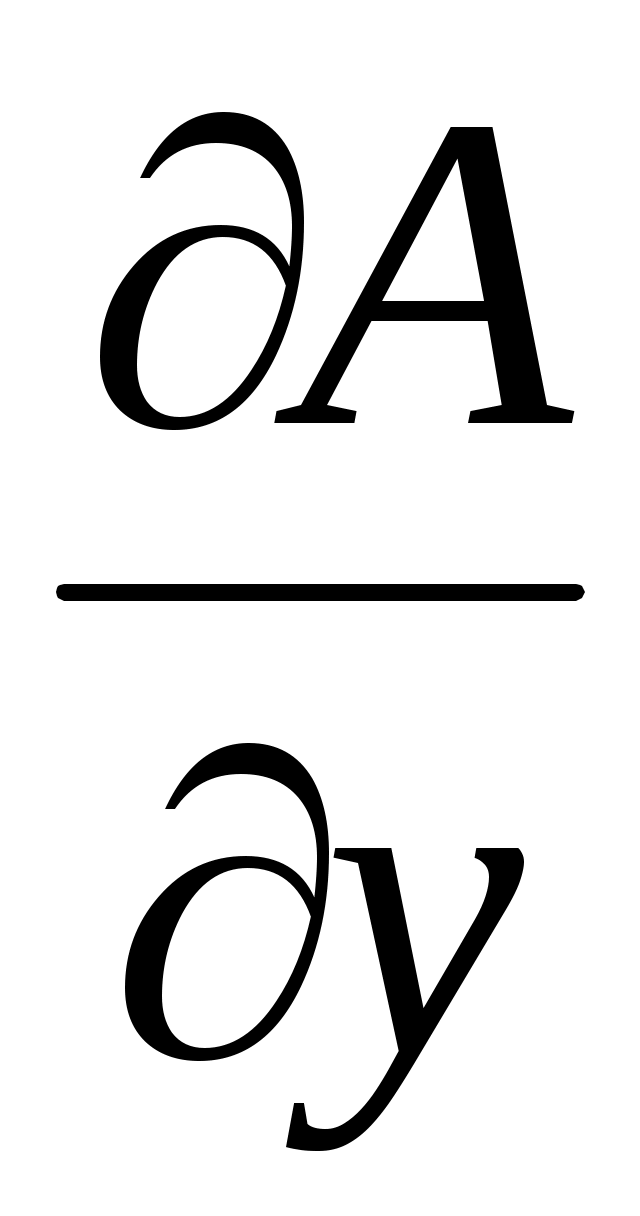 – частные производные, вычисленные, соответственно, при значениях – частные производные, вычисленные, соответственно, при значениях 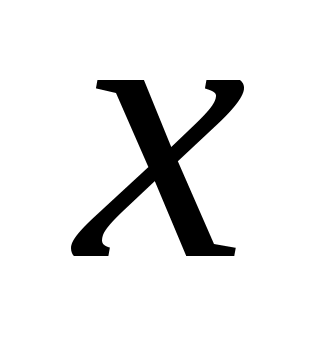 = =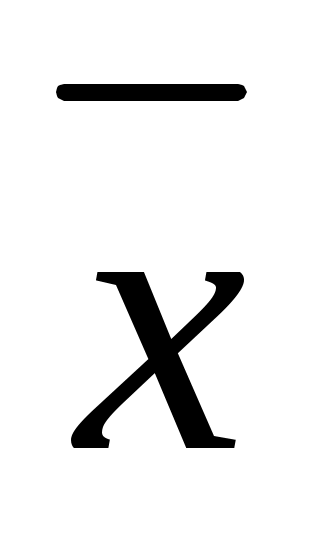 и и 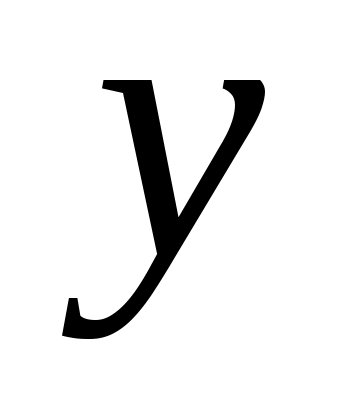 = =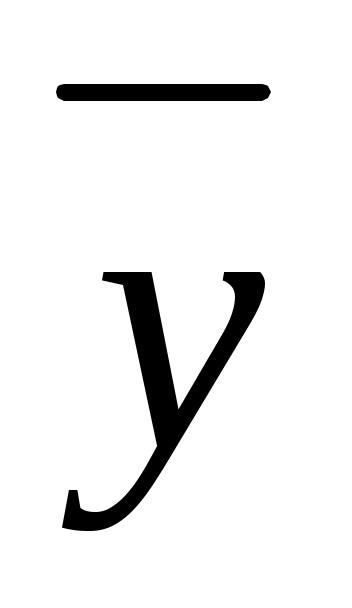 , а σ(х) и σ(у) – абсолютные суммарные погрешности прямых измерений величин х и у. , а σ(х) и σ(у) – абсолютные суммарные погрешности прямых измерений величин х и у.
В таблице 2 приведены формулы, по которым можно рассчитать абсолютные и относительные погрешности косвенных измерений для конкретных, наиболее распространенных случаев.
Таблица 2
Погрешности для простейших случаев косвенных измерений
Правила вычисления и записи погрешностей
При записи результата измерений в стандартной форме, показанной в (8), необходимо соблюдать следующие правила:
1) погрешность 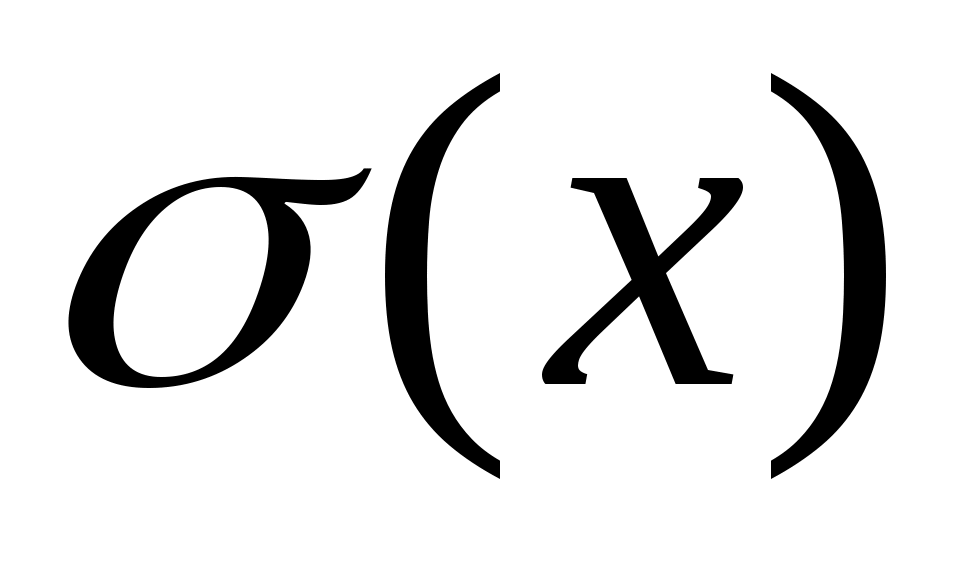 необходимо округлить до двух значащих цифр, если первая из них – единица, и до одной значащей цифры во всех остальных случаях; необходимо округлить до двух значащих цифр, если первая из них – единица, и до одной значащей цифры во всех остальных случаях;
2) при записи значения <х> необходимо указывать все цифры вплоть до последнего десятичного разряда, использованного для записи погрешности 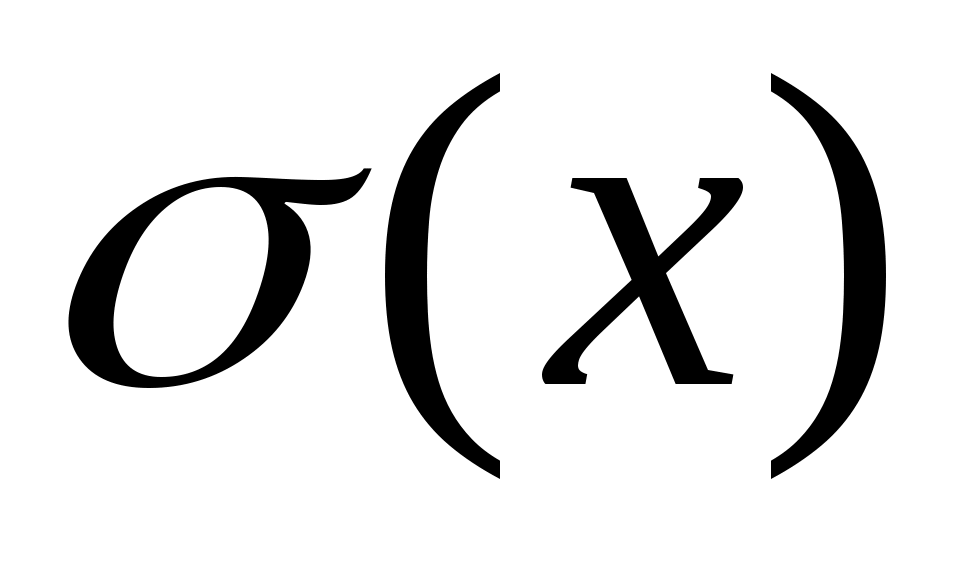 . .
Пример обработки результатов прямых измерений диаметра d шарика с помощью микрометра.
Значения di для пяти измерений приведены во втором столбце таблицы.
Номер
измерения
|
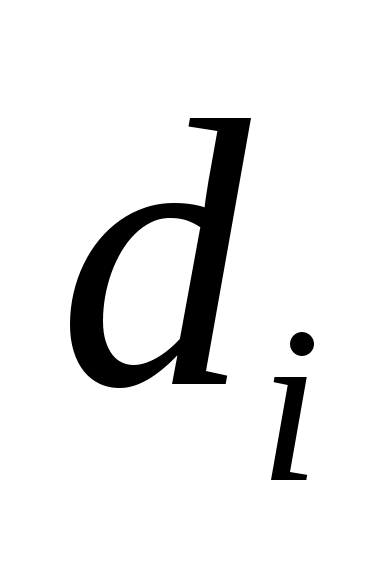 , мм , мм
|
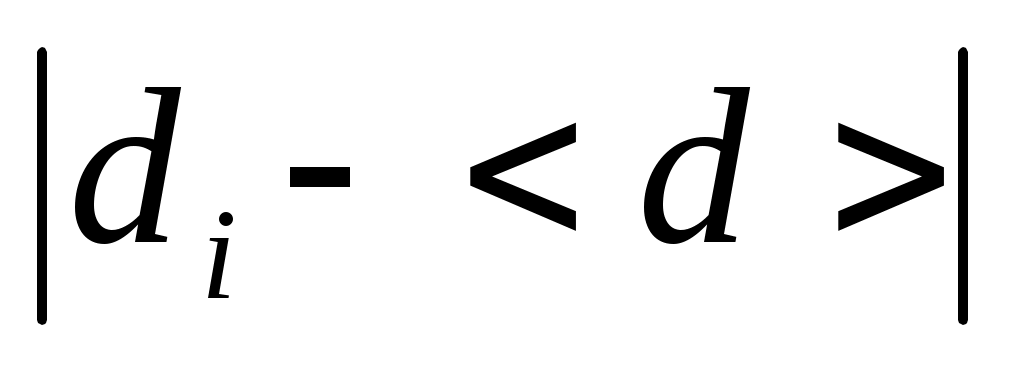 , мм , мм
|
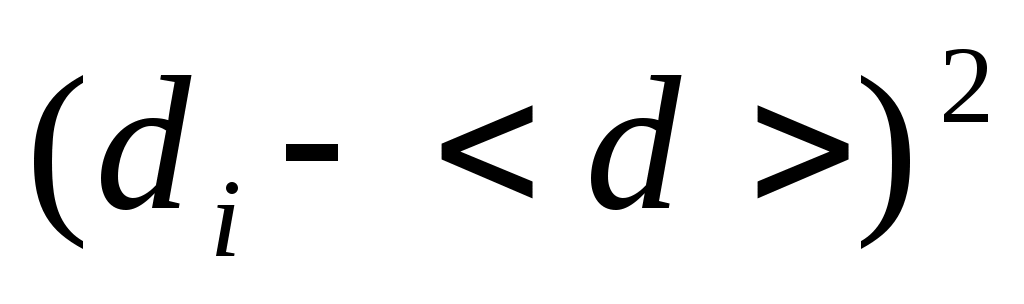 , мм2 , мм2
|
1
2
3
4
5
|
5,27
5,30
5,28
5,32
5.28
|
0,02
0,01
0,01
0,03
0,01
|
0,0004
0,0001
0,0001
0,0009
0,0001
|
Проводим расчеты:
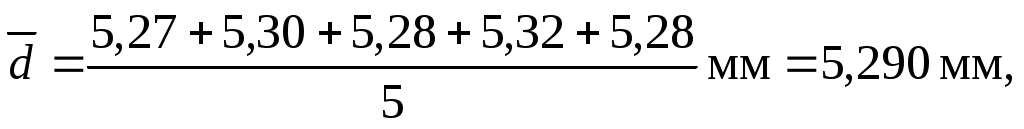 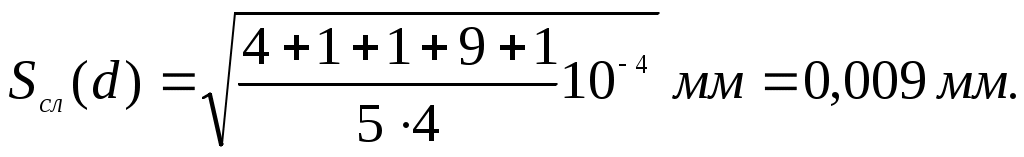
При числе измерений 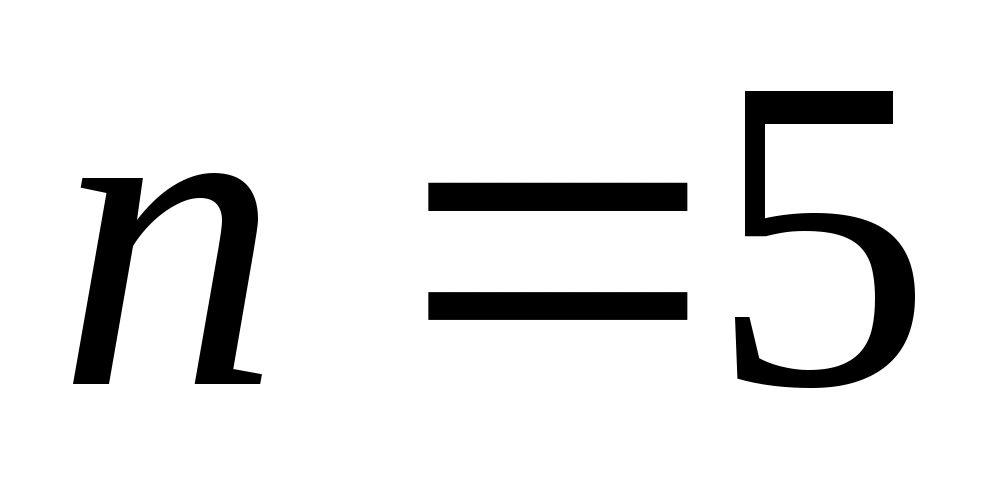 с надежностью с надежностью 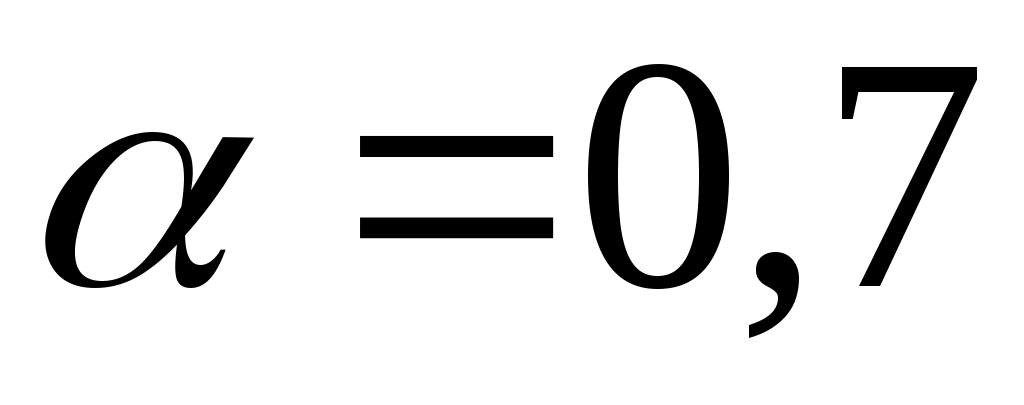 по табл. 1 находим коэффициент Стьюдента t(0,7; 5) = 1,2 и вычисляем абсолютную случайную погрешность по табл. 1 находим коэффициент Стьюдента t(0,7; 5) = 1,2 и вычисляем абсолютную случайную погрешность
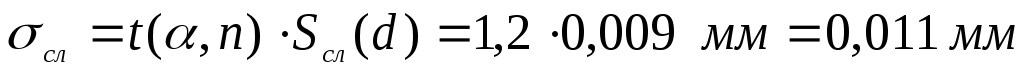
Полагая систематическую погрешность микрометра равной его точности (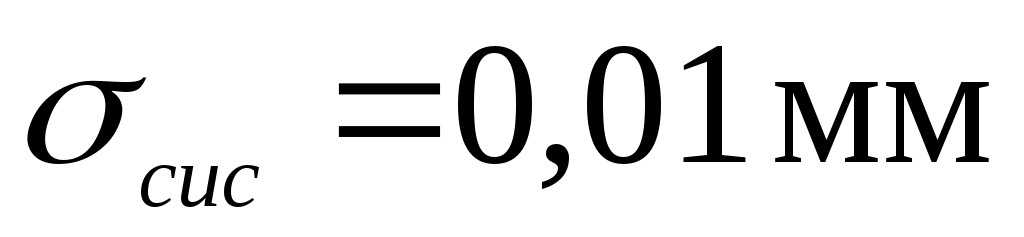 ), найдем полную абсолютную погрешность диаметра шарика: ), найдем полную абсолютную погрешность диаметра шарика:
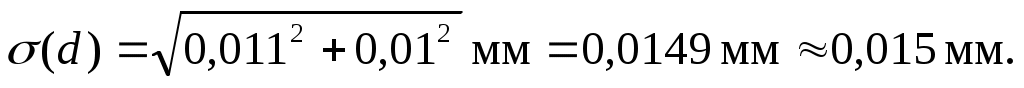
Правильная запись результата измерений:
d= (5,290 ± 0,015) мм.
Примеры неправильной записи результата измерений:
1) d= (5,29 ± 0,01) мм – погрешность занижена больше чем на 15 — 20% из-за нарушения правила 1;
2) d= (5,29 ± 0,015) мм – нарушено правило 2;
3) d= (5,2900 ± 0,0149) мм – не выполнено правило 1.
|
 Скачать 1.27 Mb.
Скачать 1.27 Mb.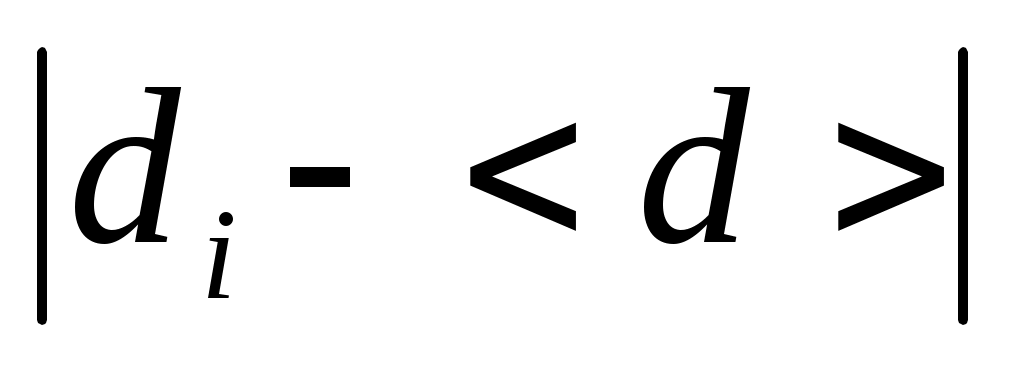 , мм
, мм