Р.Т. Часть 1. Механика и молекулярная физика. Общая физика механика и

• Название: Общая физика механика и
• Дата: 05.01.2023
• Размер: 1.27 Mb.
• Имя файла: Р.Т. Часть 1. Механика и молекулярная физика.doc
• Тип: Документы; #873454
• страница: 3 из 4

T²_П, с


l, м

Графически
Лабораторная работа 1.1

Изучение законов поступательного движения

с помощью машины Атвуда

Допуск____________________________________________________

Отработка_______________________________________________

Защита___________________________________________________

Цель работы: экспериментальная проверка кинематических законов

равномерного и равноускоренного движения и второго закона Ньютона.
Краткое теоретическое введение

Х арактеристики поступательного движения любого тела могут быть определены с помощью кинематических соотношений на основе прямых измерений расстояния (пути), проходимого телом, и времени, потребовавшегося для этого. Убедиться в этом можно с помощью лабораторной установки "машина Атвуда".

На рис.1 представлена кинематическая схема установки. К концам невесомой и нерастяжимой нити, перекинутой через невесомый блок, подвешены два одинаковых груза массой М каждый. На правый груз положен небольшой перегрузок массой m, в результате чего система грузов получает ускорение . При прохождений правым грузом кольца К перегрузок m отцепляется, и система грузов продолжает движение уже по инерции, т.е. с нулевым ускорением. Скорость этого равномерного движения (в предположении равенства нулю сил трения и сопротивления воздуха) равна конечной скорости движения системы грузов на участке равноускоренного движения (участок h на рис.1) и определяется кинематическим соотношением

(l)

Величину скорости υ нетрудно определить косвенным образом по прямым измерениям пути Н и времени t прохождения этого пути на участке равномерного движения (с отцепленным перегрузом)

(2)

Сопоставляя (l) и (2), получаем экспериментальное значение ускорения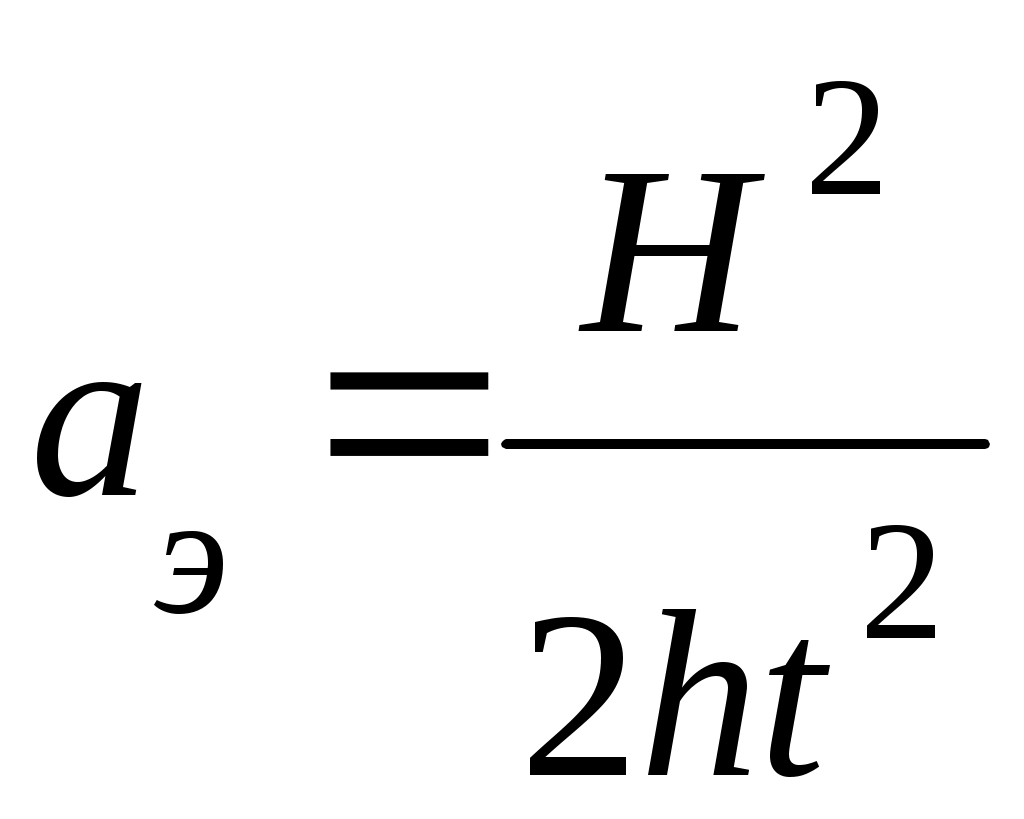

(3)

определяемое косвенный образом по прямым измерениям путей Н, h и времени t.

С другой стороны, согласно второму закону Ньютона (также при указанных выше допущениях: равенства масс М основных грузов, невесомости и нерастяжимости нити, невесомости блока и равенства нулю сил трения и сопротивления воздуха) расчетное ускорение системы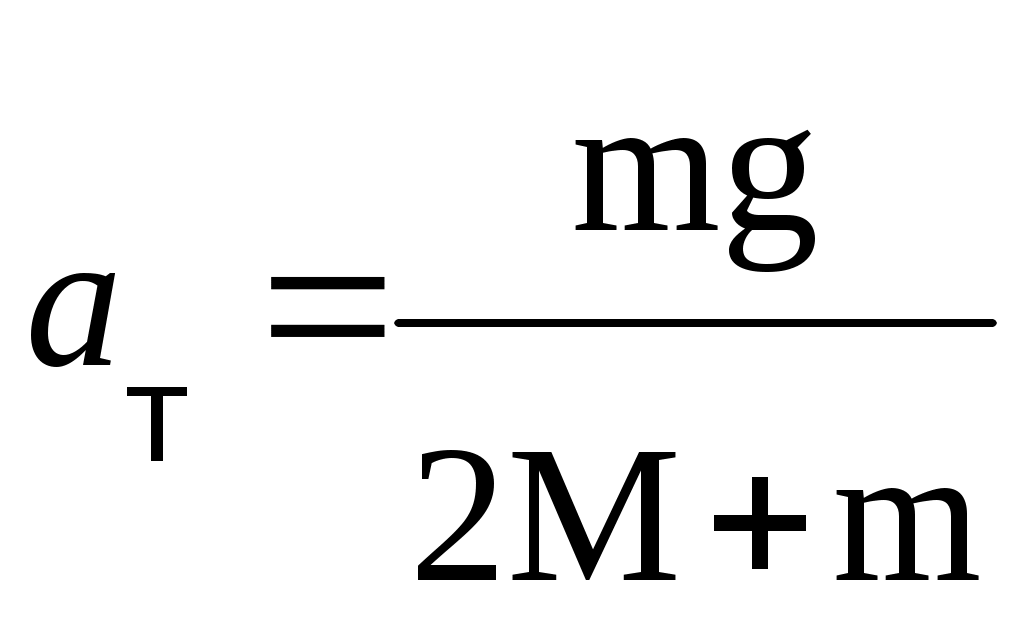

(4)

что позволяет определить величину a_т косвенным образом по прямым измерениям масс М и m и табличному значению ускорения свободного падения g.

Экспериментальная установка. Методика эксперимента

Общий вид установки Атвуда представлен на рис.2.

На вертикальной колонне I, установленной на основании 2, находятся три кронштейна - нижний 3 (неподвижны), средний 4 и верхний 5 (неподвижные), а также верхняя втулка 6. Верхний 5 и средний 4 кронштейны можно перемещать вдоль колонны 2 и Фиксировать в любом положении, меняя таким образом длины участков равномерного и ускоренного движения (h, H на рис.1). Все кронштейны снабжены указателями положения, облегчающими отсчет пути по укрепленной на колонне I миллиметровой шкале 15. Основание 2 оснащено регулируемыми по высоте ножками 7, позволяющими выравнивать положение установки. На верхней втулке 6 при помощи верхнего диска 8 закреплены: узел подшипника 9, легкий блок 10 (вращающийся в подшипнике 9) и электромагнит 11. Через блок 10 перекинута нить 12 с привязанными на ее концах грузами 14 и 16 (см. также рис.1). При подаче на установку электропитания электромагнит II при помощи фрикционной муфты удерживает систему блок-нить-грузы в состоянии покоя (груз 14 с перегрузком 13 в верхнем положении).

На среднем кронштейне 4 укреплен "фотоэлектрический датчик 17, включающий электронный миллисекундомер 20 при прохождении сквозь отверстие в кронштейне 4 груза 14 (при этом перегрузок 13 отцепляется и остается на кронштейне 4). На нижнем кронштейне 3 укреплен еще один фотоэлектрический датчик 19, выключающий электронный миллисекундомер 20 при достижении грузом 14 основания 18 нижнего кронштейна 3.

Установка снабжена комплектом из трех перегрузков 13, массы которых m₁, m₂ и m₃ измеряются прямым взвешиванием на аналитических весах (как и массы М грузов 14 и 16); значения M, m₁, m₂ и m₃ могут быть указаны преподавателем или лаборантом (без взвешивания).




Методика проведения эксперимента

1. 
   Подключите установку к сети 220 В. Опустите левый груз 16 вниз до упора, нажмите последовательно кнопки "сеть" и "сброс" на лицевой панели электронного секундомера 20 (установка включена, электромагнит 11 удерживает блок 10 в состоянии покоя, табло электронного секундомера показывает нулевой отсчет). Положите на правый груз 14 один из перегрузков 13 (масса m₁)
   
2. 
   Установите средний кронштейн 4 на высоту Н₁(cм. рис. 1); при необходимости переместите верхний кронштейн 5 в положение, обеспечивающее отсчет начала пути правого груза 14 с перегрузком 13 массой m₁, находящихся в верхнем положении.
   
3. 
   Нажав кнопку «пуск», предоставьте системе «грузы-нить-блок» возможность придти в движение и поавтоматически включающемуся электронному секундомеру 20 определите время t прохождения правым грузом 14 (без перегруза m₁ остающегося на среднем кронштейне 4) расстояния Н₁. Полученное значение t вместе со значениями Н₁, h₁ и m₁ занесите в соответствующие графы табл. 1
   
4. 
   Приведите установку в исходное состояние, для чего отключите установку (кнопка «сеть»), вновь опустите левый груз 16 вниз до упора (правый груз 14 с вновь установленным на нем же перегрузком массы m₁ опять займет верхнее положение), нажмите последовательно кнопки «сеть» и «сброс»
   

5. 
   Дважды повторите измерения по пунктам 3-4 (т.е. с неизменными расстояниями Н₁, h₁ и массой перегрузка m₁) и полученные значения и t также заносите в табл.1.
   
6. 
   Проведите две серии трехкратных измерений промежутка времени t для двух других перегрузков (массы m₂ и m₃) при сохранении постоянными расстояний Н₁ и h₁. Полученные значения t_1,2,3 для перегрузка m₂ и t_1,2,3 для перегрузка m₃ также занесите в табл.1.
   

7. 
   Пользуясь указаниями преподавателя и руководствуясь пунктами 3-6, проведите ещё два блока измерений t_1,2,3 по три серии трехкратных измерений в каждом для Н₁ и другой высоты h₂< h₁.
   

Измерения. Обработка результатов измерений

1. 
   Используя результаты прямых измерений масс, расстояний и средних значений интервалов времени (см. табл.1), а также справочное значение ускорения свободного падения (g=9.81 м/с²), вычислите экспериментальные a_э и расчетные a_т значения ускорений с использованием кинематической и динамической формул.
   

Написать расчетные формулы:

Кинематическая



________________________________________________________________________

Динамическая

________________________________________________________________________


Полученные значения внести в табл.1.

Таблица 1

H и h, м m, кг	t, с	Δt , с	aэ,м/с2	aт ,м/с2
Н1 = m1 = h1 = m2 = m3 =	1
	2
	3
среднее значение
Н2 = Н1 m1 = h 2 = m2 = m3 =

2. 
   Постройте графики зависимости , сравните средние значения экспериментальных и расчетных величин ускорения, полученных для разных масс и одной высоты.
   

График зависимости



Вывод по работе:

3. 
   На основе формулы (3) определите по известным правилам относительные погрешности значений ускорений, учитывая, что при прямых измерениях допущены следующие абсолютные погрешности: = 10^-3 м, = 10^-3 м, = 10^-6 кг, = 10^-6 кг, - из табл. 1 , = 510^-3 м/с².
   

Контрольные вопросы

1. 
   В чем состоит цель лабораторной работы? Какие законы проверяются в данной работе?
   

______________________________________________________________________________________________________________________________________________

2. 
   Что называется ускорением?
   

______________________________________________________________________________________________________________________________________________

3. 
   Определите ускорение движения, заданного законом
   

_______________________________________________________________________

_______________________________________________________________________

4. 
   Сформулировать три закона Ньютона.
   

_______________________________________________________________________

_______________________________________________________________________

5. 
   Записать уравнение второго закона Ньютона для системы, в которой сила трения в блоке равна и блок имеет момент инерции J.
   

______________________________________________________________________________________________________________________________________________

6. 
   Написать закон скорости равноускоренного (равнозамедленного) движения.
   

____________________________________________________________________________________________________________________________________________________

7. 
   Начертить график зависимости пути от времени равноускоренного (равнозамедленного) движения.
   

8. 
   Произведите вывод формул (3) и (4) в данной работе и объясните физический смысл входящих в них величин.
   

____________________________________________________________________________________________________________________________________________________

____________________________________________________________________________________________________________________________________________________

9. 
   Постройте (качественно) графики зависимостей S(t), υ(t), а(t) на участках равноускоренного и равномерного движения правого груза с перегрузком и без него.
   

Лабораторная работа I.5

Изучение вращательного и поступательного движения твердого тела на примере маятника Максвелла
Допуск____________________________________________________

Отработка_______________________________________________

Защита___________________________________________________
Цель работы: изучение законов плоскопараллельного движения тел; экспериментальное определение моментов инерции тел с помощью маятника Максвелла

Краткое теоретическое введение

Н
а валик радиуса r (рис.1) наглухо насажен маховик – диск радиуса R. К валику симметрично относительно диска прикреплены две нити одинаковой длины, с помощью которых маятник подвешивается к верхнему кронштейну. Нити симметрично и в один ряд наматываются на валик, и валик поднимается. При свободном опускании валика с диском нити разматываются до полной длины в нижнем положении маятника, а затем, поскольку диск продолжает вращаться по инерции в том же направлении, вновь наматываются на валик. Дойдя до верхнего положения, диск вновь начинает спускаться вниз и т.д. Маятник таким образом совершает плоское движение – все его точки перемещаются в плоскостях, перпендикулярных оси валика.

Для описания движения маятника используются два уравнения динамики твердого тела:

уравнение движения центра масс С (второй закон Ньютона)
(1)

уравнение вращения вокруг оси, проходящей через центр масс в пренебрежении моментом сопротивления, записывается в виде:
(2)

где m – масса тела, a_с – линейное ускорение центра масс, Т – сила реакции нити, J_c – момент инерции тела относительно оси, проходящей через центр масс,  - угловое ускорение тела, r – радиус валика.

Если нить наматывается и разматывается по валику без проскальзывания, то из кинематического соотношения:

(3)

(4)

где t – время движения маятника, h – проходимое при этом расстояние.
Решая (1) – (4) совместно относительно J_с, получим расчетную формулу для экспериментального определения момента инерции маятника:
(5)

Здесь, в соответствии с конструкцией маятника, его масса является суммой масс трех тел: валика, диска и сменного кольца, т.е. .

Полученное экспериментально, т.е. вычисленное по формуле (5) значение момента инерции теперь необходимо сопоставить с теоретическим моментом инерции маятника, который можно вычислить по геометрическим размерам и массам деталей маятника.

Момент инерции маятника, естественно, равен сумме моментов инерции трех тел: валика, диска и сменного кольца:

(6)
Соотношение (6) можно записать:

(7)

где m_в – масса валика, m_д – масса диска, m_к – масса сменного кольца, r – радиус валика, R - внешний радиус диска, R_к – внешний радиус сменного кольца.