Общая характеристика растворов. Межмолекулярные взаимодействия вандерваальсовские и специфические. Уравнение ЛеннардДжонса Здравствуйте. Меня зовут Юрий Федорович Опруненко
 Скачать 1.21 Mb. Скачать 1.21 Mb.
|
|
pг = kгNг где кг – коэффициент пропорциональности или константа Генри, Nг – мольная доля растворенного газа. Константа Генри обычно измеряется в паскалях Па. Обратим внимание, что константа Генри постоянна при данной температуре, а при изменении температуры ее значение изменяется. Ее величины для разных систем приводятся в справочниках по термодинамическим свойствам веществ. В общем случае, константа Генри зависит от природы газа, природы растворителя и температуры. Таблица. Константы Генри для воды при 298 K для некоторых газов. Газ H2 He Ar N2 O2 CO кг 1311 2649 662 1610 773 29,3 Закон Генри играет очень важную роль в промышленности. Так при получении водорода с помощью процесса Боша (разд. 12.1) для удаления диоксида углерода из водорода газообразную смесь пропускают под давлением 50 атм через воду. СО2 хорошо растворяется в воде и практически полностью удаляется от водорода. Из уравнения (6.1) следует, величина что кг определяется выбором единиц давления и концентрации. pг/kг = Nг Две формулировки закона Генри: Парциальное давление газа над поверхностью его раствора прямо пропорционально мольной доле растворенного газа Мольная доля растворенного газа пропорциональна парциальному давлению газа над раствором Закон Генри справедлив для сильно разбавленныъ растворов газов, близких к идеальным. Так при растворении даже таких плохо растворимых в воде газов, как аргон, закон Генри остается справедлив для давлений до 5 атм, т.е. когда аргона в растворе относительно мало. Для умеренно растворимых газов, таких как кислород или водород, постоянное значение константы Генри наблюдается лишь при повышенных температурах, опять же когда концентрация газа в растворе невелика. В области высоких давлений и сравнительно больших концентраций закон Генри модифицируется следующим образом: fг/kг = Nг fг = fpг fг – фугитивность (или летучесть) газа, f - безразмерный коэффициент фугитивности, зависящий от р и Т. Закон Генри является частным случаем общего закона Дальтона. Если речь идет о растворении не одного газообразного компонента, а смеси газов, то растворимость подчиняется закону Дальтона: Растворимость каждого из компонентов газовой смеси при постоянной температуре пропорционально парциальному давлению компонента над жидкостью и не зависит от общего давления смеси и природы (индивидуальности) других компонентов Парциальное давление компонента расчитывается по формуле: pi = pобщ x(Xi) pi = парциальное давление компонента Xi, pобщ – общее давление газовой смеси, x(Xi) – молярная доля i-го компонента. Растворимость газов снижается в присутствии электролитов. Снижение растворимости газов в растворах электролитов объясняется процессом сольватации. Молекулы растворителя прочнее связываются с ионами электролитов, чем с молекулами газов, значительная часть молекул растворителя используется для сольватации ионов и выключается из участия в растворении газов (число молекул незадействованных молекул растворителя становится меньше и его растворяющая способность падает). Это явление называется высаливанием. (например, что происходит при подсаливании пива?). Закон, выражающий эту зависимость в количественном виде, называется законом И.М. Сеченова (1892 г.). В экспоненциальной форме закон выглядит следующим образом: 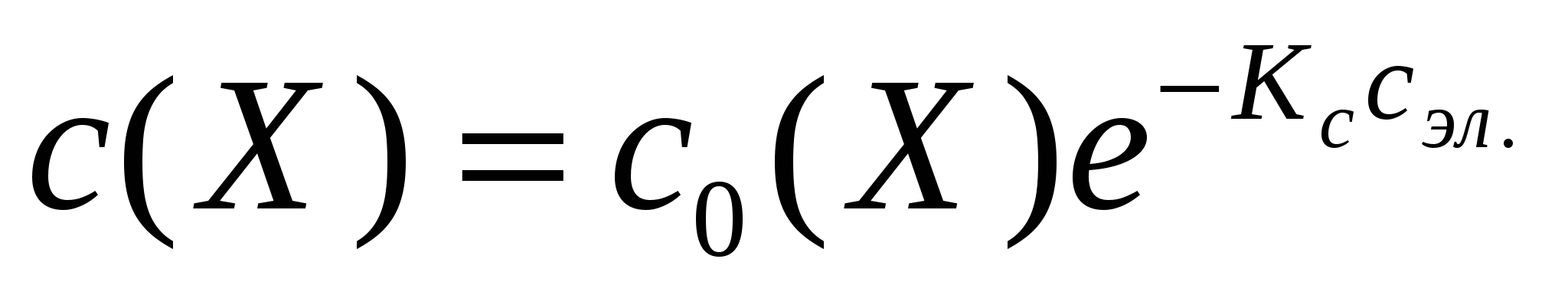 С(Х) растворимость газа Х в присутствии электролита, со(Х) растворимость газа Х в чистом растворителе, сэл – концентрация электролита – все концентрации должны быть выражены в одних единицах, Кс – константа Сеченова, являющаяся эмпирическим коэффициентом и зависящая от природы газа, природы электролита и температуры. В логарифмическом виде закон Сеченова выглядит так: ln(co(X)/c(X)) = Кccэл Отношение co(X)/c(X) показывает во сколько раз снизилась растворимость газа в растворе электролита относительно его растворимости в воде. Для удаления газов из жидкостей кроме высаливания используется также кипячение, барботирование инертных газов, а также многократные операции замораживание-откачка-размораживание-установление равновесия-замораживание-отккачка. Биологическое значение законов Генри-Дальтона и Сеченова Законы Генри-Дальтона и Сеченова имеют большое значение в биологии и медицине. Например, кессонная болезнь является проявлением закона Генри. На глубине в 40 м общее давление повышается примерно 4 раза и составляет 400 кПа. Растворимость азота в плазме крови в соответствии с законом Генри в 4 раза больше чем на поверхности моря. Если подымать водолаза из глубины слишком быстро, то часть газов (в основном азота) выделяется в виде пузырьков, закупоривают мелкие сосуды в различных органах и тканях (эмболия), что может привести к смерти. Во избежания кессонной болезни водолазам приходится медленно возвращаться на поверхность или пользоваться вместо воздуха смесью из 80% гелия и 20% кислорода. Гелий не вызывает кессонной болезни, поскольку его растворимость в крови (воде) гораздо меньше, чем у азота. Проявлением закона Генри и моделью для понимания процессов эмболии является выделение углекислого газа при открывании бутылки шампанского. ВОДЯНОЙ ГАЗ (процесс Боша). Получают при восстановлении водяного пара раскаленным коксом (углеродом) в специальных аппаратах — газогенераторах: С+Н2О(г)= СО+Н2. ↑ Образующаяся при этом смесь оксида углерода (II) и водорода называется водяным газом. Он широко используется как горючий газ, в качестве сырья для синтеза различных химических продуктов (аммиака, метанола и др.). При обработке водяного газа водяным паром в присутствии железного катализатора монооксид углерода превращается в диоксид, который легко растворяется в воде при повышенном давлении (50 атм) или в растворах щелочей: СО(г)+Н2О(г) = СО2(г)+Н2(г). ↑ Затем СО2 удаляют, пропуская реакционную смесь через воду при давлении 50 атм или горячий раствор карбоната калия. Лекция 9 Растворы жидкостей в жидкостях. Типы растворов и их связь с величиной ММВ молекул, образующих раствор. Построение диаграмм давление(температура) – состав. Свойства совершенных растворов. Давление пара и температура кипения для жидких растворов. Законы Гиббса-Коновалова. Азеотропы. Термодинамическое обоснования законов Гиббса-Коновалова. Законы Вревского Растворы жидкостей в жидкостях довольно часто встречаются и очень важны для промышленности. На использовании таких растворов во многом базируется нефтяная (получение всевозможных бензинов, керосинов, лигроинов), винокуренная и фармацевтическая промышленность. Существует три разновидности двухкомпонентных жидких смесей, т.е. растворов жидкостей в жидкостях:
Таким образом растворимость жидкостей в жидкостях зависит от природы растворителя и растворяемого вещества, температуры, присутствия в растворе посторонних веществ и т.д. 1-й класс. Жидкости, нерастворимые друг в друге. 1-й класс составляют смеси жидкостей, молекулы которых очень значительно различаются по полярности, как например, вода и н-октан. Эти две жидкости образуют два слоя: верхний - углеводород, нижний -вода. В качестве примера нерастворимых друг в друге жидкостей (бензол и вода, нефть и вода, эфир и вода и т.д.) С физической точки зрения в жидкостях такого класса силы ММВ между однородными молекулами не равны нулю, а между разнородным равны нулю. FA-A 0, FB-B 0, FA-B = 0 2-й класс составляют смеси, ограниченно растворимые друг в друге (анилин-вода, фенол-вода). Жидкости этого класса характеризуются тем, что ММВ между однородными молекулами гораздо выше, чем между разнородными, т.е. FA-A FA-B, FB-B FA-B, FA-B 0 3-й класс составляют смеси жидкостей, в которых компоненты неограниченно растворимы друг в друге. Жидкости 3-го класса подразделяются на 3 подкласса. 1-й подкласс. Жидкости, растворимые друг в друге и не имеющие постоянной температуры кипения. Их подразделяют еще на на смеси с идеальными и реже неидеальными (реальными) свойствами. Идеальные растворы характеризуются еще тем, что силы ММВ между однороднымии разнородными молекулами равны. FA-A = FB-B = FA-B Реальные растворы могут проявлять положительные отклонения от свойств идеальных растворов, для которых FA-A FA-B, FB-B FA-B Т.е. в таких растворах происходит диссоциация ассоциатов, образованных из однородных молекул. Реальные растворы могут проявлять отрицательные отклонения от свойств идеальных растворов вследствие преобладания процессов ассоциации над процессами диссоциации. Они характеризуются следующими силами ММВ: FA-A FA-B, FB-B FA-B 2-й подкласс. Жидкости неограниченно растворимы друг в друге и образующие смеси с минимумом Ткип и максимумом давления пара. 3-й подкласс. Жидкости неограниченно растворимы друг в друге и образующие смеси с максимумом Ткип и минимумом давления пара. Полностью смешивающиеся жидкости Такие жидкости полностью растворяются одна в другой в любых отношениях, образуя гомогенную смесь, или раствор. Для изучения таких систем, как, впрочем, и других растворов жидкостей в жидкостях, используются диаграммы давление-состав или температура кипения-состав. Эти диаграммы были впервые предложены Д.П. Коноваловым. На этих графиках используются две оси ординат, на которых наносятся Ткип или рнас. пара, а на оси абцисс – содержание жидкостей А и В в мольных долях. Начнем рассмотрение таких систем с модели идеального раствора, хотя такие системы являются абстракцикй и их реально не существует. Но некоторые растворы (в основном те, у которых молекулы похоже), тем не менее, близки к идеальным: бензол-толуол, смесь алканов в сырой нефти, гептан-гексан, этиловый спирт – метиловый спирт и т.д. Свойства идеального раствора. Идеальные растворы подчиняются закону Рауля (напоминание виде слайда). Пар идеального раствора можно рассматривать как идеальный газ и он подчиняется закону Дальтона (напоминание виде слайда): полное давление пара двухкомпонентного раствора равно сумме парциальных давлений. В общем случае состав пара отличается от состава жидкого раствора, из которого он получен. При невысоких давлениях пар можно рассматривать как смесь идеальных газов. Состав паровой фазы определяется по формуле (напоминание в виде слайда): (Х1/Х2)п = (P10/P20) (X1/X2)ж Из уравнения следует, что состав паровой фазы одинаков с составом жидкого раствора только в случае равенство давлений пара над чистыми растворителями. Во всех остальных случаях даже для идеальных растворов состав пара отличается от состава раствора. По этой формуле можно вычислить давление пара для многих идеальных растворов или близких к ним, например, бензол-толуол, гексан-гептан, метанол-этанол. Для неидеальных систем состав пара определяется экспериментальным путем. Для равновесия пар - жидкий раствор применяется два типа диаграмм состояния: 1) диаграмма давление пара - состав (Т=const), 2) диаграмма температура кипения - состав (Р=const) Рассмотрим диаграмму кипения для некого реального раствора при постоянном давлении. На этой диаграмме фигуративные точки tA0 и tB0 соответствуют температурам кипения чистых жидкостей А и В. Фазовые диаграммы полностью смешивающихся жидкостей На практике часто возникает необходимость разделить жидкие растворы на составляющие их компоненты. Наиболее распространенные методы разделения жидких однородных растворов состоящих из летучих компонентов - это перегонка и ректификация. Эти методы широко применяют в промышленности: спирто-водочное производство, перегонка нефти (производство керосинов и бензинов), производство ароматических веществ и т.д. Теоретической основой разделения жидких растворов, состоящих из летучих компонентов являются законы Гиббса-Коновалова. Эти законы были теоретически обоснованы Гиббсом и независимо открыты экспериментально Д.П. Коноваловым. Законы Гиббса-Коновалова устанавливают связь между составом жидкого раствора смеси летучих компонентов и составом насыщенного равновесного с ним пара в зависимости от температуры и давления.. В равновесной двухкомпонентной системе сумма мольных долей компонентов в в жидкой (NАж, NBж) и паровой (NАп, NBп) фазах равна единице, т.е. NАж + NBж = 1, NАп + NBп = 1 Эти условия и весь ход дальнейших рассуждений справедливы для жидких растворов двух летучих компонентов, причем пар, находящийся в равновесии с жидким раствором, содержит оба компонента. Летучим компонентом является жидкость, которая при данной температуре имеет достаточно высокое давление пара. К числу жидких растворов из летучих компонентов относятся продукты перегонки нефти (бензины, керосины и др.), продукты спирто-водочного производства. Составы жидкости и находящегося с ней в равновесии пара не совпадают. NАж, NАп NBж NBп Эти неравенства отражают суть первого закона Гиббса-Коновалова. Для уяснения особенностей этого закона обратимся к рисунку. В соответствии с правилом фаз Гиббса в двухкомпонентной (бинарной) равновесной системе: С = 4 - Ф из 4 параметров (температура, давление, составы обеих фаз) только два является независимыми (Т и р). При заданных значениях Т и р в равновесии находится жидкость и пар, обе фазы при этом имеют фиксированный состав. Если же из двух независимых величин одна не изменяется (p=const или T=const), то температура в первом случае и давление во втором однозначно определяется составом любой из сосуществующих фаз. Равновесие между раствором и паром удобно рассматривать в виде диаграмм, выражающих зависимость от состава системы температуру кипения жидкости (при p=const, рис 1. а) или давления пара (при T=const, рис. 1. б). На диаграмме состояния по оси абцисс справа налево отложена мольная доля компонента, имеющего в чистом виде более низкую температуру кипения (для рис. 1. а tA0 tB0), и более высокое давление пара (рис 1. б - pA0 pB0). Концевые точки на оси абцисс соответствуют чистым компонентам NA=1, tA0, pA0, NB=1, tB0, pB0. У раствора мольная доля изменяется в диапазоне 0 N 1. На рисунках следует различать кривую пара, обозначенную «п» и кривую жидкости «ж». «Фигуративные точки», лежащие на кривой жидкости, характеризуют состав кипящей при данной температуре жидкости (а) или состав жидкости, кипящем при данном давлении (б). Фигуративные точки на кривой пара позволяют определить состав пара при тех же условиях. Кривые пара и жидкости разделяют диаграмму состояния на 3 области. Две из них, области пара I и области жидкости III являются гомогенными, а область II отражает гетерогенное состояние системы. В гомогенных областях согласно правилу фаз Гиббса С=К-Ф+2, двухкомпонентная система имеет две степени свободы: состав-температура (при p=const, рис. 1. а) и состав - давление (при t=const, рис. 1 б). Воспользовавшись диаграммами на рисунке определим состав жидкости и пара. Для этой цели проведем на диаграмме прямые tп – tж и рп – рж, параллельные оси абцисс и характеризующие температуру кипения и парциальное давление насыщенного пара системы. Фигуративные точки пересечения этих прямых с кривыми пара и жидкости tп и рп и соответственно, tж и рж будут определять равновесный состав пара и жидкости двухкомпонентной системы. Анализ этих составов показывает, что работает первый закон закон Гиббса-Коновалова: Первый закон Гиббса-Коновалова Закон справедлив как для идеальных, так и реальных растворов. В условиях равновесия относительное содержание компонента в паровой фазе отличается от содержания этого компонента в жидком растворе; В паре содержится больше того компонента, добавление которого в раствор понижает температуру кипения или повышает давление насыщенного пара Пар обогащается более летучим компонентом Д 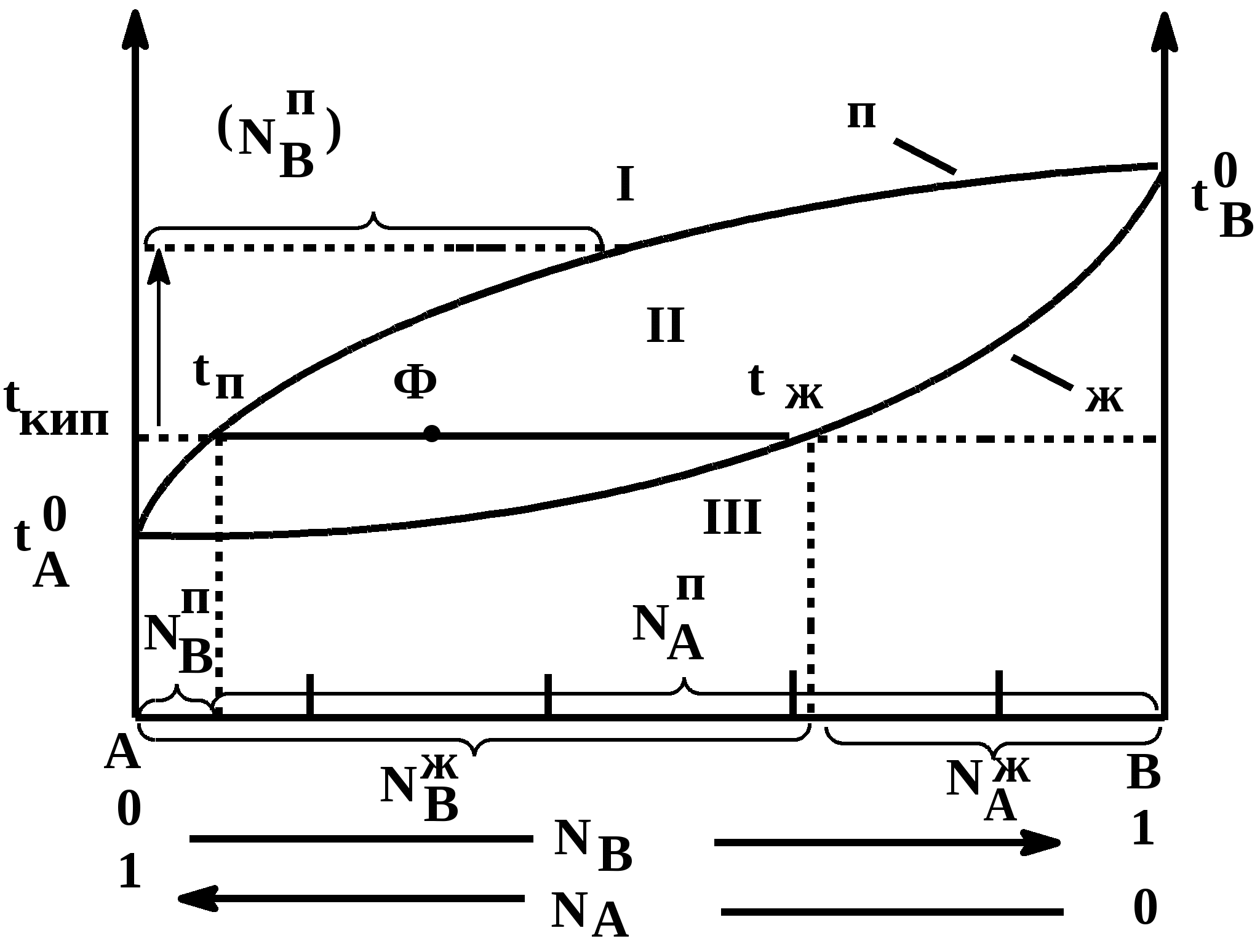 иаграммы, представленные на рисунках справедливы для растворов, подчиняющихся закону Рауля или по крайней мере при незначительном отклонении от этого закона. Причем, зависимости температуры кипения и давления пара от состава системы имеют противоположный вид, являясь зеркальным отображением. а) 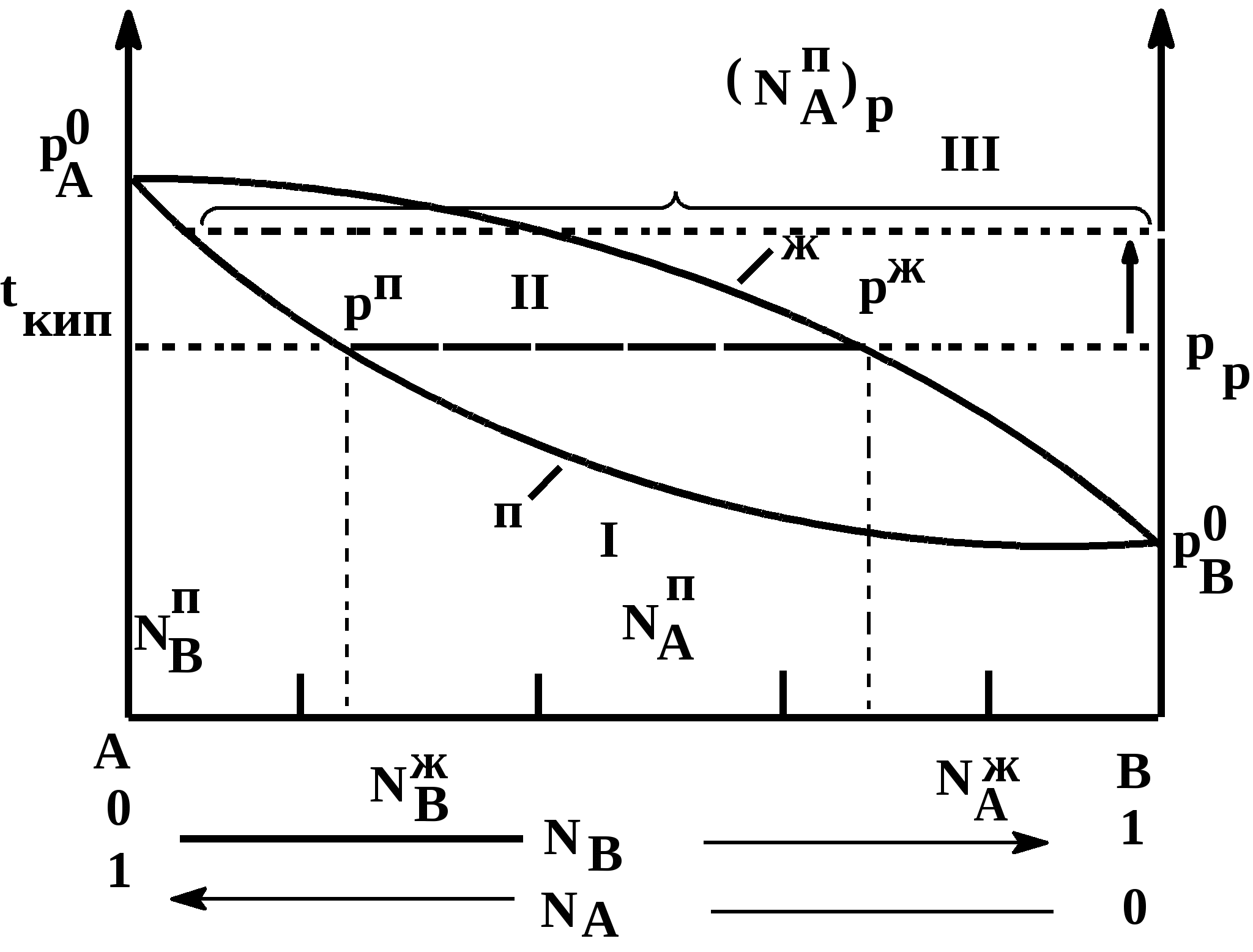 б) Рис. 1. Диаграммы состава «жидкость – пар» двухкомпонентной системы при постоянном давлении (1 а) и постоянной температуре (1 б) (ж, п – кривые состава жидкости и пара, соответственно; I – паровая фаза, II – пар+жидкость, III – жидкая фаза Диаграммы, представленные на рис. 1 а и б справедливы для растворов, близким к идеальным и подчиняющихся закону Рауля или, по крайней мере, при незначительных отклонениях от этого закона. У приведенных на этом рисунке диаграмма отсутствует максимумы и минимумы, что характерно для идеальных или близких к ним растворов. В случае больших отклонений от законов Рауля (рис. 2) на диаграммах состояния пояляются максимумы и минимумы. Н 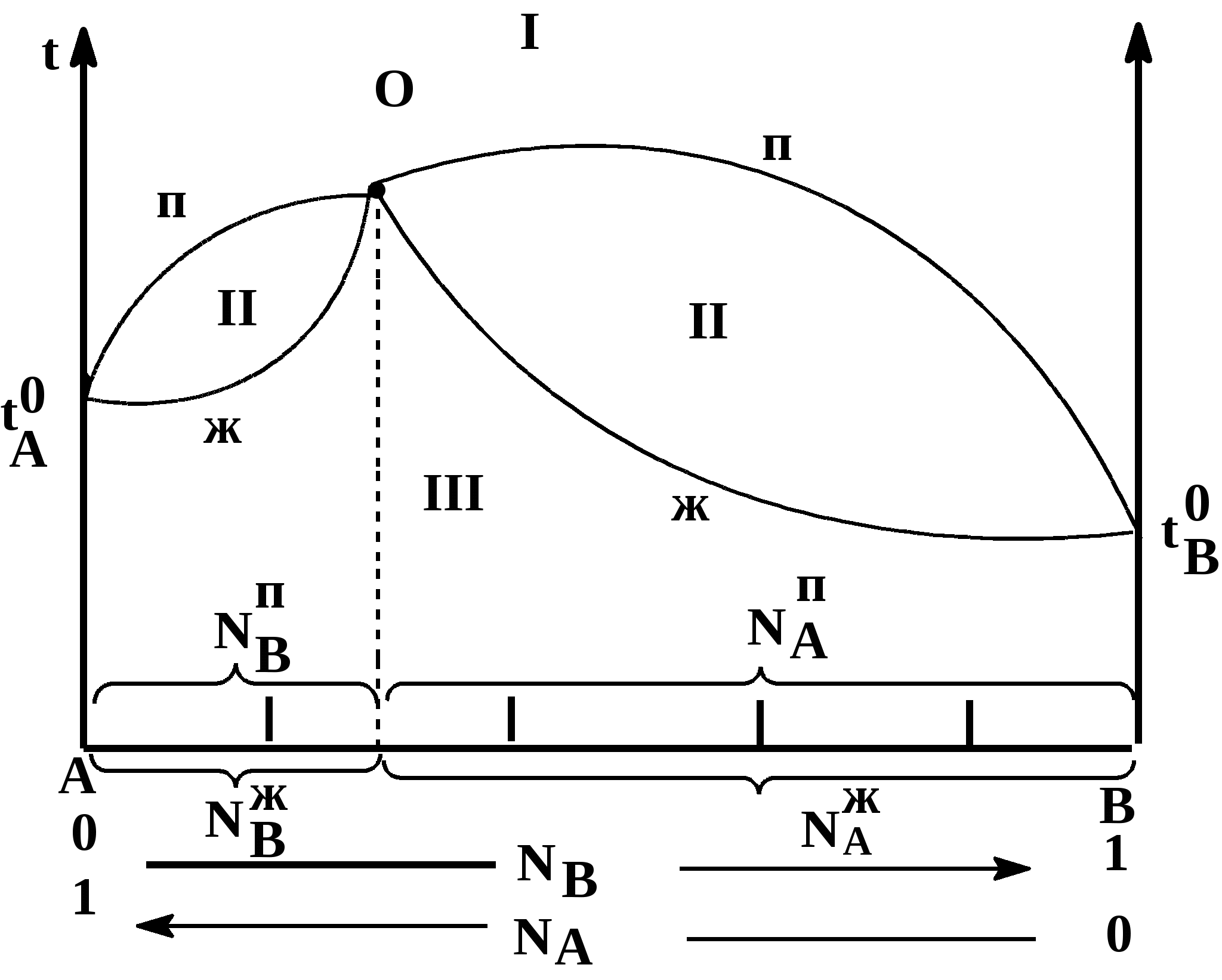 а рисунке 2 а приведена диаграмма соответствующая максимуму температуры кипения в точке О, а на рис. 2 б – минимуму давления пара на диаграмме p-N. Возможен и другой вариант, когда минимуму на кривой температуры кипения соответствует максимум на кривой давления. В любом из вариантов на подобных диаграммах имеются азеотропные точки, в которых состав жидкости и пара одинаков и в которых согласно равенству, NАп=NАж, NBп=NBж имеет место существование соответствуют нераздельно кипящей смеси. Азеотропные смеси – это растворы, при испарении которых получается пар того же состава, что и исходная жидкая смесь (Хп=Хж). Азеотропные смеси – условно инвариантные системы. В реальных растворах азеотропная смесь имеет самую низкую или самую высокую температуру кипения. Приведем сведения о составе (%) некоторых систем в азеотропных точка и температуре кипения растворов азеотропного состава: вода (95.57)-этиловый спирт (4.43) – 78.13оС; вода (12.10)-изопропиловый спирт – 80.37 оС, этиловый спирт (32.37)-бензол (67.63) –68.24 оС, сероуглерод (66.0)-ацетон(34.0) – 39.25 оС. 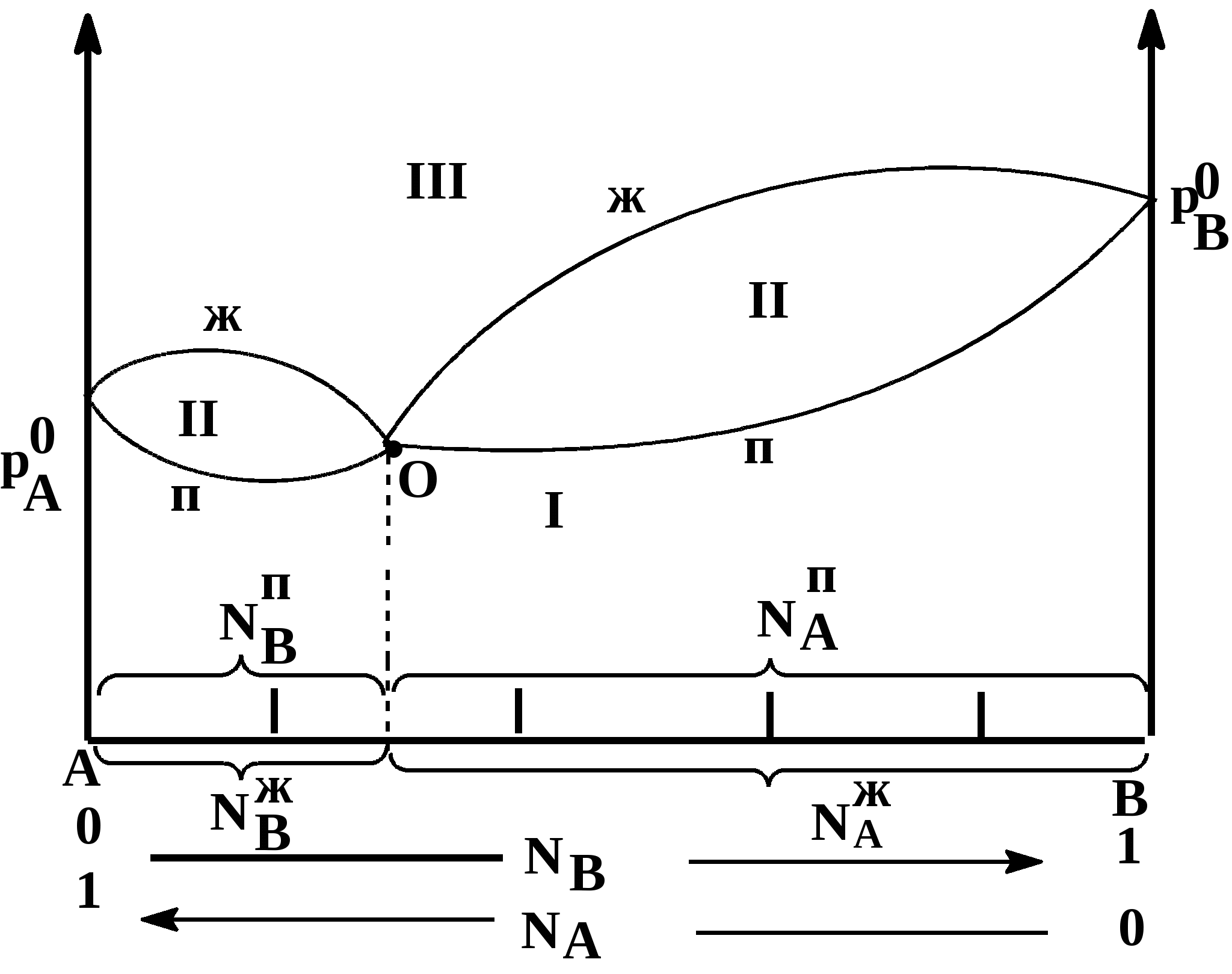 Диаграммы состояния, характеризующаяся наличием азеотропной точки, подчиняются второму закону Гиббса-Коновалова. Как и первый закон он имеет несколько формулировок. Приведем одну из них, наиболее часто встречающуюся и более общую: Точки экстремума на кривых температуры кипения (p=const) или на кривых давления (t=const) соответствуют растворам, состав жидкости которых одинаков с составом равновесного с ней пара. В условиях равновесия азеотропная смесь испаряется как чистое вещество. Законы Гиббса-Коновалова справедливы вдали от критического состояния (когда находящиеся в равновесии жидкость и ее насыщенный пар становятся тождественными по всем параметрам). К параметрам, которые характеризуют критическое состояние и называются критическими, относятся температура (647.3К), давление (221,206 105 Па), состав системы и мольный объем (56 10-6 м3/моль). За пределами критических параметров равновесие фаз системы нарушается и она из гетерогенной превращается в гомогенную. КРИТИЧЕСКОЕ СОСТОЯНИЕ - в физике - состояние двух равновесно сосуществующих фаз, при достижении которого фазы становятся тождественными по своим свойствам. Критическое состояние характеризуется критическими значениями температуры, давления, удельного объема, развитием флуктуаций. В критическом состоянии системы жидкость - пар удельные объемы жидкой и паровой фаз становятся одинаковыми, теплота фазового перехода обращается в нуль, исчезают граница раздела фаз и поверхностное натяжение. Поэтому критическое состояние можно рассматривать как предельное состояние однофазной системы. Сжимаемость системы жидкость - пар в критическом состоянии очень велика, вследствие чего резко возрастают флуктуации плотности и наблюдается критическая опалесценция. Первоначально законы Гиббса-Коновалова рассматривались применительно к двухкомпонентным системам, образующим жидкую и паровую фазы. Впоследствие было установлено, что эти законы можно распространить и на многокомпонентные системы. Законы Вревского Законы, предложенные М.С. Вревским, отражают поведение растворов жидкостей, образующих азеотропы, с изменением р и Т. Эти законы описывают влияние температуры и давления на состав пара азеотропной смеси в зависимости от мольной теплоты испарения компонентов раствора. Эти законы дополняют законы Коновалова. О трудах Д.П.Коновалова и М.С.Вревского, во главе с которыми петербургская термодинамическая школа вошла в первую четверть ХХ в., нужно сказать особо. Помимо других своих работ они открыли по три закона, описывающие фазовое равновесие в бинарной системе жидкость – пар. Законы Коновалова вошли в мировую литературу прочно, хотя бы один из них (обычно первый) можно найти в любом учебнике по термодинамике. Соответственные законы Вревского менее известны (их современный вывод дан А.В.Сторонкиным), хотя их практическое значение не менее велико.Согласно первому закону Коновалова, при заданном давлении температура кипения раствора возрастает с концентрацией менее летучего компонента. Первый же закон Вревского гласит, что при заданном составе раствора повышение температуры ведет к обогащению пара менее летучим компонентом (парциальная молярная теплота испарения которого больше). Эти законы описывают поведение одной и той же системы при различных внешних условиях: закон Коновалова при постоянстве давления, а закон Вревского при постоянстве состава раствора. Оба закона справедливы лишь вдали от критической точки. ВРЕВСКИЙ Михаил Степанович (1871-1929) , российский физикохимик, член-корреспондент АН СССР (1929). Основные труды по термодинамике растворов. Установил (1911) законы, выражающие зависимость состава пара раствора от теплоты испарения его компонентов и температуры (законы Вревского). Премия им. В. И. Ленина (1929). Первый закон Вревского гласит, что при фиксированном составе жидкой фазы равновесная с ней газовая (паровая) фаза обогащается с увеличением температуры (давления) тем компонентом, для которого больше мольная теплота испарения. Первый закон Вревского справедлив для любых летучих смесей, в независимости от того, образуют ли они или не образуют азеотропные смеси. Второй закон гласит, что при повышении температуры (давления) в азеотропной смеси с максимумом температуры кипения и минимумом давления пара (то что у нас на рисунке 2 а и б) увеличивается содержание компонента, обладающего меньшей мольной теплотой испарения. В обратном случае возрастает содержание компонента с большей мольной теплотой испарения. Термодинамическое обоснование законов Гиббса-Коновалова Как уже было отмечено, эти законы были открыты Коноваловым, а Гиббс дал им теоретическое обоснование. Для идеальных жидких растворов, состоящих из двух компонентов (А и В), пар которых также можно считать идеальным газом, согласно закону Рауля можно написать: pA = NAж pA0; pB = NBж pB0; NBж = pB0(1- NAж) поделив одно на другое 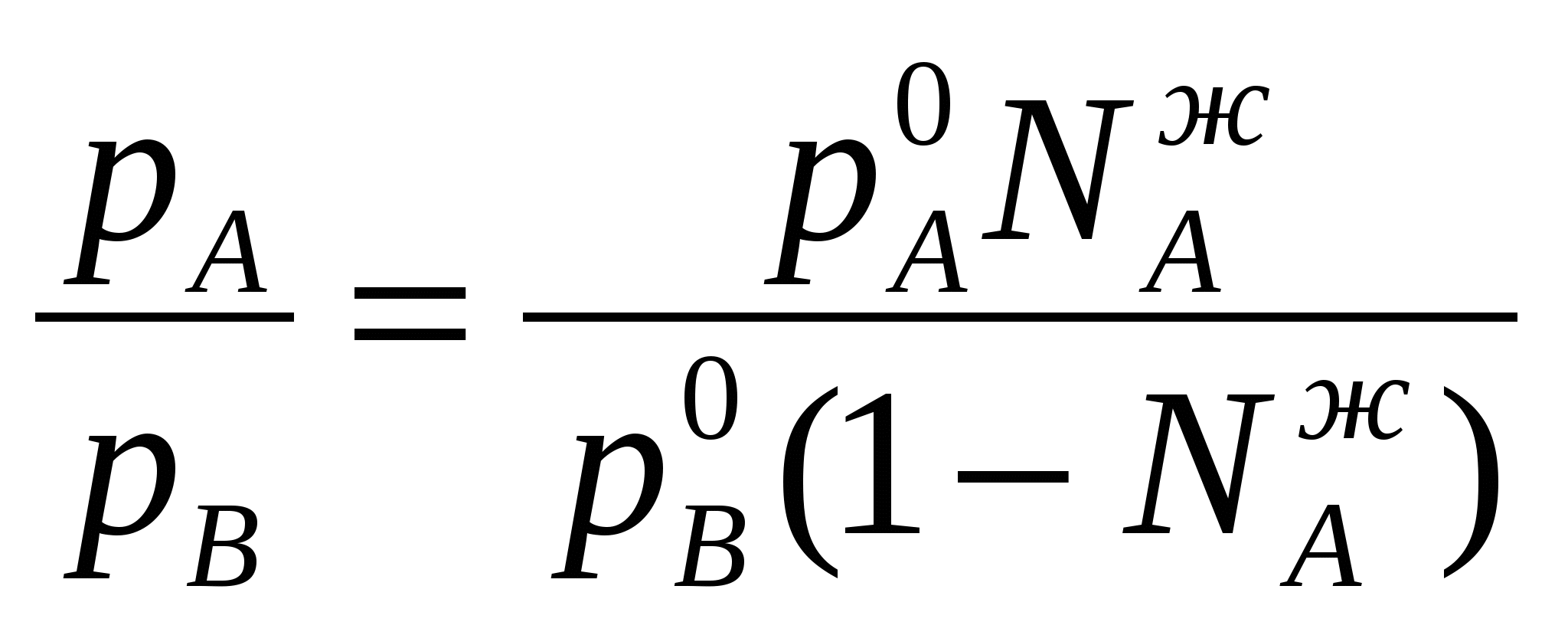 Из уравнения состояния можно определить мольную долю компонента А в паровой фазе: pAV=NAпRT, pBV=NBпRT=(1-NAп)RT 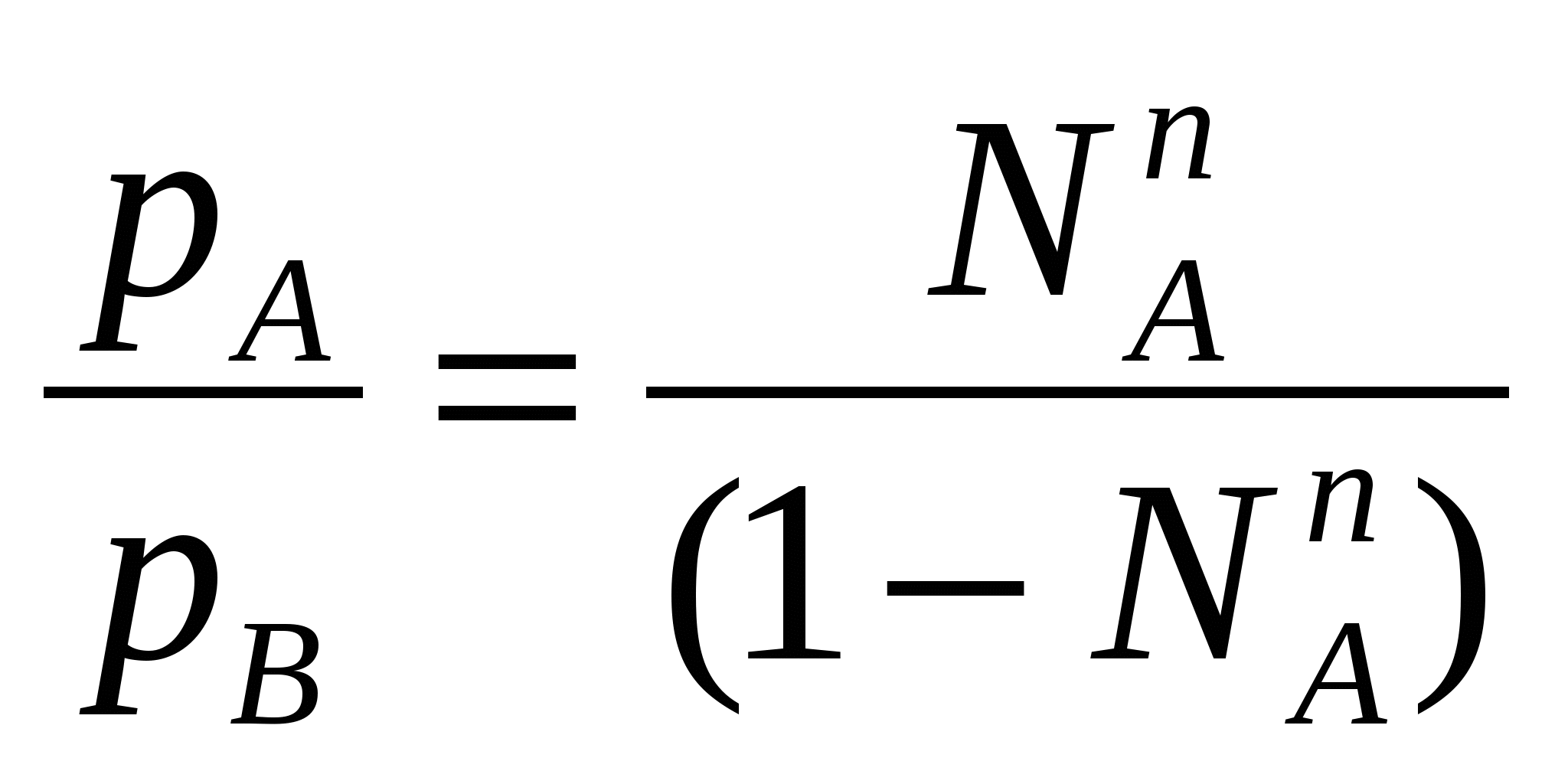 Приравнивая правые части уравнений и комбинируя получим: 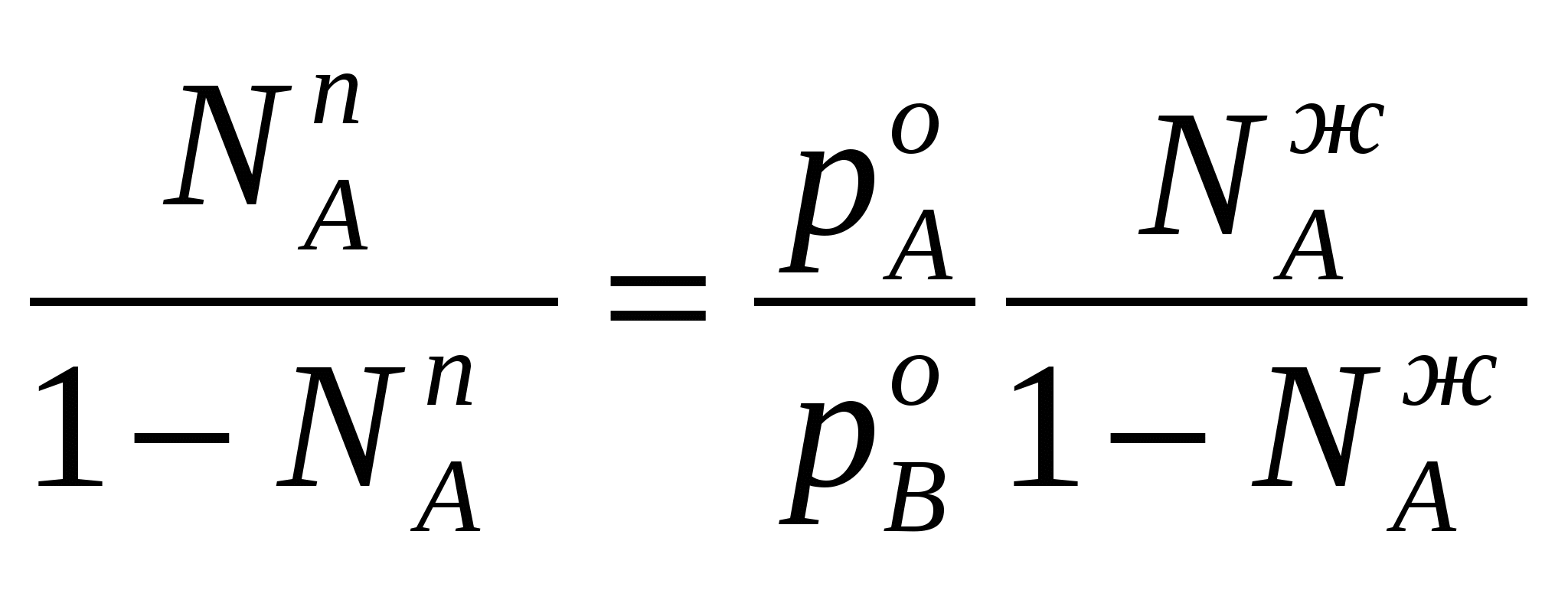 Уравнение показывает изменение состава жидкости и пара в соответствии с законами Гиббса-Коновалова. Действительно, если давление пара вещества А больше давления пара вещества В (А более летуче), то NAп/NBп NAж/NBж, т.е. пар обогащен более летучим компонентом – что соотвтетствует первому закону Гиббса-Коновалова. Если рА = рВ, то NAп/NBп = NAж/NBж Это соответствует азеотропной точки и для нее составы пар и жидкости одинаковы. К термодинамическому обоснованию законов Гиббса-Коновалова можно подойти, используя уравнение Дюрема-Маргулиса. Уравнение Дюрема-Маргулиса: На основании второго закона Гиббса-Дюгема можно записать: nAdA + nBdB = 0 или NAжdA + NBжdB = 0 поскольку химический потенциал можно выразить через парциальное давление компонента раствора = 0 + RTlnp d = RTdlnp NBжdlnpB = -NAжdlnpA или (1-NAж) (dpB/pB) = -NAж (dpA/pA) Окончательно имеем уравнение Дюрема-Маргулиса: dpB = - NAж/(1- NAж) (pВ/pA) dpA Давления (pA, pВ) можно связать по закону Дальтона (p = pA + pВ) можно связать с составом паровой фазы: pВ = (1-NAп)p и pA = NAпp dp = dpB + dpA dp = [1 - NAж/(1- NAж) (1- NAп)/ NAп] dpA Делим на dNAж (dp/ dNAж) = [1 - NAж/(1- NAж) (1- NAп)/ NAп] (dpA/ dNAж) С ростом концентрации компонента А его парциальное давление растет и увеличивается на (dpA/dNAж). Растет и общее парциальное давление. При (dp/ dNAж) 0, NAп NAж, т.е. пар обогащен более летучим компонентом. Это соответствует первому закону Гиббса-Коновалова. Для определения экстремума на кривой необходимо предположить, что (dp/ dNAж) = 0, что будет означать, что NAп = NAж, что характерно для азеотропных точек в соответствии со вторым законом Гиббса-Коновалова. Это уравнение позволяет определить связь между изменением парциального давления компонента (pA, pВ) и составом раствора (NAж). С его помощью можно расчитать давления пара одного из компонентов раствора, если известно давление пара другого компонента и состав раствора. При его выводе не делалось никаких допущений относительно свойств жидкости и паровой фазы. В связи с этим уравнение Дюрема-Маргулиса выражает коллективные свойства раствора и справедливо для любого двухкомпонентного жидкого раствора, образованного летучими компонентами. 3аконы Вревского. 1. Закон, согласно которому при повышении температуры раствора его пар обогащается тем компонентом, парциальная мольная теплота испарения которого больше. 2. Закон, согласно которому если на кривой зависимости общего давления пара от состава раствора имеется максимум, то при повышении температуры в азеотропной смеси возрастает концентрация того компонента, парциальная мольная теплота испарения которого больше; если на этой кривой имеется минимум, то при повышении температуры в азеотропной смеси возрастает концентрация того компонента, парциальная мольная теплота испарения которого меньше. 3. Закон, согласно которому если на кривой зависимости общего давления пара от состава раствора имеется максимум, то при изменении температуры состав пара, находящегося в равновесии с раствором постоянного состава, и состав азеотропной смеси изменяются в одном направлении; если на этой кривой имеется минимум, то соответствующие составы изменяются в противоположных направлениях |
