Скрипко Т.В. Общая и неорганическая химия Практикум. Общая и неорганическая химия

• Название: Общая и неорганическая химия
• Анкор: Скрипко Т.В. Общая и неорганическая химия Практикум.doc
• Дата: 10.05.2017
• Размер: 2.12 Mb.
• Имя файла: Скрипко Т.В. Общая и неорганическая химия Практикум.doc
• Тип: Документы; #7414
• Категория: Химия
• страница: 12 из 17

В задачах 798–812 вычислить произведение растворимости мало­растворимых электролитов

№ задачи	Электролит	Растворимость электролита
798 799 800 801 802 803 804 805 806 807 808 809 810 811 812	Ag3РO4 Мg(ОН)2 АgСl ВаСО3 СаСO3 PbSO4 AgIO3 BaSO4 PbBr2 CaF2 PbCI2 AgBr MgCO3 PbBr2 PbI2	0,0065 г/л 0,012 г/л 0,0018 г/л 8,9·10-5 моль/л 1,3·10-4 моль/л 0,132 г в 3 л 0,176 г Ag+ в 3 л 2,3·10-3 г/л 2,7·10-2 моль/л 2·10-4 моль/л 11 г/л 1,1·10-4 г/л 2,67·10-3г/л 0,0427 г/л 1 г в 1470 мл воды

В задачах 813-824 вычислить растворимость электролита по величине произведения растворимости (прил. табл.8)

№ задачи	Электролит	№ задачи	Электролит	№ задачи	Электролит
813 814 815 816	ВаСгО4 Ag2SO3 AgSCN SrCrO4	817 818 819 820	CaC2O4 CaSO4 Ag2CrO4 Ag2CO3	821 822 823 824	Сu(ОН)2 СuS BaF2 PbI2

5.7. Гидролиз солей

Гидролиз солей относится к обменным реакциям, поскольку процесс идет без изменения степени окисления реагирующих веществ. Сущность реакций гидролиза состоит во взаимодействии ионов соли с ионами водыс образованием слабых электролитов. В процессе гидролиза один из ионов воды связывается в слабый электролит, а другой, как правило, накапливается в растворе. Тот ион, который накапливается в растворе, определяет реакцию среды. Если накапливаются ионы Н⁺, то среда будет кислой, если группы ОН – щелочной. При образовании одинаковых по си­ле электролитов среда может быть и нейтральной. Последний случай встречается редко.

Уравнения гидролиза пишутся аналогично другим ионным уравнениям: малодиссоциированные (в том числе и вода) и малорастворимые, а также газообразные вещества пишутся в виде молекул, сильные электролиты записываются в виде ионов. Уравнения гидролиза солей многоосновных кислот и многокислотных оснований записываются по ступеням, аналогично ступенчатой диссоциации.

Гидролиз солей, или их обменное взаимодействие с водой, происходит лишь в тех случаях, когда ионы, образующиеся в результате электролитической диссоциации соли–катион, анион или оба вместе, способны образовывать с ионами воды Н⁺ и ОН^– – малодиссоциированные сочетания. Гидролизу подвергаются соли, образованные: слабыми кислотами и сильными основаниями; слабыми основаниями и сильными кислотами; слабыми кислотами и слабыми основаниями.

Если процесс гидролиза необходимо усилить, то следует разбавить раствор и повысить температуру.

Если необходимо уменьшить гидролиз солей, то к раствору добавляют кислоту или щелочь в зависимости от типа гидролизуемой соли.
Примеры составления задач и их решения

Задача 858

Какие из перечисленных ниже солей подвергаются гидролизу: NH₄I, Na₂S, Al(CH₃COO)₃, CaCl₂?

Решение:

Иодид аммония - соль, образованная сильной кислотой и слабым основанием. Гидролиз соли: гидролизу подвергается катион соли. Реакция раствора кислая: рН<7.
NH₄I + HOH  NH₄OH + HI.

Или в ионном виде:

NH₄⁺ + HOH  NH₄OH + H⁺.
Сульфид натрия – соль, образованная сильным основанием и слабой кислотой.

При растворении солей многоосновных кислот гидролиз протекает ступенчато:

Na₂S + H₂O  NaHS + NaOH.
Или в ионной форме:

S^2– + H₂O  HS^– + OH^–.

Гидролизу подвергается анион соли. Процесс отражает гидролиз по первой стадии.

Чтобы гидролиз соли многоосновной кислоты прошел полностью, как правило, увеличивают температуру процесса:

,

или в ионной форме: .

Раствор такой соли проявляет щелочную реакцию рН7.

Ацетат алюминия – соль, образованная слабым основанием и слабой кислотой. Гидролизу подвергается как катион, так и анион соли:

Al(CH₃COO)₃ + H₂O  AlOH(CH₃COO)₂ + CH₃COOH.

Параллельно идут два процесса:

Al³⁺ + H₂O  AlOH²⁺ + H⁺,

CH₃COO^– + H₂O  CH₃COOH + OH^–.

В этом случае реакция раствора зависит от относительной силы кислоты и основания, образующих соль. Для гидролиза А1(СН₃С00)₃ реакция полученного раствора будет слабокислотной, поскольку константа диссоциации А1(OН)₃ (К=1,3810^-9) меньше константы диссоциации уксусной кислоты (К=I,7510^-5).

Хлорид кальция - соль, образованная сильным основанием и сильной кислотой. Взаимодействие с водой можно представить таким образом:

CaCl₂ + 2H₂O Ca(OH)₂ + 2HCl,

H₂O  H⁺ + OH^–.

Однако единственным малодиссоциирующим соединением в реакции остается сама вода, следовательно, равновесие реакции полностью смещено влево - гидролиз не идет. Раствор соли проявляет нейтральную среду.

Реакция гидролиза представляет собой эндотермический процесс. Поскольку гидролиз является обычным равновесным процессом, то он за­висит от всех тех факторов, которые влияют на равновесие реакций, и к нему применимо правило Ле-Шателье.
Задача 864

Вычислить константу гидролиза NН₄Сl.

Решение:

Гидролиз соли, образованной слабым основанием и сильной кислотой, характеризуется константой гидролиза:

,

где - ионное произведение воды; К_осн – константа диссоциации основания.

Из табл. 7 приложения находим = 1,8  10^-5 .

Отсюда

.
Задача 880

Вычислить степень гидролиза ZnCl₂ по 1 ступени в 0,5 М растворе.

Решение:

Ионное уравнение гидролиза

Zn²⁺ + H₂O  ZnOH⁺ + H⁺,

= 1,510^-9.

Степень гидролиза вычисляем по формуле: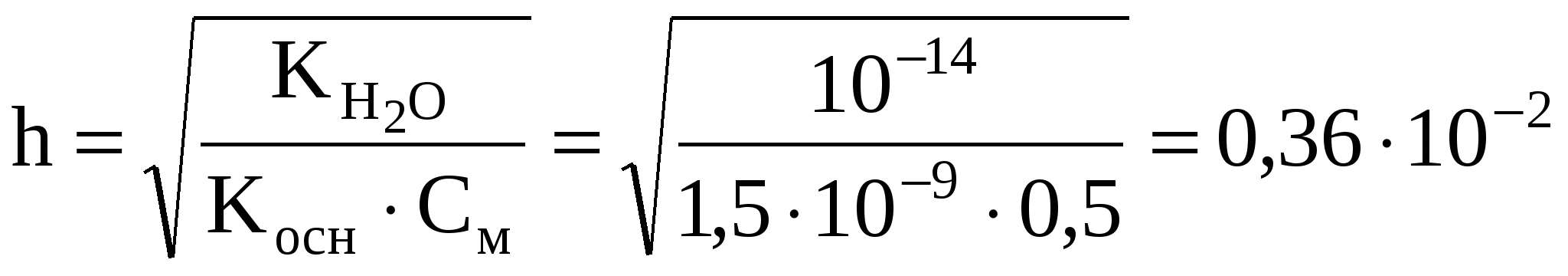
(0,36 %).

Степень гидролиза соли тем больше, чем меньше ее концентрация; иначе говоря, при разбавлении раствора гидролизующейся соли степень ее гидролиза возрастает.

При выполнении заданий рекомендуется использовать методические указания [8].

При решении задач по гидролизу использовать данные констант диссоциации некоторых электролитов, приведенные в табл. 7 приложения.

В задачах 825–858 указать, какие из перечисленных ниже солей подвергаются гидролизу. Для каждой из гидролизующихся солей написать в молекулярной и ионной форме уравнения гидролиза, указать реакцию водного раствора соли

задачи

825 826 827 828 829 830 831 832 833 834 835 836 837 838

CrCI3, Na2S, AI2S3, KNO3 Zn(NO3)2, NaNO2, Ba(NO3)2, (NH4)2S MnSO4, CH3COONH4, KCI, NaHSO3 Na2SiO3, CuSO4, NaBr, Pb(CH3COO)2 NaH2PO4, AI2(SO4)3, NH4CN, BaCI2 Ca(HS2), Fe(CN)2, Ni(NO3)2, NaCI HCOONH4, FeCI3, KHCO3, Li2SO4 (CuOH)2SO4, (NH4)2CO3, K2SO4, Ba(NO3)2 Cr2(SO4)3, K2S, Na2SO4, Cr2S3 Na3AsO4, CoSO4, NaCIO4, Al2S3 CsNO3, K2HAsO4, NH4CIO4, Cu(CH3COO)2 Na2TeO3, ZnSO4, KJ, Fe(HCOO)3 K2HAsO4, NH4Br, RbNO3, Al(CH3COO)3 CaS, SrCl2, MgSO4, (NH4)2SO3

839 840 841 842 843 844 845 846 847 848 849 850 851 852 853 854 855 856 857 858

K2Se, BaJ2, Pb(CH3COO)2, SnSO4 NH4CN, Mg(ClO4)2, Ca(HS)2, RbCl Ca(NO2)2, Li2CrO4, Cr2S3, Zn(NO3)2 (ZnOH)2SO4, NaAsO2, Fe(CN)2, K2SO4 Zn(CN)2, Li2SO3, MnSO4, (NH4)2CO3 Bi(NO3)2, Li2SiO3, KJ, (NH4)2CO3 SbCl3, K2CrO4, Zn(CN)2, CdSO4 CH3COOK, Fe2(SO4)3, BaCl2, Al2S3 Al2S3, CsNO3, NH4ClO4, K2Te K2Te, SnSO4, Cu(CN)2, NaNO3 CuOHCl, NaH2PO4, NaBr, Cu(CH3COO)2 SrS, FeCl3, NH4CN, K2SO4 K2CO3, NaNO2, NH4HCOO, LiCl NaClO3, (NH4)2SO4, CH3COOK, KNO3 CuCl2, Ca(CH3COO)2, Pb(NO3)2, NaBr FeCl3, (NH4)2CO3, Na3PO4, K2CrO4 NaHS, Al2S3, MnCl2, Ba(NO3)2 NaHSO3, MnJ2, (NH4)2S, KSCN NaClO4, Mg(CH3COO)2, Ni3(PO4)2, RbCl NH4J, Na2S, Al(CH3COO)3, CaCl2

В задачах 859–868 вычислить константу гидролиза

859 860 861 862 863

ацетата натрия формиата натрия ацетата калия карбоната калия ортофосфата калия

864 865 866 867 868

хлорида аммония гипохлорида натрия цианида натрия гидрокарбоната калия сульфита калия

В задачах 869–880 вычислить степень гидролиза

№ задачи

869 870 871 872 873 874 875 876 877 878 879 880

Цианида калия в 0,1 Н растворе Ацетата калия в 0,1 М растворе 0,1 М раствора ортофосфата калия Карбоната натрия по I ступени в 0,2 М растворе Ортофосфата натрия по I ступени в 0,1 М растворе В 0,01 М растворе гидрокарбоната натрия Цианида аммония в 0,01Н растворе Хлорида аммония в 0,01 М растворе Гипохлорида калия в 0,001 М растворе В 0,06 М растворе нитрата свинца по I ступени Формиата лития в 0,001 н растворе Хлорида цинка по I ступени в 0,5 М растворе

6. СТРОЕНИЕ АТОМА

Вся совокупность сложных движений электрона в атоме описывается четырьмя квантовыми числами: главным n , побочным ℓ , магнитным m_ℓи спиновым m_S.

Главное квантовое число n определяет общую энергию электрона на данной орбитали и его удаленность от ядра. Оно может принимать любые целые значения, начиная с единицы: 1,2,3,4... . Под главным квантовым числом, равным , подразумевают, что атому сообщена энергия, достаточная для полного отделения электрона от ядра (ионизация атома). N = 2n² – максимальное число электронов, которое находится на каждом энергетическом уровне.

Энергетические уровни представляют собой совокупность некоторых энергетических подуровней. Существование различий в энергетическом состоянии электронов отражается побочным (орбитальным) квантовым числом ℓ. Это квантовое число может принимать целочисленное значение от 0 до n-1 (ℓ = 0, 1, 2 ... n - 1). Численные значения ℓпринято обозначать буквенными символами:

Значение ℓ	0	1	2	3	4
Буквенное обозначение	s	p	d	f	g

В этом случае говорят о s, p, d, f, g, – состояниях элект­ронов, или s, p, d, f, g –орбиталях. Орбиталь – совокупность положений электрона в атоме, т.е. область пространства, где энер­гетически выгоднее всего находиться электрону.

ℓ – определяет форму электронного облака, а также орбитальный момент – момент количества движения электрона при его вращении вок­руг ядра (отсюда и второе название этого квантового числа – орбитальное). Если ℓ = 0 (s -орбиталь), то электронное облако имеет сферическую форму и не обладает направленностью в пространстве. При ℓ = 1(р -орбиталь) электронное облако имеет форму гантели, т.е. форму тела вращения, полученного из "восьмерки". При ℓ = 2 (d- орбиталь) электронное облако имеет четырехлепестковую фигуру. Формы f и g электронных облаков намного сложнее. Максимальное число электронов на подуровне рассчитывается по формуле 2(2ℓ + 1).

Ориентация электронного облака в пространстве не может быть произвольной. Она определяется значением третьего, так называемого магнитного квантового числа m_ℓ.

m_ℓ может принимать значения любых целых чисел, как положительных так и отрицательных от -1до +1, включая 0, т.е. всего (2ℓ + 1) значений. Например, при l = 0 m_ℓ= 0; при ℓ = 1 m_ℓравно -1, 0, +1; при ℓ, равном 3, m_ℓ имеет семь значений (2ℓ + 1 = 2∙3 + 1 = 7): -3, -2, -1, 0, +1,+2,+3 – семь различных ориентаций fэлектрон­ных облаков в пространстве.

m_S – спиновое квантовое число определяет собственное состояние электрона, результат вращения электрона вокруг своей оси. Спиновое квантовое число может иметь два значения: +1/2 или -1/2. Итак, состояние электронов можно описать набором четырех квантовых чисел, но для объяснения строения электронных оболочек атомов нужно знать еще три основных положения: принцип Паули, правило Хунда, принцип наименьшей энергии.

Принцип Паули. В атоме не может быть двух электронов, у которых все четыре квантовых числа были бы одинаковыми.

Правило Хунда. При данном значении ℓ (то есть в пределах определенного под­­­уровня) электроны располагаются таким образом, чтобы суммарный спин был максимальным.

Принцип наименьшей энергии – правило Клечковского: в атоме каждый электрон располагается так, чтобы его энергия была минимальна (что отвечает наибольшей его связи с ядром). Энергия электрона в основном определяется главным квантовым числом n и побочным числом ℓ, поэтому сначала заполняются те подуровни, для которых сумма значений n + ℓ является меньшей (энергия электрона на подуровне 4s меньше , чем на подуровне 3d, так как n + ℓ = 4 + 0 = 4 для 4sи n + ℓ = 3 + 2 = 5 для 3d. Когда для двух подуровней суммы n + ℓ равны, сначала идет заполнение с меньшим значением n (на подуровнях 3d, 4p, 5s n + ℓ = 5 – в этом случае происходит заполнение подуровней сначала с меньшим значением n , т.е. 3d  4p  5s).
Примеры составления условий задач и их решения

Задача 889

Составить электронную формулу атомов Be, As в стабильном и возбужденном состояниях и изобразить орбитали внешнего энергетического уровня.

Решение:

Атом бериллия Be.

Стабильное состояние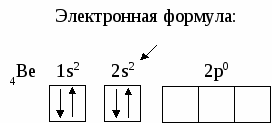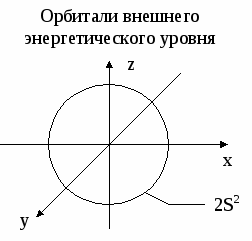



В
Орбитали внешнего энергетического уровня
озбужденное состояние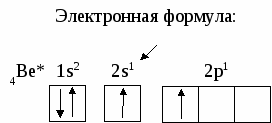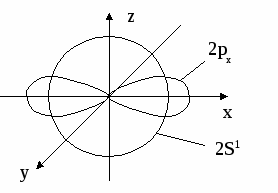






После Sp –гибридизации строение возбужденного атома бериллия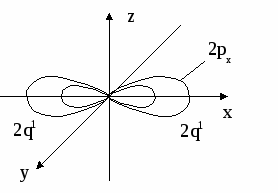



Атом мышьяка As.

Э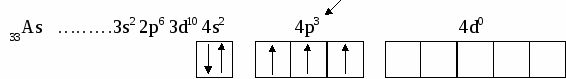лектронная формула: Стабильное состояние

Возбужденное состояние


Электронная формула: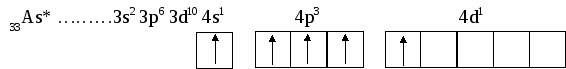



Задача 893

Определить, какие частицы Mg, Si, Al⁺ , S^2– являются изоэлектронными, то есть содержащими одинаковое число электронов. Написать электронные формулы данных частиц.

Решение:

Изоэлектронными являются частицы Mg и Al⁺. Их электронные формулы следующие:

Стабильное состояние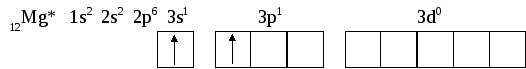

Возбужденное состояние


Возбужденное состояние



Задача 897

Пользуясь правилом Гунда, распределить электроны по квантовым ячейкам, отвечающим низшему и высшему энергетическим состояниям атомов мышьяка As, кобальта Co, стронция Sr.

Решение: