Шпоргалки по статистике. СТАТИСТИКА-шпоры. Общая теория статистики предмет и методы С, основные исходные понятия стат науки

• Название: Общая теория статистики предмет и методы С, основные исходные понятия стат науки
• Анкор: Шпоргалки по статистике
• Дата: 22.11.2022
• Размер: 1.14 Mb.
• Имя файла: СТАТИСТИКА-шпоры.doc
• Тип: Задача; #806510
• страница: 2 из 7

15. Понятие вариация признака, показателей вариации, методы их расчета.

Вариация — это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени. Вариация возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному соче­таются в каждом отдельном случае.

Показатели:

1) Размах вариаций определяется как разность между максимальным и минимальным значение признака. R=Xmax-Xmin.

2) Среднее линейное отклонение. Это показатель в статистике является абсолютной мерой для исчисления вариации.



3) Среднеквадратическое отклонение. Применяется более часто и выражается также в абсолютных величинах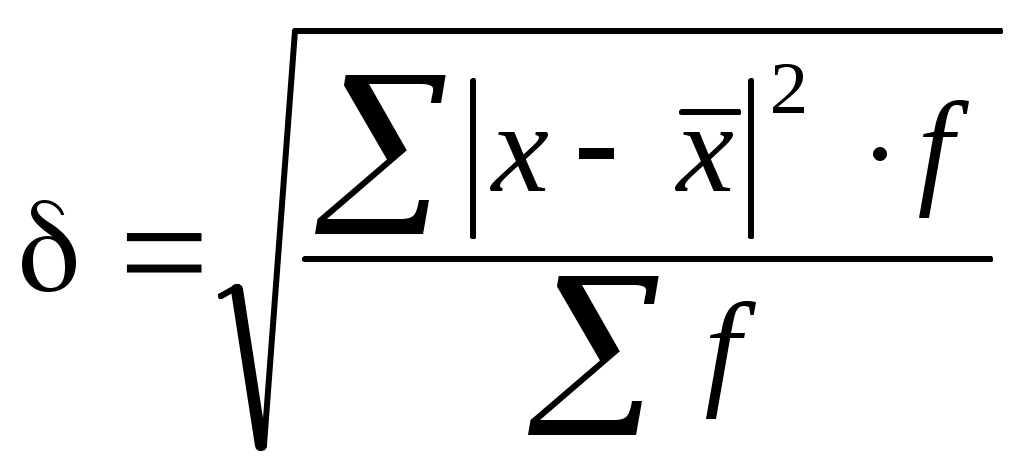


4) Дисперсия представляет собой квадрат среднеквадратического отклонения



5) Коэффициент вариации является относительной мерой степень варьирования признака, который определятся как отношение среднеквадратического отклонения к среднему показателю (в %).



16. Дисперсия, ее свойства и методы расчета

Дисперсия - средний квадрат отклонений индивидуальных значений признака от их средней величины.

Свойства дисперсии:

1. Дисперсия постоянной величины равна нулю.

2. Если все значения признака уменьшить или увеличить на какое-то постоянное число, то дисперсия от этого не изменится.

3. Если все значения признака уменьшить или увеличить в K раз, то дисперсия от этого соответственно увеличится или уменьшится в K2 раз.

4. Сумма квадратов отклонений индивидуальных значений признака x от их средней меньше суммы квадратов отклонений индивидуальных значений признака от любого данного числа a при условии, что , т.е.

Доказано, что эти две суммы отличаются на квадрат разности между и a

5. 
   Дисперсия признака равна разности между средним квадратом значений признака и квадратом их средней, т.е.
   

17. Дисперсия альтернативного признака.

В ряде случаев возникает необходимость измерить вариацию альтернативного признака. Обозначив отсутствие интересующего признака через "0"; его наличие - через "1"; долю единиц, обладающих данным признаком - через q, исчислим среднее значение альтернативного признака и его дисперсию.

Среднее значение альтернативного признака равно



т.к. (сумма долей единиц, обладающих и не обладающих данным признаком, равна единице).

Дисперсия альтернативного признака определяется следующим образом:



Подставив в формулу дисперсии вместо 1-p значение q=1-p, получим:



Таким образом, , т.е. дисперсия альтернативного признака равна произведению доли единиц, обладающих данным признаком, и доли единиц, им не обладающих.

18. Правило сложения дисперсий и его использование в анализе связей.

Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий:



Межгрупповая дисперсияδ² характеризует систематиче­скую вариацию результативного признака, обусловленную влия­нием признака-фактора, положенного в основание группиров­ки. Она равна среднему квадрату отклонений групповых (част­ных) средних X‾iот общей средней X‾ :



Внутригрупповая (частная) дисперсия σ² iотражает случай­ную вариацию, т.е. часть вариации, обусловленную влиянием не­учтенных факторов и не зависящую от признака-фактора, поло­женного в основание группировки. Она равна среднему квадрату отклонений отдельных значений признака внутри группы х от средней арифметической этой группы х) (групповой средней) и может быть исчислена как простая дисперсия или как взвешенная дисперсия по формулам, соответственно: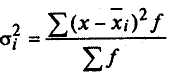

.

19. Сущность выборочного наблюдения, усл-я его примененения.

Выборочное наблюд. – наблюд., при кот. хар-ка всей совок-сти факторов дается по некот. их части, отобранной в случайном порядке (обследование ур-ня жизни дом. хоз-в РБ).

Выборочное наблюд. явл-ся разновид-ю несплошного наблюд-я, при кот. Исслед-ся часть совок-сти. Классиф-я наблюд-я на несплошное и сплошное – это классиф-я по степени охвата ед-ц изучаемой совок-сти.

Выборочное наблюд-е имеет ряд преим-в по сравн-ю со сплошным:

- сокращ-ся затраты времени и ср-в на проведение наблюд-я;

- сокращ-ся число случайных ошибок регистрации

20. Классиф-я ошибок выборочного наблюдения

Расхожд-е между зарегистрированными и действитель­ными значениями изучаемых величин, возникшие в процессе наблюд-я - ошибки наблюд-я.

- Ошибки регистрациивозникают в рез-те неправильной, ошибоч­ной регистрации (записи) ответа на вопрос стат. формуляра.

* Случайные - возникают вследствие действия различных случайных причин (например, описки), они разнонаправленны и в силу действия закона больших чисел часто взаимопогашаются и не оказывают существенного влияния на рез-т стат. наблюд-я.

* Систематические - погрешности, возникающие под действием опред. причин. В случаях, когда эти ошибки имеют место, они существенно искажают рез-ты наблюд-я, напр., приписки в отчетности.

- Ошибки репрезентативности- расхождения между значениями изучаемого признака в выборочной и генеральной совок-сти.

* Случайные - возникают в рез-те того, что выборочная совок-ть недостаточно точно воспроизводит (репрезентует) всю совок-сть в целом, т.е. генеральную совок-сть.

* Систематические - возникают вследствие нарушения пр-па случайности отбора ед-ц в выборочную совок-ть из генеральной.

После окончания стат. наблюд-я собранные мат-лы д.б. тщательно проверены. К-лю подвергаются полнота и кач-во полученных мат-лов.

К-ль полноты — проверка сведений о всех единицах наблюд-я.

К-ль кач-ва полученных мат-лов осущ. с по­м. логического и счетного (арифм-го) к-ля.

Логический контроль - сопоставление ответов на взаимосвязанные вопросы формуляра наблюд-я с целью выявления их логической несовместимости.

К-ль счетный, или арифметический - проверка различных арифм-х расчетов, рез-ты кот. приведены в формуляре наблю­дения (итогов, %-в, ср. величин).

21. Теоретич. основы выборочного наблюд-я.

Выборочный м-д (наблюдение) – один из осн. видов несплошного наблюд-я, при кот. отбор ед-ц осущ-ся на случайной основе. Это вид наблюд-я, при кот. исслед-ся часть совок-ти, взятая на выборку, а получ-е рез-ты распростр-ся на всю совок-ть.

Сущ. неск-ко осн. сп-бов формир-я выборочной совок-ти: собственно случайная выборка; механич. выборка; типическая (районированная) выборка; серийная (гнездовая) выборка; комбинир. выборка; малая выборка.

Отбор ед-ц в выборочную совок-сть м.б. повторным и бесповторным.

22. Виды и сп-бы отбора ед-ц в выборочную совок-ть; расчет ошибок выборки при различных сп-бах отбора

Виды: повторный и бесповторный.

Сп-бы: *собственно случайная выборка; *механич. выборка; *типическая (районированная) выборка; *серийная (гнездовая) выборка; *комбинир. выборка; *малая выборка.


23. Определение объема выборочной совок-ти

Объем выборочной совок-ти – n.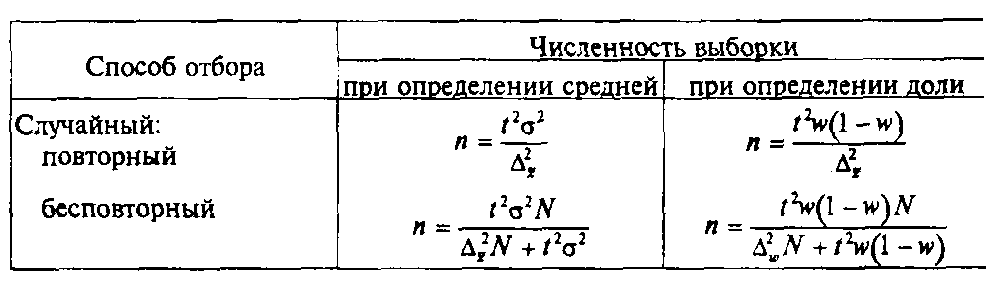



24. Сп-бы распростр-я рез-тов выборочного наблюд-я на ген. совок-ть.

25. Понятие рядов динамики, их виды и правила построения

Ряды динамики- ряды расположенных в хронол. порядке пок-лей, хар-ющих изменение размеров обществ. явлений во времени. Они состоят из 2-х осн. эл-тов:

- моменты или периоды времени (t), к кот. относ. анализируе­мые данные;

- соотв-е им стат. пок-ли, кот. наз. ур-нямидинамич. ряда (у).

Виды:

* абсо­лютных – (исходные (первоначальные) ряды);

- моментные - отдельные их уровни содержат элементы повторного счета.

- интервальные - показатели этих рядов обладают св-вом суммарности.

* относительных и средних величин (производные ряды).

Правила построения:

При построении ряда динамики необх. уровни за каждый период рассчитывать по единой методологиии в одинаковых единицах измерения.

Проблемой постр-я рядов динамики - пробле­ма сопоставимостиих уровней. Показатели динамич. ряда д.б. однородны по эк. содержанию. Проб­лема сопоставимости уровней рядов динамики может решаться либо в процессе сбора и обработки данных, либо путем их пересчета.

Несопоставимость в рядах динамики обусловливается различн. прич-и:

- из-за изменения терри­ториальных границ.

- из-за изменения даты учета, (для получения сопостави­мых данных все уровни д. б. скорректированы по последней дате учета).

- ур-ни интервальных динамических рядов, характеризующие какое-либо явление за различные отрезки времени, вообще не сопоставимы м-ду собой.

Если уровни динамич. ряда измеряются в стоим. ед-­цах, то из-за непрерывного изменения цени применения в стат-ке раз­личных по эк. содержанию видов ценэти данные д.б. приведены в сопоставимых ценах, что осущ-ся либо прямой непосредственной оценкой изучаемого пок-ля в сопоставимых ценах, либо посредством исп-вания соотв-щих индексов цен. То же относится к изменению курса валют.

Ур-ни динамич. ряда д.б. сопост-мы по полноте охватаед-ц набл-я, т.е. в каждом исслед-мом периоде д.б. учтены все ед-цы без каких-либо пропусков.

26. Аналитич. пок-ли динамич. ряда и сп-бы их расчета

Пок-ли: абсолютные приросты; темпы роста; темпы прироста и абсолютное значение (содержание) 1-го % прироста либо снижения.

Расчет этих пок-лей основан на абсо­л. или относ. сравнении ур-ней динамич. ряда. При этом, если каждый ур-нь сравн-ся с его предыд. ур-нем, полу­чают цепныепок-ли, а если каждый ур-нь сравн-ся с начальным или каким-либо другим, принятым за пост. базу сравн-я, то получают базисные пок-ли динамики.

Абсол. прирост- разность 2-х ур-ней ряда динамики. Он показ., на ск-ко абсол. ед-ц данный ур-нь больше или меньше ур-ня, взятого для сравнения, и выража-ся в тех же ед-цах, что и ур-ни анализируемого ряда. М.б. «+» и «–».

Цепной абсол. прирост- разность между сравниваемым ур-нем и предшествующим ему ур-нем.

Базисный абсол. прирост- разность между сравниваемым ур-нем и ур-нем, принятым за пост. базу сравне­ния.

Темп роста– отнош. 2-х ур-ней ряда динамики. Он выраж. в коэфф-х (показ-ет, во ск-ко раз данный ур-нь больше или меньше ур-ня, взятого д/сравнения) или в %-х (ск-ко %-в данный ур-нь составляет по отнош. к др. ур-ню, взятому для сравнения).

Цепной темп роста- отнош. между сравнивае­мым ур-нем и предшествующим ему ур-нем.

Базисный темп роста– отнош. между сравни­ваемым ур-нем и ур-нем, принятым за пост. базу сравн-я.

Темп прироста – отнош. абсол. прироста к ур-ню, при­нятому за базу сравнения. Он показ., на ск-ко %-в ур-нь данного периода больше или меньше базисного.

Темп прироста вычисляется и как разность между темпом роста, выраженным в процентах, и 100 %. М.б. как «+», так и «-».

Абсолютное значение (содержание) 1% прироста (сниже­ния) – отнош. цепного абсол. прироста за анализируемый период к соотв. темпу прироста, выраженному в процентах. Следовательно, количественно абсол. знач. 1% = 1/100 части ур-ня, предшествующего анализируемому, и выражается в тех же ед-цах, что и соотв. ур-ни.

27. Расчет средних величин по данным динамич. ряда

Для обобщ. хар-ки всего ряда динамики в це­лом исп-ся ср. величины: ср. ур-нь, ср. абсол. прирост, ср. темп роста и прироста.

Ср. ур-нь хар-ет типичную величину аб­сол. ур-ней. Он наз. также средней хронологической, или вре­менной средней, и рассчит-ся для разных рядов динамики по-разному.

В интервальных рядах с равными отрезками времени применяется ср. арифм. простая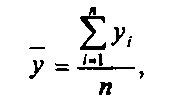



гдеn – число ур-ней ряда.

В интерв-х рядах с неравн. отрезками времени исп-ся арифм. взвешенная



гдеti – продолжительность i-го отрезка времени.

В моментных рядах с равными промежутками между датами ср. ур-нь:



где n – число дат; (n-1) – число равных промежутков времени.

В моментных рядах с неравными промежутками между датами ср. ур. рассчит-ся по ср. арифм. взвешенной



где уi – промежуточная средняя; ti – продолжительность промежутка времени между соотв. датами.

Ср. абсол. приростпоказ., на ск-ко ед-цв среднем увеличивался или уменьшался ур-нь динамич. ряда за соотв. период времени. Он рассчит. по ср. арифм. прос­той из цепных абсол. приростов за послед-ые и равные по продолжит-сти периоды.



где n – число ур-ней ряда динамики; (n-1) – число цепных абсол. приростов.

Ср. темп роста рассчит. по ср. геометрич. из цепных темпов роста, выраженных в коэф-х:

- с равными отрезками времени



где n-1 – число цепных темпов роста;

- с неравными отрезками времени



гдеti – продолжительность соотв. отрезков времени.

Ср. темп приростапоказ., на ск-ко %-вв среднем за ед-цу времени увелич-ся или уменьшался ур-нь ряда динамики. Рассчит-ся как разность между ср. темпом роста и 100% (если в %-х), или 1 (если в коэф-х).

28. Аналитическое выравнивание уровней ряда динамики. Понятие об интерполяции и экстраполяции данных динамического ряда

Более совершенным способом выявления основной тенденции изменений всех уровней динамического ряда является аналитическое выравнивание ряда динамики (определение тренда).Сущность этого способа заключается в нахождении такой аналитической прямой или кривой, ординаты точек которой были бы наиболее близкими к уровням исследуемого динамического ряда, т.е. наилучшим образом отражали бы характер изменения изучаемого явления во времени. Основным содержанием метода аналитического выравнивания в динамических рядах является то, что закономерно изменяющийся уровень изучаемого экономического явления рассчитывается как функция времени (тренд): у, = /(г). Уравнение этой аналитической кривой называется уравнением основной тенденции, или уравнением тренда. Выравнивание по прямой применяется в тех случаях, когда характер движения изучаемого явления ближе всего к прямолинейному. При этом наблюдаются примерно равные постоянные цепные абсолютные приросты. Интерполяцией называется нахождение недостающих промежуточных значений показателей ряда динамики. При этом предполагается, что выявленная закономерность изменения уровней за изучаемый период характерна для его каждого временного отрезка.Экстраполяцией называется определение неизвестных уровней динамического ряда, лежащих за его пределами. Различают перспективную экстраполяцию — продолжение уровней ряда динамики на будущее на основе найденных математических кривых, и ретроспективную экстраполяцию —продолжение уровней ряда в прошлое.