Гл. 1. Общие вопросы аэрогазодинамики

• Название: Общие вопросы аэрогазодинамики
• Дата: 27.02.2022
• Размер: 1.17 Mb.
• Имя файла: Гл. 1.doc
• Тип: Глава; #376002
• страница: 3 из 7

Основные методы и постулаты аэрогазодинамики

Для решения выдвигаемых задач в МЖГ, так же как и в теоретической механике, применяются точные и приближенные приемы интегрирования основных дифференциальных уравнений движения, переноса тепла и др. Для получения суммарных характеристик явлений используются общие теоремы механики. Большая сложность явлений вынуждает МЖГ широко использовать эксперимент, обобщение результатов которого приводит к эмпирическим закономерностям, а иногда и к полуэмпирическим теориям.

Строгая математическая постановка задач МЖГ приводит к сложным системам дифференциальных уравнений в частных производных, решение которых с требуемой точностью возможно только на ЭВМ. Необходимость обобщения результатов расчета и установления простых закономерностей, которые могли, хотя бы только качественно, ориентировать исследователя в его поисках, заставляет продолжать развивать различные приближенные методы, имеющие преимущество наглядности.

Невозможность непосредственного использования уравнений для изучения хаотических (случайных) турбулентных движений жидкости или газа привела к созданию статистических методов исследования.

Гидроаэродинамический эксперимент прочно вошел в обиход лабораторий, НИИ, заводов и вузов. Теоретически изучают лишь простейшие, схематизированные случаи движения жидкости или газа, выясняя на них принципиальную сущность явлений и основные тенденции его развития, а правильность выводов теории проверяют на опыте. Реальные же задачи обычно решаются с помощью эксперимента, позволяющего быстро ответить на конкретные вопросы практики, глубже проникнуть в сущность явления, дополнить и углубить саму теорию. При этом теория учит, как ставить эксперимент, как наиболее точно проводить измерения и обобщать результаты отдельных экспериментов на целые классы явлений. В этом непрерывном взаимодействии теории и эксперимента заключается мощь современной МЖГ, причина ее быстрого развития находится в тесной связи с практическими запросами техники.

Выделим основные предположения и постулаты МЖГ:

1. Справедливость классической механики – механики Ньютона. Это означает, что исследуются движения, скорости которых намного меньше скорости света, и что рассматриваются объекты значительно большие объектов микромира, изучаемых квантовой механикой.

2. Евклидовость пространства. Означает, что физическое действительное пространство, в котором рассматривается течение жидкости или газа, может быть заменено математическим пространством, в котором положение точек определяется с помощью декартовой системы координат и всюду определено расстоянием между точками как

3. Абсолютность времени. Означает, что время течет одинаково для всех наблюдателей независимо от того, двигаются они или нет.

4. Справедливость классической термодинамики. Здесь, в частности, имеется ввиду, что в условиях термодинамического равновесия состояние среды можно определить с помощью нескольких макроскопических параметров (скорость, давление и др.). Если время релаксации (установления термодинамического равновесия) очень мало по сравнению со временем заметного изменения макроскопических параметров газа, то в окрестности каждой точки мы будем иметь дело со средой, находящейся в состоянии термодинамического равновесия.

5. Сплошность среды (непрерывность физических свойств при переходе от одной точки к другой).

Гипотеза сплошности среды. Идеальная

и реальная жидкости
Жидкости и газы, являющиеся объектом изучения МЖГ, обладают двумя основными свойствами: сплошностью и легкой подвижностью или текучестью.

Действительное строение материи, в частности жидкости и газа, – молекулярное. Беспорядочное молекулярное движение, накладываясь на основной поток, значительно его усложняет. Теория не может рассматривать действительность со всей присущей ей сложностью явлений. Теория всегда начинает с упрощения (схематизации) явления, что приводит к модели явления, которая затем кладется в основу исследований.

При изучении практических вопросов силового взаимодействия между газом и находящимся в нем твердым телом (основная задача аэродинамики) можно рассматривать газ как сплошную среду, в которой отсутствуют пустоты, межмолекулярные промежутки и молекулярное движение. Отвлекаясь от молекулярного строения жидкости (газа), можно представить ее как непрерывно распределенную по пространству среду, обладающую физическими свойствами реальной жидкости.

Это предположение называется гипотезой непрерывности, или сплошности, среды (впервые введена в науку Даламбером в 1744 г., а затем Эйлером в 1753 г.).

Гипотеза непрерывности жидкой среды упрощает исследование; она позволяет рассматривать все механические характеристики жидкой среды, каковыми являются скорость, плотность, давление и т. д., как функции координат точки и времени, функции непрерывные и дифференцируемые. Это дает возможность использовать математический аппарат, базирующийся на непрерывных функциях. Молекулярное строение жидкости и газа при этом учитывается через физические свойства среды – плотность, вязкость, теплопроводность и т. д.

Гипотеза о сплошности среды (как и всякая гипотеза) применима в определенных пределах. Она неприменима для сильно разреженных газов, когда длина свободного пробега молекул становится соизмеримой с линейными размерами обтекаемого тела.

При изучении движения тела в газе критерием сплошности среды служит число Кнудсена, равное отношению длины свободного пробега молекул l к характерному размеру телаL (Kn= l / L). В зависимости от значения числа Кнудсена различают следующие режимы течения газа:

Kn < 0,01 – сплошная среда (область обычной газодинамики);

0,01 < Kn < 1 – умеренно разреженная среда, когда возникает так называемое течение со скольжением (скорость потока у стенки не равна нулю, как в сплошной среде, а газ как бы скользит по поверхности тела с конечной скоростью);

1 < Kn < 10 – переходная область от течения со скольжением к свободномолекулярному потоку; здесь необходимо учитывать взаимодействие молекул друг с другом и взаимодействие отраженных от поверхности молекул с молекулами набегающего потока;

Kn > 10 – чрезвычайно большая разреженность среды, когда влияние соударения молекул на величину и направление скорости значительно меньше, чем изменения скорости от соударения молекул с поверхностью тела; газ необходимо рассматривать как свободномолекулярный поток.

В соответствии с гипотезой сплошности в аэрогидродинамике под жидкой частицей понимают не отдельную молекулу, а малый по сравнению с характерными размерами потока или тела элементарный объем .

Физически бесконечно малым объемом называют следующий объем:

1) размеры, которого пренебрежимо малы по сравнению с характерным размером газодинамического течения, так что его средние характеристики не зависят от ;

2) который содержит достаточно много молекул, так что его средние характеристики устойчивы по отношению к (при нормальных условиях куб с ребром, равным 0,001 мм, содержит молекул).

Легкая подвижность или текучесть позволяет ввести понятие вязкости как свойство жидкости и газа оказывать сопротивление при их перемещении. Текучесть есть величина обратная вязкости. У газов, по сравнению с жидкостью, текучесть выше (вязкость ниже).

При дозвуковых и умеренных сверхзвуковых скоростях воздух можно рассматривать как совершенный газ с постоянными удельными теплоемкостями (при гиперзвуке это упрощение неприменимо).

Вязкой жидкостью называют жидкость, при изучении движения которой необходимо учитывать силы внутреннего трения и теплопроводность, обусловленные молекулярным движением.

Жидкость, в которой отсутствуют внутреннее трение и теплопроводность, называют идеальной нетеплопроводной жидкостью. Если при рассмотрении движения реальной жидкости можно пренебречь внутренним трением, то ее можно рассматривать как идеальную.

В газодинамических задачах рассмотрение газа как идеальной жидкости возможно при расчетах распределения давления на поверхности обтекаемых тел и при расчетах распределения температур жидкости на достаточно большом расстоянии от твердой поверхности или от переходных областей.

В действительности реальные газы обнаруживают отклонение от характеристического уравнения идеального газа. Чем выше температура и ниже давление, тем реальные газы по своим свойствам ближе к идеальным. В аэродинамике ЛА воздух с очень высокой точностью описывается моделью идеального газа при числах Маха М 3. Для М 5 можно считать воздух совершенным для расчета давления и нельзя считать его таковым для расчета температуры. При М > 5 модель совершенного газа для воздуха не приемлема. При таких скоростях движения очень сильно возрастает температура вблизи поверхности тела, что приводит к диссоциации, а затем и к ионизации газа. Так при нормальном атмосферном давлении и Т > 2 000 К происходит диссоциация молекул кислорода , а при Т > 4 000 К – диссоциация . Дальнейшее повышение температуры до T К приводит к ионизации газа. Использование при таких условиях модели совершенного газа может привести к ошибке в расчетах Т₀ в несколько раз в сторону ее завышения.

Уравнение состояния
Уравнение состояния для несжимаемой жидкости имеет вид
.
В реальной действительности все жидкости хотя и в малой мере, но сжимаемы, и уравнение состояния имеет более сложную форму. Для идеальных (термодинамически совершенных) газов уравнением состояния является уравнение Менделеева–Клапейрона:

или уравнение Клапейрона , в котором – газовая постоянная для данного сорта газа, где – универсальная газовая постоянная, = 8,314 Дж/моль/К; М – молекулярная масса данного сорта газа, кг/моль. Для смеси газов молекулярная масса зависит от относительной концентрации отдельных компонентов.

Для реальных газов используют уравнения состояния, полученные или эмпирически, или теоретически, или на некоторых частных предположениях относительно внутренней структуры газа. Наиболее известно для реальных газов уравнение состояния Ван-дер-Ваальса: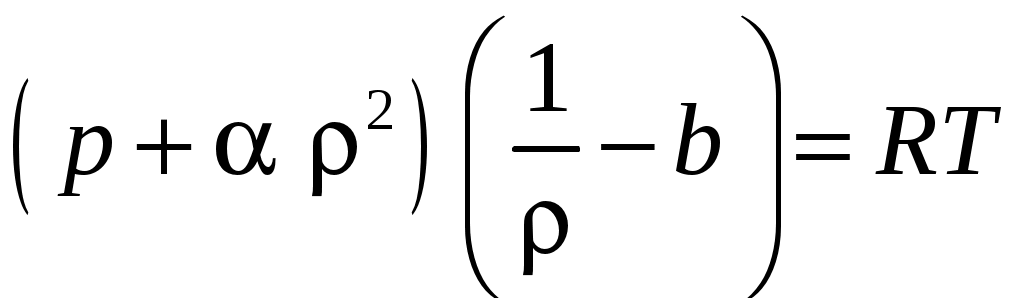
,
где коэффициент характеризует силы взаимодействия между молекулами; b – собственный объем молекул. Коэффициенты и b зависят от температуры.

Для пара чаще всего используют уравнение состояния Молье: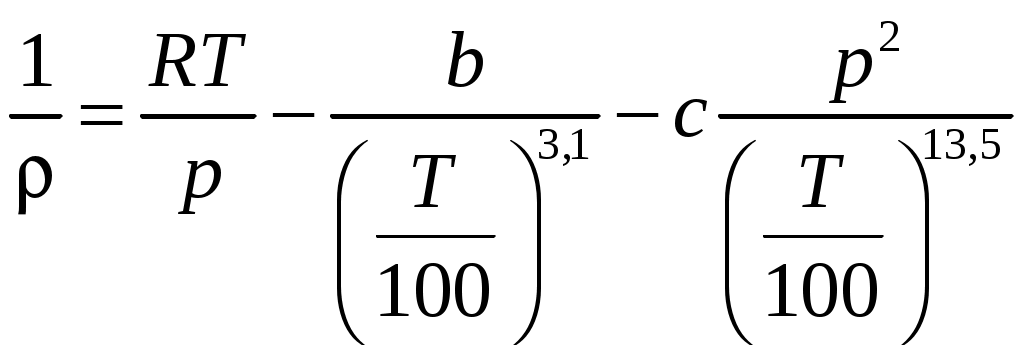
,
где b и с – постоянные. В зависимости от вида уравнения состояния выражения для внутренней энергии газа и его теплосодержания имеют разную форму.

Основные свойства жидкостей и газов
Рассмотрим ряд общих для всех жидкостей и газов механических свойств, которые отличают их от твердых тел.

Механические связи между частицами жидкостей и газов весьма слабы, поэтому их частицы обладают очень большой подвижностью и в связи с этим текучестью – одним из основных свойств жидкостей и газов, о котором уже говорилось. Рассмотрим другие свойства.