Гл. 1. Общие вопросы аэрогазодинамики
 Скачать 1.17 Mb.
|
СжимаемостьЖидкости и газы способны в широких пределах деформироваться, изменяя не только свою форму, но и свой объем. Способность жидкостей и газов изменять свой объем под действием сжимающих усилий называется сжимаемостью. Сжимаемость газов существенно выше, чем у жидкостей. Количественно оценить сжимаемость позволяет коэффициент сжимаемости. Выделим объем 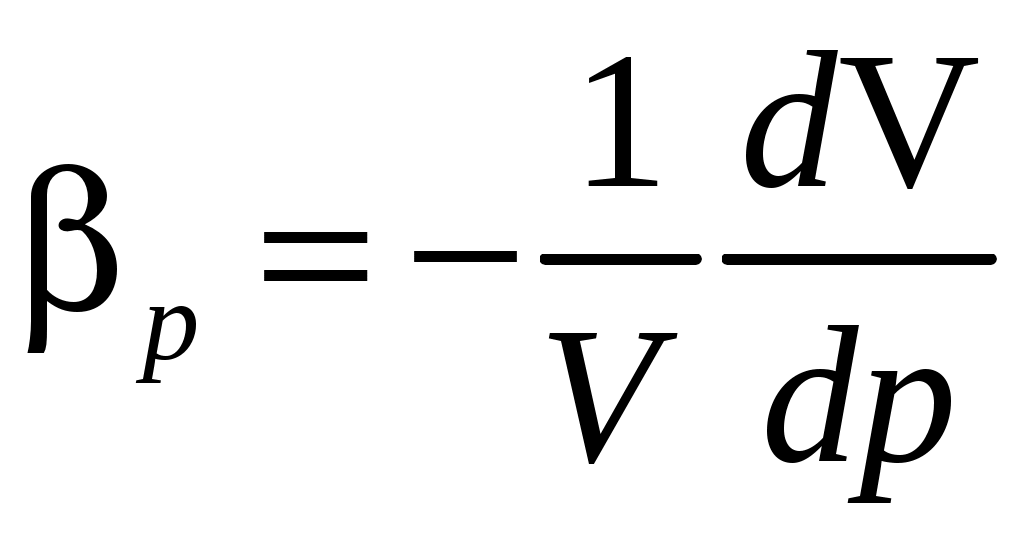 жидкости или газа. Пусть он находится под давлением  . Если изменить величину давления на  , то объем изменится на величину  и относительное изменение объема (объемная относительная деформация) будет равно  . Величину этой деформации, приходящейся на единицу изменения давления, называют коэффициентом сжимаемости:  ,отсюда 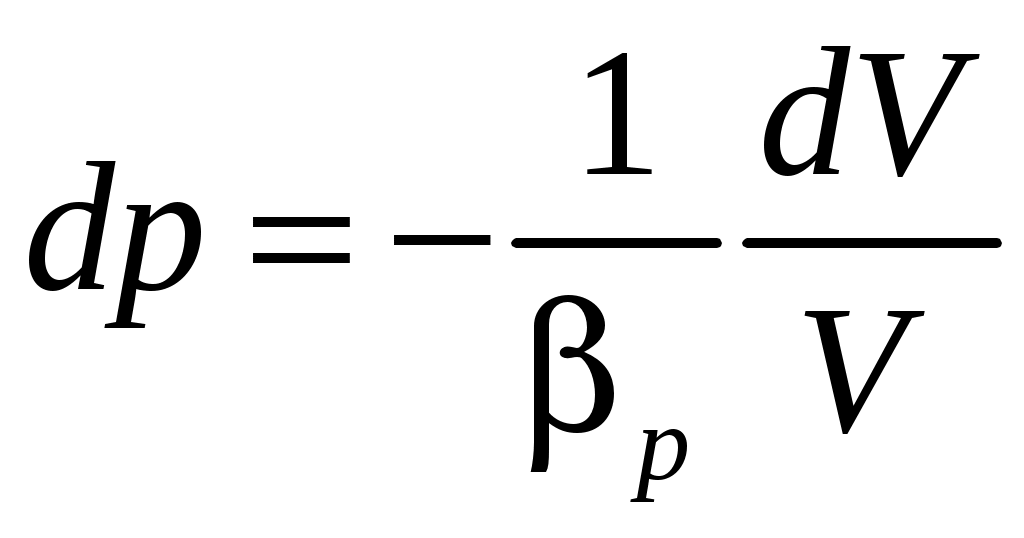 .Знак «минус» показывает, что при сжатии величина объема уменьшается. Из выражения видно, что 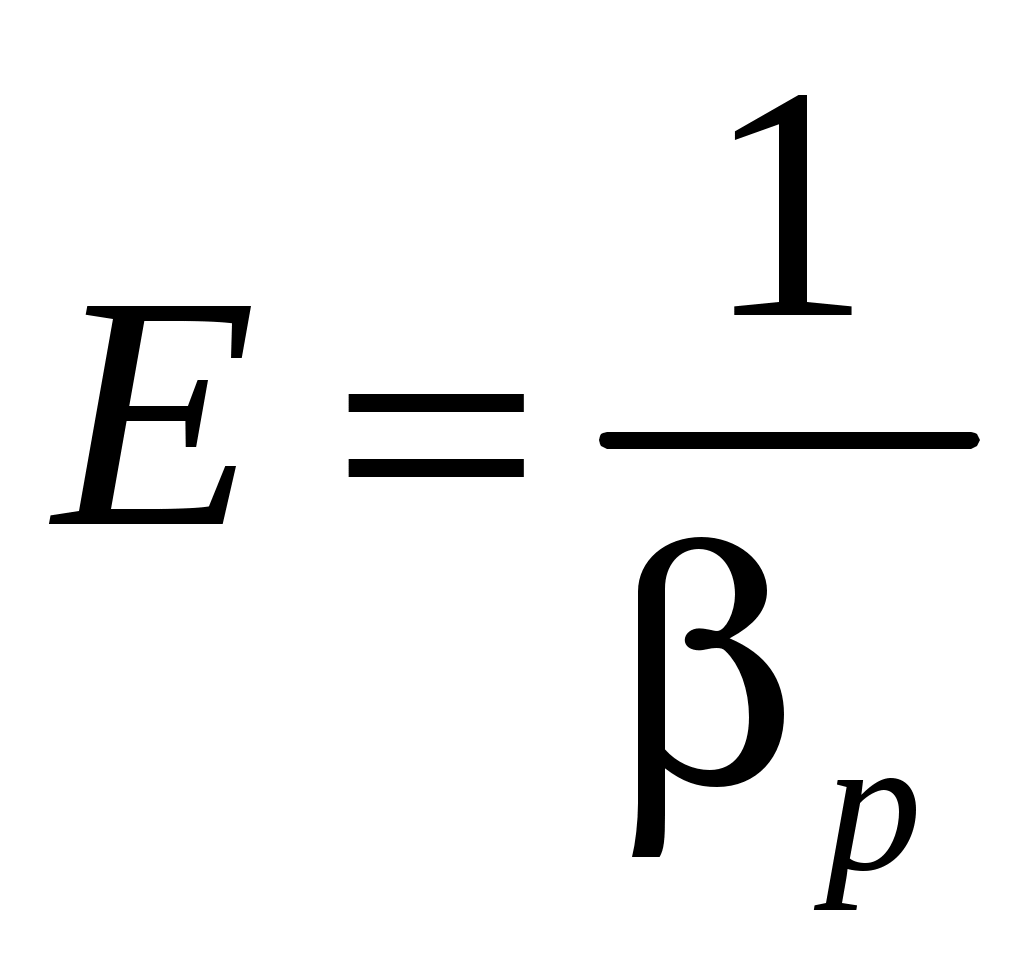 есть объемный модуль упругости  данной жидкости или газа, т. е. коэффициент пропорциональности в законе Гука:  ,тогда  .Коэффициент сжимаемости  для жидкостей и газов не является постоянной величиной:  Для газов  , т. е. модуль упругости пропорционален давлению p.Сжимаемость капельных жидкостей гораздо меньше, чем сжимаемость газов. Так при нормальных условиях для воды она в 13 900 раз ниже, чем для воздуха. Поэтому при решении многих задач механики капельные жидкости можно считать несжимаемыми. Так как законы движения для жидкостей и газов во многом одинаковы, то обычно жидкости и газы объединяют под общим названием «жидкости», различая их по сжимаемости: несжимаемые (капельные жидкости) и сжимаемые (газы). Усилия, которые возникают в жидкостях и газах при сжатии, могут достигать огромных величин. Однако ни жидкость и ни газ не выдерживают сколь-нибудь значительных растягивающих усилий. При растяжении даже малыми усилиями в них возникают пустоты, разрывы. Поэтому будем считать, что при отсутствии разрывов и пустот отсутствуют и растягивающие усилия. Все жидкости изменяют свой объем и при изменении температуры. Изменение объема характеризует коэффициент теплового расширения  , равный объемной относительной деформации, приходящейся на единицу изменения температуры:  .В общем случае  . При малых изменениях температуры можно считать  и  , где  – объем жидкости при температуре  .Наряду с коэффициентом сжимаемости и модулем упругости сжимаемость может быть охарактеризована другими параметрами, с которыми мы ознакомимся ниже. Вязкость Все жидкости и газы обладают в той или иной мере вязкостью. Вязкостью называется способность жидкостей и газов сопротивляться усилиям, касательным к поверхности выделенного объема, т. е. усилиям сдвига. К жидкостям с малой вязкостью относятся вода, воздух и другие газы. Жидкости с большой вязкостью – это глицерин, минеральное масло и др. У капельных жидкостей вязкость – это свойство, обратное текучести. Она представляет собой проявление механических связей между частицами (сил сцепления). Под действием этих связей молекулы колеблются относительно своих средних по времени положений. Так как кинетическая энергия колеблющейся молекулы увеличивается с ростом температуры, то усиливается и ее колебательное движение. Вследствие этого механические связи ослабевают, и вязкость жидкости уменьшается. И наоборот, вязкость жидкости будет резко расти с приближением температуры к точке замерзания. Физическое происхождение вязкости у газов иное. Кинетическая теория учит, что молекулы газов совершают беспорядочное тепловое движение. Молекулы движутся равномерно и прямолинейно до столкновения с другими молекулами. Когда молекулы из какого-либо слоя движущейся жидкости попадают в другой, с иной скоростью движения, то в результате столкновения они обмениваются количествами движения и тем самым изменяют скорость течения газа. Таким образом, диффузия молекул, сопровождаемая переносом количества движения из одного слоя в другой, является причиной возникновения силы, касательной к слоям (силы трения). Как известно из кинетической теории газов, с ростом температуры растет скорость теплового движения молекул, увеличивается перенос количества движения и, следовательно, увеличивается вязкость газов. К  асательные усилия в жидкостях и газах, по сравнению с нормальными к поверхности сжимающими усилиями, обычно весьма малы (иногда меньше почти в тысячу раз). Это позволяет при решении многих задач, связанных с определением нормальных усилий (расчет распределения нагрузок по поверхности ЛА, аэродинамического момента), пренебрегать касательными усилиями и вязкостью, т. е. перейти к идеальной жидкости.Выделим на поверхности  рассматриваемого объема жидкости элементарную площадку  (рис. 1.1). Пусть на нее действует поверхностная сила  (сила, действие которой распределено по поверхности рассматриваемого объема). Тогда напряжение поверхностных сил в данной точке равно .Составляющие поверхностных напряжений следующие: нормальная – аэродинамическое давление p и касательная – напряжение трения . Н 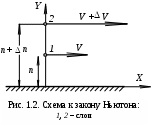 апряжение трения возникает только тогда, когда одни частицы жидкости движутся относительно других или относительно граничных поверхностей.Рассмотрим простейший случай, когда все частицы жидкости движутся параллельно какой-либо плоскости (рис. 1.2). Относительная скорость направленного движения частиц в слое 2 по отношению к слою 1 равна  . Чем больше разность скоростей, тем больше силы трения между слоями. То есть касательное напряжение  , или в пределе при  имеем следующее:  , (1.1)где  – коэффициент пропорциональности, который называют коэффициентом динамической вязкости, Н · с/м2.Выражение (1.1) представляет собой закон Ньютона для касательных напряжений при ламинарном течении. Из кинетической теории газов известно, что  , где  – плотность;  – средняя скорость движения молекул;  – длина свободного пробега молекул, пропорциональная  .С ростом температуры растет и средняя скорость движения молекул, вследствие чего коэффициент динамической вязкости также будет расти. Величина давления (в очень широком диапазоне изменения) практически не влияет на величину . Так увеличение давления приводит к росту плотности газа и одновременному уменьшению длины свободного пробега молекул. То есть влияние давления на величину взаимно компенсируется, и можно считать, что  .Влияние температуры на вязкость капельных жидкостей и газов имеет разный характер (табл. 1.1). Таблица 1.1 Влияние температуры на вязкость
Наряду с коэффициентом динамической вязкости широко используется и другая характеристика вязкости среды – так называемый коэффициент кинематической вязкости  . Свое название этот коэффициент получил потому, что в его размерности фигурируют только кинематические единицы. Коэффициенты вязкости и связаны простым соотношением:  (1.2)Можно сказать, что коэффициент кинематической вязкости характеризует ускорение частиц, вызванное силами вязкости. Из кинетической теории газов следует, что  . Следовательно, на величину оказывают влияние и температура газа, и его давление, т. е.  .Приведем некоторые формулы для расчета коэффициента динамической вязкости: 1. Формула Сатерленда: 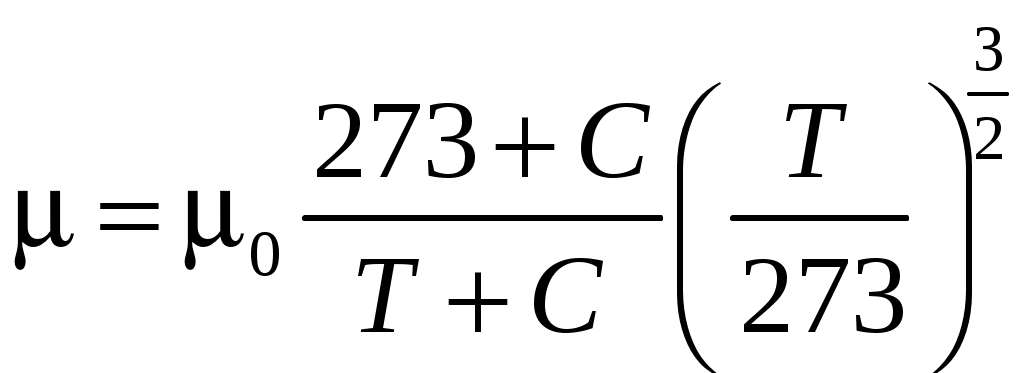 , (1.3)где  – значение коэффициента динамической вязкости при температуре  ,  (Н с / м 2);  – постоянная Сатерленда (для воздуха  ).2. Приближенная формула, которая используется довольно часто: 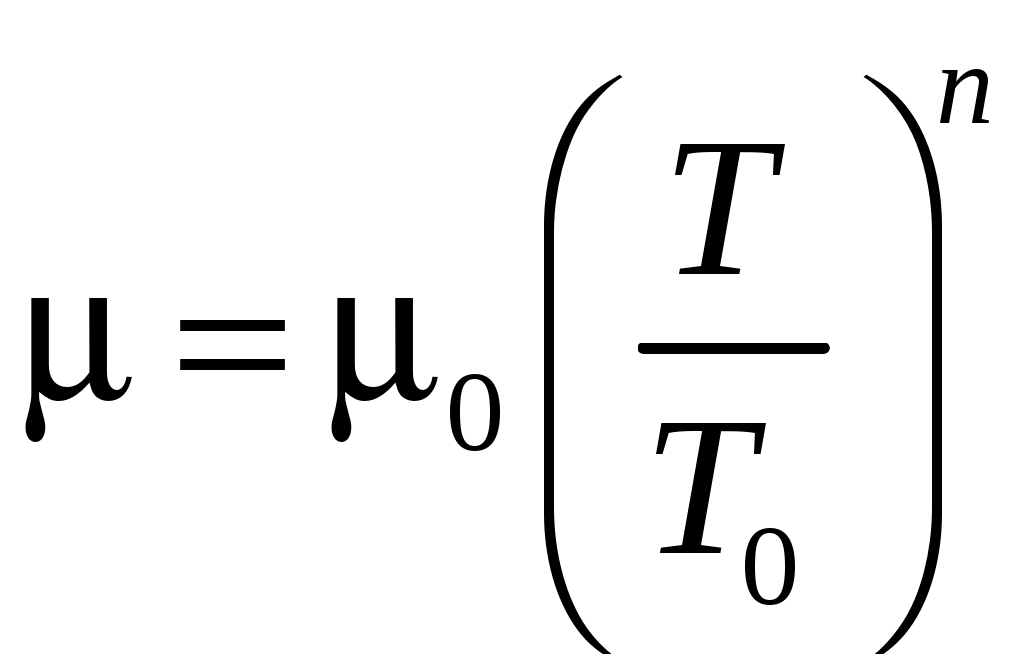 , (1.4)где  при температурах, близких к нормальной (для воздуха при  ).3. Формула Кузнецова  (Н с/м2), в которой температура берется по шкале Цельсия.Теплопроводность Процесс теплопроводности в газе, так же как и происхождение сил вязкости, связан с молекулярным строением газа. Вследствие диффузии молекул между слоями жидкости происходит не только перенос количества движения, но и перенос энергии, т. е. передача тепла за счет теплопроводности. Количество тепла, которое проходит в единицу времени вследствие теплопроводности сквозь единичную площадку соприкосновения двух тел, выражается законом Фурье, вид которого аналогичен закону Ньютона для вязкостного трения (пригоден для ламинарного течения):   (1.5)где  – коэффициент теплопроводности,   – температурный градиент по нормали к площадке.Примечание: знак «минус» в формуле (1.5) связан с разной ориентацией векторов теплового потока и градиента температуры: теплота распространяется в сторону убывающих температур, тогда как производная  положительна в направлении возрастающих температур.Суждения о порядке величины коэффициента теплопроводности для твердых, жидких и газообразных веществ позволяют сделать некоторые выборочные данные, приведенные для комнатной температуры (табл. 1.2). Наихудшими проводниками тепла являются газы, а капельные жидкости имеют на порядок выше. Однако специальные теплоизолирующие материалы имеют достаточно низкую теплопроводность, обусловленную их структурой, включающей в себя свободные объемы, заполненные воздухом. Следует отметить, что величины для газовых смесей приходится находить опытным путем, так как правила аддитивности здесь дают результат с большими ошибками. Таблица 1.2 Коэффициенты теплопроводности некоторых веществ
К  оэффициент , как и , зависит от вида газа и температуры. При увеличении температуры растет. При высоких температурах коэффициент теплопроводности реального газа  .Рассмотрим процесс переноса тепла с точки зрения молекулярно-кинети-ческой теории (рис. 1.3). Количество тепла, переносимое единицей массы, равно  , где U – внутренняя энергия единицы массы газа.Масса молекул, пересекающих при своем движении поверхность с единичной площадью, равна 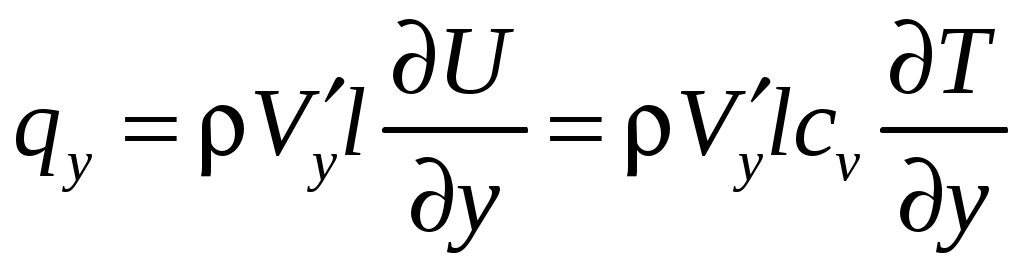 , где  – собстве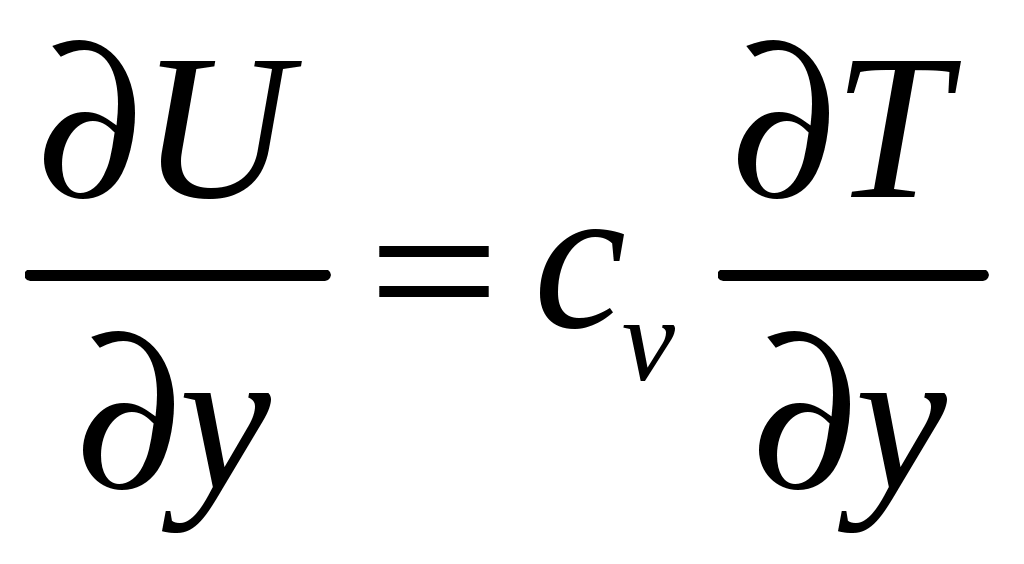нная скорость молекул, т. е. через единичную площадку в единицу времени переносится энергия (количество тепла), равная , (1.6)так как  . Сравнивая формулы (1.5) и (1.6), можно сделать вывод, что  . Таким образом, коэффициент пропорционален скорости хаотического движения молекул, являющейся функцией температуры газа, поэтому  .При температурах до 2 000 К коэффициент теплопроводности можно определить через коэффициент динамической вязкости по следующей формуле: 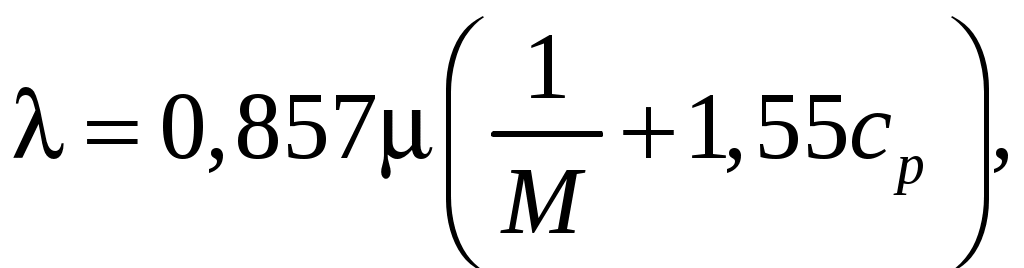 где  – молекулярный вес данного сорта газа.Параметры состояния газа Вспомним объединенный газовый закон 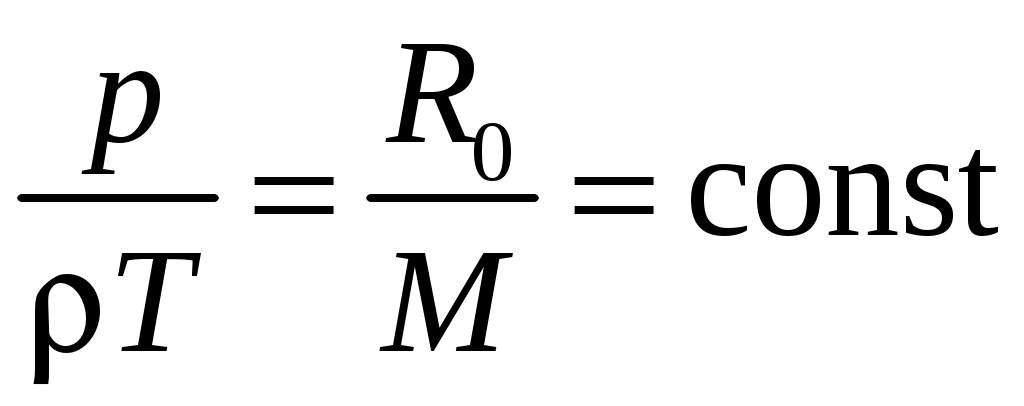 ( ), или уравнение Менделеева–Клапейрона – уравнение состояния идеального газа: или  .Важнейшими характеристиками состояния газа являются давление , плотность и температура  .В общем случае при движении газа эти параметры меняются при переходе от точки к точке и зависят от времени. Для термодинамически совершенного газа , , связаны указанным уравнением Клапейрона. Во многих реальных практических случаях эта связь выражается более сложно. Для реальных газов нельзя пренебрегать собственным объемом молекул и силами взаимодействия между ними. Эти факторы сказываются тем сильнее, чем выше давление.Таким образом, для неустановившегося движения параметры состояния газа являются функциями координат и времени:  ,  ,  Давление. Если скорость движения жидкости V = 0, то касательные напряжения отсутствуют и в жидкости имеются только напряжения сжатия – аэродинамическое давление. Выделим в жидкости бесконечно малый тетраэдр (рис. 1.4), в котором  е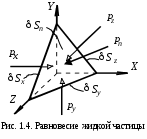сть плоскости граней тетраэдра, перпендикулярных к осям   – давление на этих гранях;  и  – давление и плоскость наклонной грани, взятой произвольно.С  илы, действующие на рассматриваемый объем жидкости, разделяются на поверхностные – силы давления на грани  и объемные – массовая сила  .Так как объем тетраэдра  есть величина третьего порядка малости, а  – второго порядка, то при стягивании тетраэдра в точку массовой силой можно пренебречь.Уравнение равновесия тетраэдра в проекции на ось ОX запишется как  , или  . Поскольку  , то  . Аналогичные результаты получаются для проекций на оси OY и OZ.Следовательно, так как координатные плоскости выбраны произвольно, то  Д 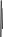 авление в любой точке покоящейся жидкости остается постоянным для всех площадок, проходящих через эту точку, т. е. не зависит от ориентации площадки, на которую оно действует.Единицы измерения давления следующие: в системе СИ 1 Па = 1  ; в технической системе 1 ат =  Па.Плотность. Массовая плотность характеризует распределение массы в среде. Для среды, сплошь заполняющей пространство, плотность есть функция координат точки. Массовая плотность жидкости или газа определяется как  .Для прерывистой среды этот предел мог бы и не существовать. При величине , сравнимой с молекулярными размерами, непрерывное изменение привело бы к прерывистому изменению  . Приняв гипотезу сплошности среды, можно быть уверенным, что предел существует всегда.Единица измерения плотности –  . Например, при нормальных условиях ( ) плотность воды равна  а плотность воздуха  Для газов плотность является функцией давления и температуры,  , а для несжимаемых жидкостей – только температуры,  .Непосредственное измерение плотности движущейся сжимаемой среды затруднено, поэтому 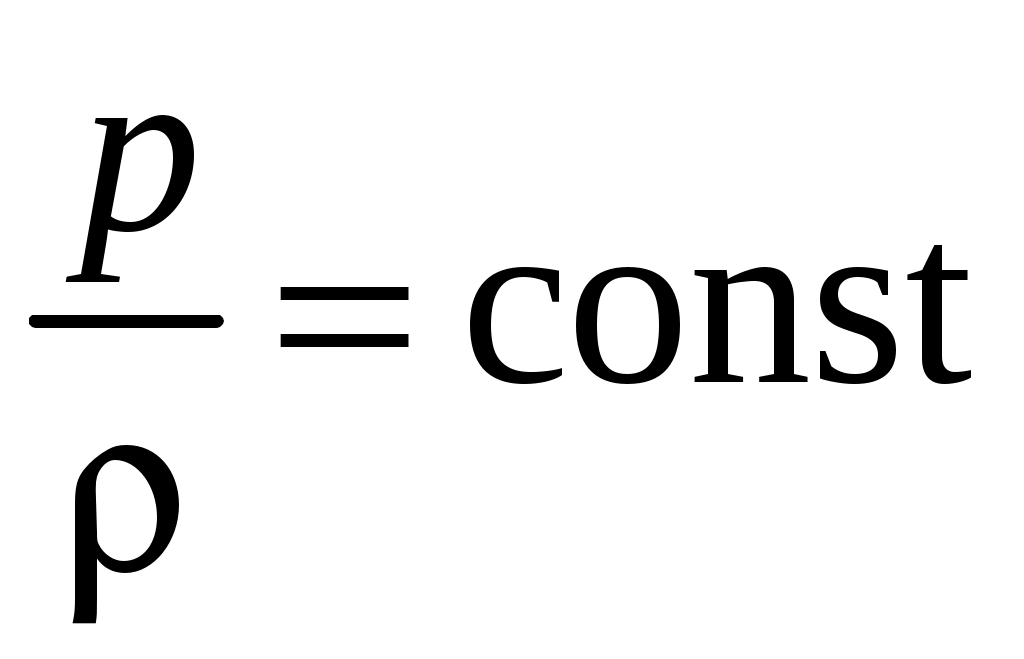обычно определяют косвенным путем. Так для совершенных газов плотность определяют с помощью уравнения Менделеева–Клапейрона, для изотермических процессов ( ) – по уравнению  , для адиабатических процессов – по уравнению 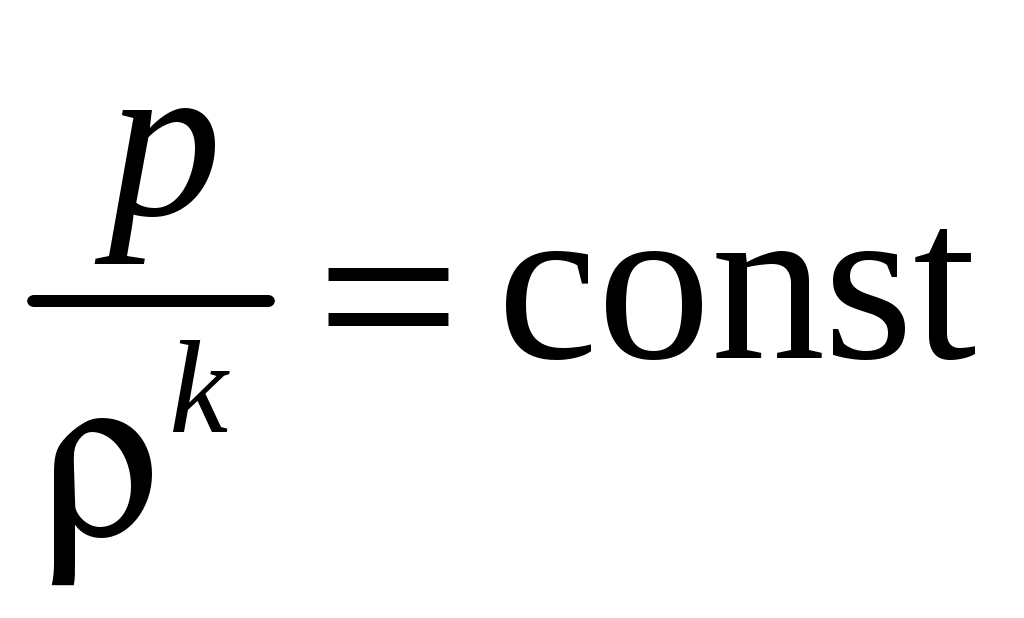 , где  – показатель адиабаты, величина которого зависит от молекулярного строения данного сорта газа; для двухатомных газов k= 1,4. Температура. Температура есть мера внутренней энергии жидкости или газа и вообще любого тела. По величине температуры судят о степени нагретости, т. е. о тепловом состоянии тела. При наличии теплопроводности температура различных частей тела от точки к точке меняется непрерывно. Непрерывность изменения температуры возможна только в сплошных средах. Если же элементарный объем сравним с молекулярными размерами, то | |||||||||||||||||||||||||||||||||||||||||||
, то мы имеем дело с неустановившимся (нестационарным) полем температур, если 
, то поле температур стационарное (установившееся).
, по шкале Кельвина – К (Кельвин). Переход от шкалы Цельсия к шкале Кельвина осуществляется следующим образом: 
. Сила трения определяется с помощью формулы Ньютона. Тогда 
, отсюда 
. Следовательно, 
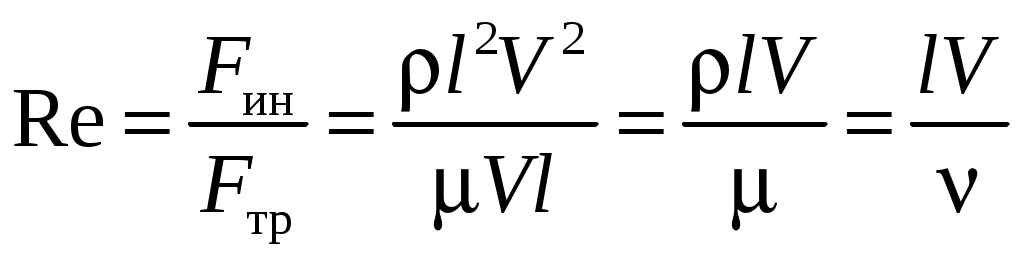. Таким образом,
,
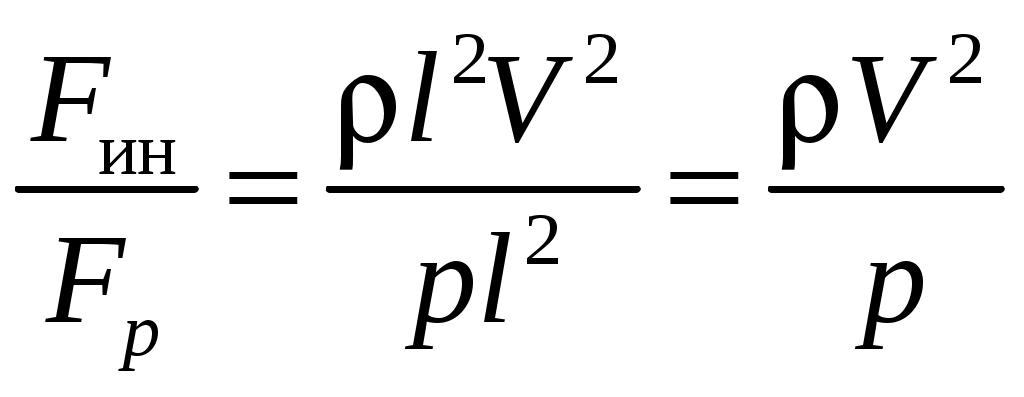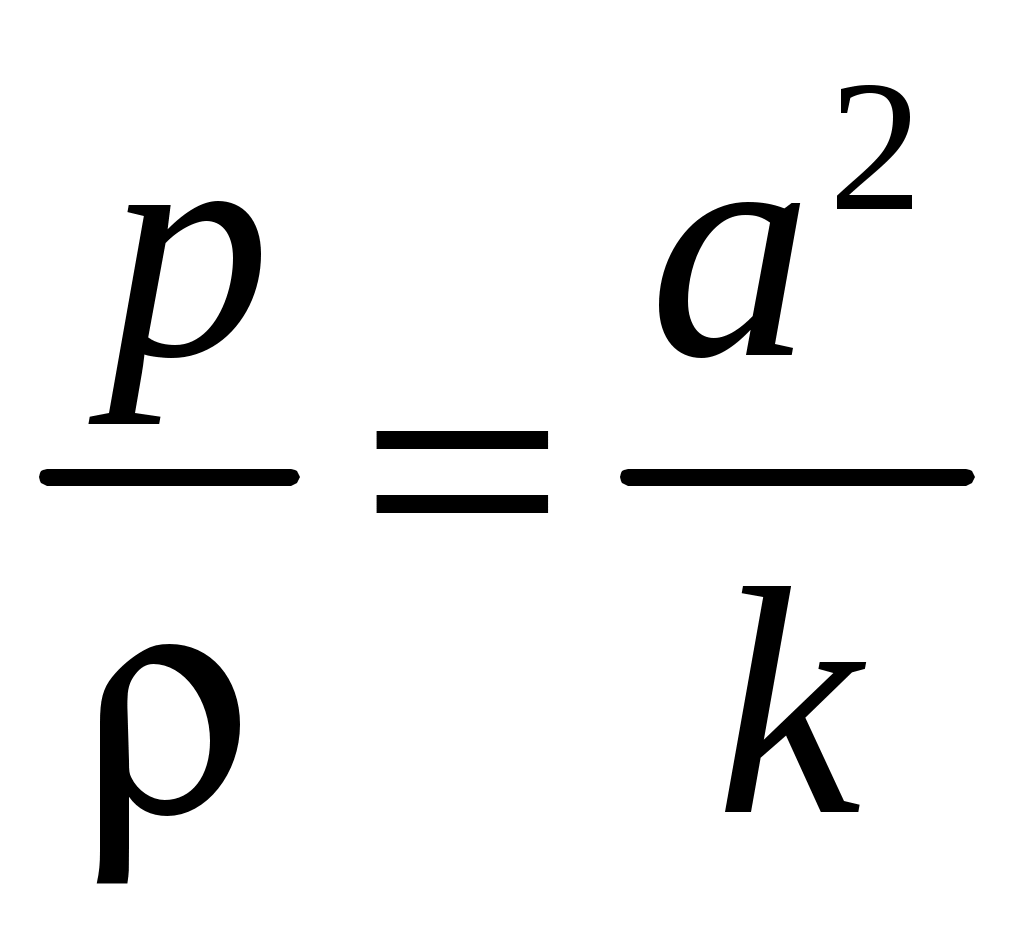мало, силы вязкости преобладают над силами инерции и влияние вязкости имеет существенный характер во всем потоке. Когда число 
.
, то 
, а отношение 
как раз и представляет собой число Маха.