Опорные конспекты по геометрии 8 класс-1. Ок 1 Многоугольники Точки A, B, C, D, е многоугольника
 Скачать 5.42 Mb. Скачать 5.42 Mb.
|
|
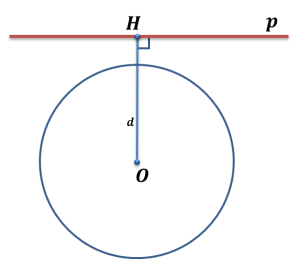
Следствие 2. Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла. 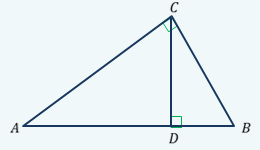 ∆ АВС – прямоуг. ∆ АВС – прямоуг.СD – высота  АC = 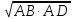 ВC = 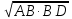 ОК-23 Значения тригонометрических функций для углов 300, 450, 600 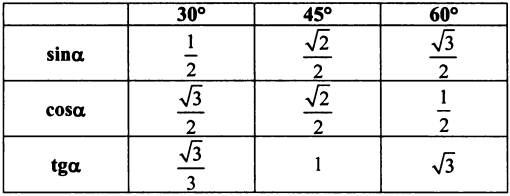 ОК - 24 Взаимное расположение прямой и окружности Общие сведения об окружности   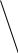  В О – центр окружности (точка, равноудаленная от К всех точек окружности) R = ОА - радиус окружности (отрезок, ОА соединяющий центр окружности с любой ее точкой) М КМ – хорда (отрезок, соединяющий две точки С окружности) d = СВ – диаметр (хорда, проходящая через центр окружности) Свойства окружности: Все радиусы одной окружности равны. Диаметр окружности в два раза больше ее радиуса. Центр окружности является серединой диаметра. Р  адиус равен половине диаметра. адиус равен половине диаметра.d = 2R R= d/2 Взаимное расположение прямой и окружности d – расстояние от прямой до окружности r – радиус окружности
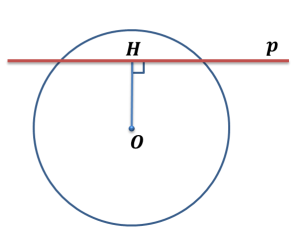
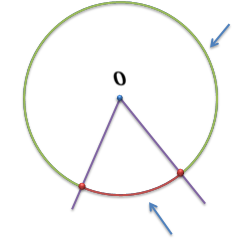
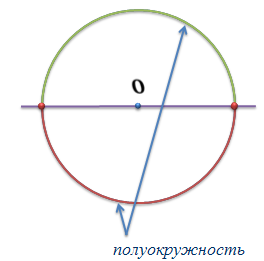
ОК – 25 Касательная к окружности Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. 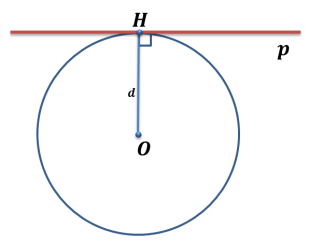 Прямая р – касательная к окружности Прямая р – касательная к окружностиТочка Н – точка касания Свойство касательной к окружности: Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. р – касательная  ОН – радиус, проведенный в точку касания р ┴ ОН ОН – радиус, проведенный в точку касания р ┴ ОНС 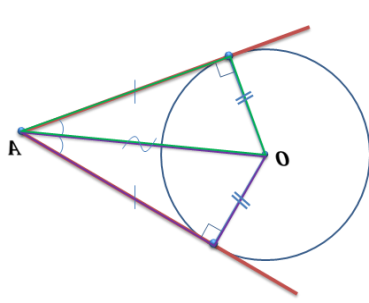 войство отрезков касательных, проведенных из одной точки: Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности. войство отрезков касательных, проведенных из одной точки: Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.С Дано: 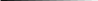 АС, АВ - касательные АС, АВ - касательныеДок-ть: АС = АВ ∠САО =∠ВАО  В ВПризнак касательной: 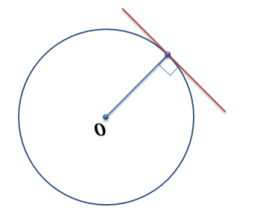 р Если прямая проходит через конец радиуса, р Если прямая проходит через конец радиуса, Н лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.  Н Н 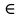 р рр ┴ ОН р – касательная ОК-26 Градусная мера дуги окружности 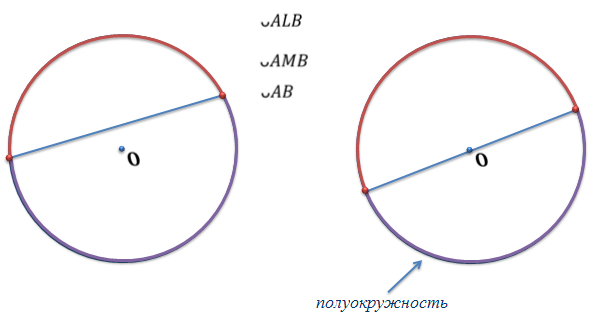 L Дуга– часть окружности. В B А A M Дуга называется полуокружностью, если отрезок, соединяющий ее концы, является диаметром окружности. Центральный угол – угол с вершиной в центре окружности. 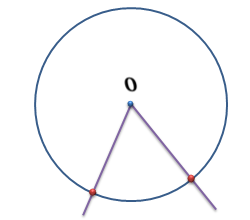 ∠АОВ - центральный 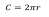 - длина окружности В А 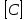 = м, дм, см = м, дм, см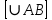 = м, дм, см, 0 = м, дм, см, 0
ОК-28 Свойство биссектрисы угла Т  очка равноудалена от двух прямых точка находится на одинаковом расстоянии от этих прямых. очка равноудалена от двух прямых точка находится на одинаковом расстоянии от этих прямых.   а 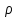 (A;a) = (A;a) =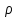 (A; b) (A; b) А ∙ А ∙  b bТеорема. Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.   К В Дано: К В Дано:  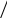 АМ - бис-са ∠ВАС АМ - бис-са ∠ВАС А М М 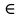 АМ АМДок-ть: L C МК = МL Док-во: проведем МК┴ АВ и МL ┴ АС рассмотрим ∆АКМ и ∆АLМ - прямоуг. ∠  1 = ∠2 ( т.к. АМ - бис-са) ∆АКМ = ∆АLМ 1 = ∠2 ( т.к. АМ - бис-са) ∆АКМ = ∆АLМ  АМ - общая гипотенуза ( по гипотенузе и острому углу) АМ - общая гипотенуза ( по гипотенузе и острому углу) МК = МL МК = МLОбратная теорема. Каждая точка, лежащая внутри угла и равноудаленная от его сторон, лежит на его биссектрисе. Следствия: Геометрическим местом точек плоскости, лежащих внутри неразвернутого угла и равноудаленных от сторон угла, является биссектриса этого угла. Биссектрисы треугольника пересекаются в одной точке. О 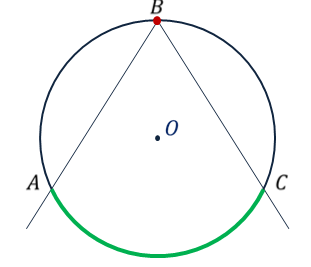 К-27 Вписанный угол К-27 Вписанный угол Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность. ∠АВС – вписанный ∠АВС опирается на 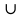 АС АСТеорема. Вписанный угол равен половине дуги, на которую он опирается. Дано: ∠АВС – вписанный Док-ть: ∠АВС = 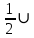 АС АС Док-во: Луч ВО совпадает со стороной ∠АВС 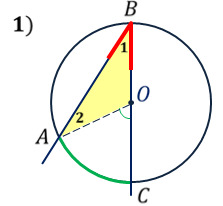 ∠АОС = ∠АОС = 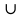 АС АС ∠АОС = ∠1 + ∠2 (как внешний угол ∆АВО) ∆   АВО – равнобедренный(ОА=ОВ=R) ∠1 = ∠2 АВО – равнобедренный(ОА=ОВ=R) ∠1 = ∠2 ∠АОС = 2 ∙ ∠1 ∠АВС = ∠1 = 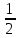 ∠АОС = ∠АОС = 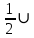 АС АС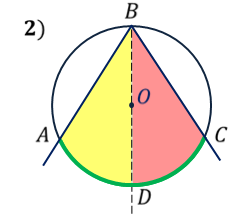 Луч ВО делит ∠АВС на два угла (внутри угла) ∠АВD = 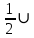 АD АD∠CВD = 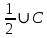 D D∠АВС = ∠АВD + ∠CВD = 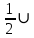 АD + АD + 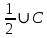 D = = D = = 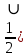 АD + АD + 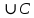 D) = D) = 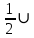 АС АС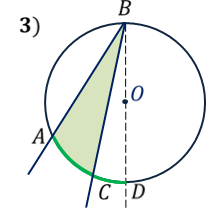 Луч ВО не делит ∠АВС на два угла (вне угла) ∠АВD = 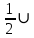 АD АD∠CВD = 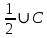 D D∠АВС = ∠АВD – ∠CВD = 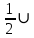 АD – АD – 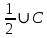 D = = D = = 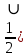 АD – АD – 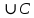 D) = D) = 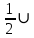 АС АССледствия: Вписанные углы, опирающиеся на одну и ту же дугу, равны.   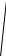   1 ∠1 = 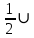 АС АС  2 ∠2 = 2 ∠2 = 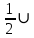 АС ∠1 = ∠2 АС ∠1 = ∠2 А С Вписанный угол, опирающийся на полуокружность – прямой.    1 1 А ∙ С ∠1 = А ∙ С ∠1 = 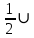 АС АС АС = 180 0 ∠1 = 90 0 АС = 180 0 ∠1 = 90 0 ОК-29 Серединный перпендикуляр Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему. 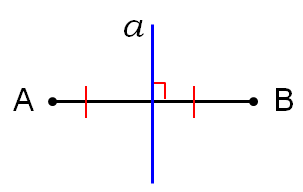 а ┴ АВ  АО = ОВ а - серединный перпендикуляр АО = ОВ а - серединный перпендикуляр О Теорема. Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. 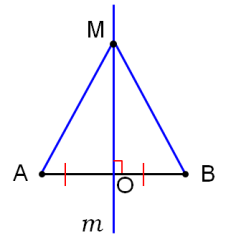 Дано: а - сер. ┴ М  а а Док-ть: АМ = МВ Док-во: а  - сер. ┴ а ┴ АВ и АО = ОВ - сер. ┴ а ┴ АВ и АО = ОВ Рассмотрим ∆ МАО и ∆ МВО - прямоуг.  АО = ОВ ∆ МАО = ∆ МВО АО = ОВ ∆ МАО = ∆ МВО МО - общий катет (по двум катетам) АМ = МВ МО - общий катет (по двум катетам) АМ = МВОбратная теорема. Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему. Следствия: Геометрическим местом точек, равноудаленных от концов отрезка , является серединный перпендикуляр к нему. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. 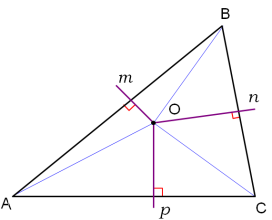 ОК-30 Замечательные точки треугольника Т 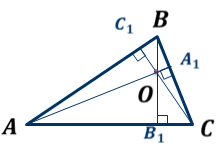 еорема. Высоты треугольника (или их продолжения) пересекаются в одной точке. еорема. Высоты треугольника (или их продолжения) пересекаются в одной точке. ВВ1 ┴ АС  АА1 ┴ ВС ВВ1 АА1 ┴ ВС ВВ1  АА1 АА1 СС1 = О СС1 = ОСС1 ┴ АВ т.О - ортоцентр Ортоцентр - точка пересечения высот треугольника. 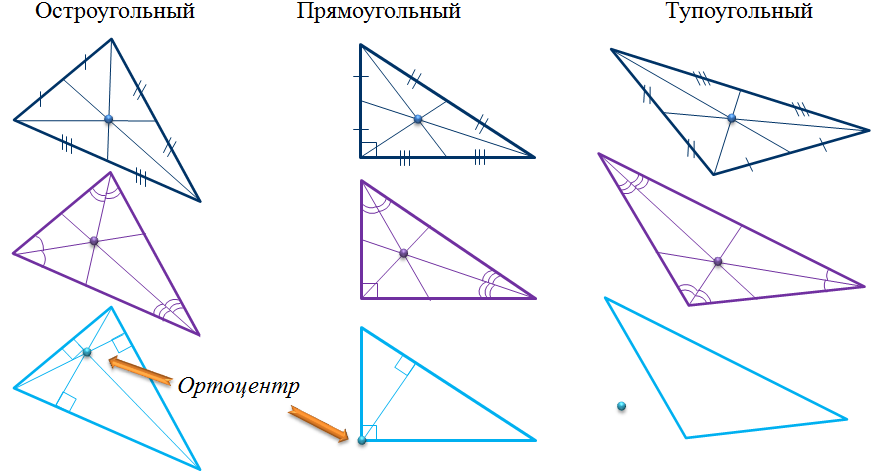 В остроугольном треугольнике ортоцентр - внутри треугольника. В прямоугольном треугольнике ортоцентр - вершина прямого угла. В тупоугольном треугольнике ортоцентр - вне треугольника. Замечательные точки треугольника: точка пересечения медиан точка пересечения биссектрис 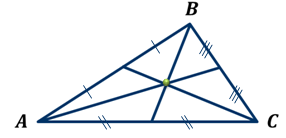 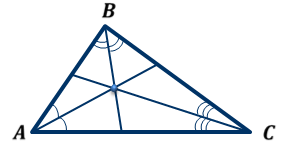 точка пересечения точка пересечения высот 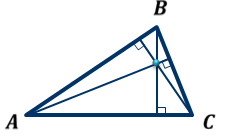 серединных перпендикуляров серединных перпендикуляров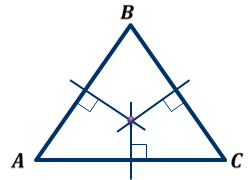 |