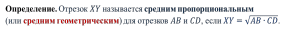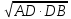|
|
Опорные конспекты по геометрии 8 класс-1. Ок 1 Многоугольники Точки A, B, C, D, е многоугольника
Египетский
треугольник
О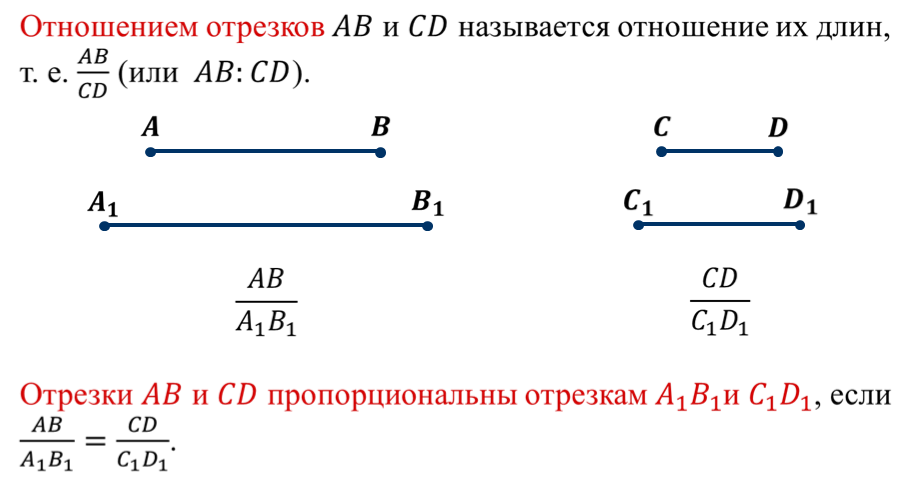 К-17 Пропорциональные отрезки. Подобные треугольники К-17 Пропорциональные отрезки. Подобные треугольники
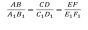 Т Т ри отрезка АВ, CD и EF пропорциональны трем отрезкам А1В1, С1D1 и E1F1, если справедливо равенство: ри отрезка АВ, CD и EF пропорциональны трем отрезкам А1В1, С1D1 и E1F1, если справедливо равенство:
Фигуры одинаковой формы называют подобными.
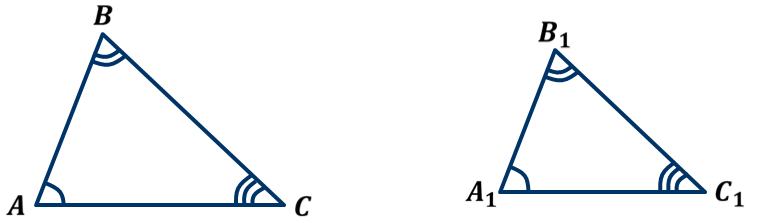
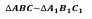
∠ А=∠А1, ∠ А=∠А1, ∠ В=∠В1, ∠ В=∠В1, ∠ С=∠С1 С=∠С1
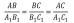
(стр. 138) 2)
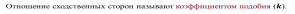
Коэффициент подобия показывает, во сколько раз стороны одного треугольника больше сторон другого треугольника.
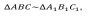 Теорема. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. Теорема. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
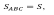 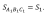  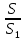 = k2 (к - коэффициент подобия) = k2 (к - коэффициент подобия)
ОК-18 Первый признак подобия треугольников
1-й признак подобия треугольников. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
    А Дано: А Дано:
А1 ∆ АВС, ∆ А1В1С1
∠А=∠А1, ∠В=∠В1
В С В1 С1 Док-ть: ∆ АВС ∆ А1В1С1 ∆ А1В1С1
Док-во:
∠С =180 о – (∠А + ∠В)
 ∠С1 =180 о – (∠А1 + ∠В1) ∠С=∠С1 ∠С1 =180 о – (∠А1 + ∠В1) ∠С=∠С1
∠А=∠А1, ∠В=∠В1
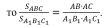
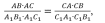
Т.к. ∠А=∠А1 , (1) (1) = (2)
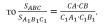
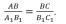
Т.к. ∠С=∠С1 , (2)
(3)
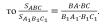
Т.к. ∠В=∠В1, (4)
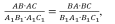 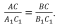
= (4) (5) (4) (5)
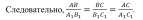
(3) = (5)
∠А=∠А1, ∠В=∠В1, ∠С=∠С1
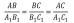  ∆ АВС ∆ АВС ∆ А1В1С1 ∆ А1В1С1
Следствия :
Прямая, параллельная одной из сторон треугольника, отсекает от него треугольник, подобный данному.
 M M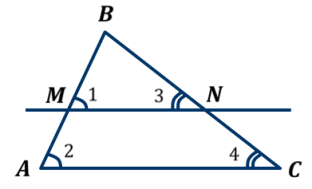 N║AC ∆ MNB N║AC ∆ MNB  ∆ АСВ ∆ АСВ
Прямоугольные треугольники подобны по острому углу.
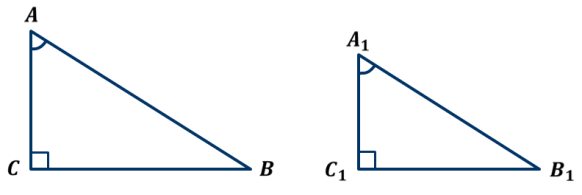
∆ АВС и ∆ А1В1С1 – прямоуг. ∆ АВС АВС и ∆ А1В1С1 – прямоуг. ∆ АВС ∆ А1В1С1 ∆ А1В1С1
∠А=∠А1
ОК – 19 Второй и третий признаки подобия треугольников
2-й признак подобия треугольников. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между ними равны, то такие треугольники подобны.
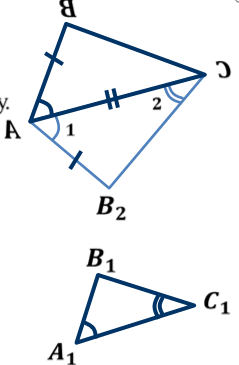
Дано:
∆ АВС, ∆ А1В1С1
∠А=∠А1
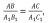
Док-ть: ∆ АВС ∆ А1В1С1 ∆ А1В1С1
Док-во:
Рассмотрим АВ2С : ∠1=∠А1, ∠2=∠С1
∠ 1=∠А1, ∠2=∠С1 ∆ АВ2С 1=∠А1, ∠2=∠С1 ∆ АВ2С ∆ А1В1С1 ∆ А1В1С1
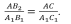
( по 1 признаку)
(т.к. ∆ АВ2С ∆ А1В1С1) ∆ А1В1С1)
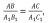 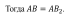
(по условию)
АВ = АВ2
А С – общая ∆ АВ2С С – общая ∆ АВ2С = ∆ АВС ( по 1 признаку) = ∆ АВС ( по 1 признаку)
∠1=∠А1=∠А
∆ АВ2С ∆ А1В1С1 ∆ А1В1С1
 ∆ АВ2С ∆ АВ2С = ∆ АВС ∆ АВС = ∆ АВС ∆ АВС ∆ А1В1С1 ∆ А1В1С1
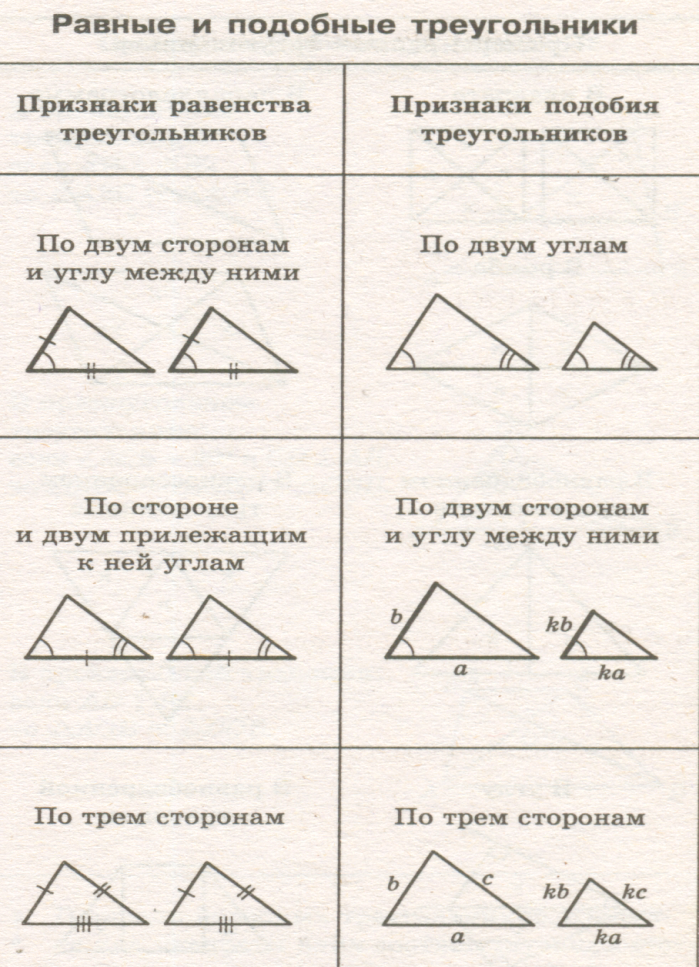
3-й признак подобия треугольников. Если три стороны одного треугольника соответственно пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.
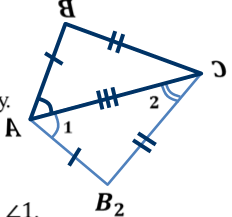
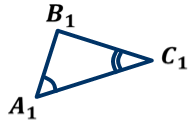 Дано: Дано:
∆ АВС, ∆ А1В1С1
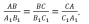
Док-ть: ∆ АВС ∆ А1В1С1 ∆ А1В1С1
Док-во:
Рассмотрим АВ2С : ∠1=∠А1, ∠2=∠С1
∠ 1=∠А1, ∠2=∠С1 ∆ АВ2С 1=∠А1, ∠2=∠С1 ∆ АВ2С ∆ А1В1С1 (по 1 признаку) ∆ А1В1С1 (по 1 признаку)
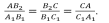
∆ АВ2С АВ2С ∆ А1В1С1 ∆ А1В1С1
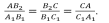
(т.к. ∆ АВ2С ∆ А1В1С1) ∆ А1В1С1)
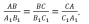
АВ = АВ2 и
(по условию) ВС = В2С
АВ = АВ2
 ВС = В2С ∆ АВ2С ВС = В2С ∆ АВ2С = ∆ АВС ( по 3 признаку) = ∆ АВС ( по 3 признаку)
АС – общая
∆ АВ2С ∆ А1В1С1 ∆ А1В1С1
 ∆ АВ2С ∆ АВ2С = ∆ АВС ∆ АВС = ∆ АВС ∆ АВС ∆ А1В1С1 ∆ А1В1С1
ОК-20 Средняя линия треугольника
Средняя линия треугольника – отрезок, соединяющий середины двух его сторон.
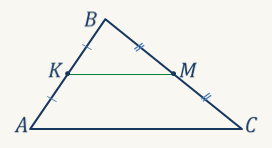  К – середина АВ (АК=КВ) КМ – средняя К – середина АВ (АК=КВ) КМ – средняя
М – середина ВС (ВМ=МС) линия
Теорема (свойство средней линии треугольника):
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
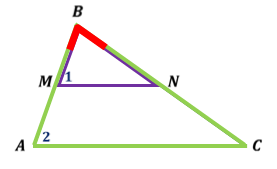 Дано: Дано:
 МN – ср. линия ∆ АВС МN – ср. линия ∆ АВС
Док-ть:
MN ║ АС
MN = 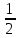 АС АС
Док-во:
М   – середина АВ ВM = – середина АВ ВM = 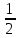 АВ АВ 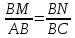 = =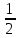
 N – середина ВC ВN = N – середина ВC ВN = 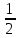 ВC ВC
∠B – общий
 ∆ АВС ∆ АВС
∆ МВN (по 1 пр.)
∆  АВС АВС
∆ МВN ∠1=∠2 MN ║ АС
∠1 и ∠2 – соотв. при АС и MN и сек. АВ
∆  АВС АВС
∆ МВN к = 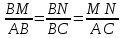 = =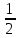 MN = MN = 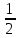 АС АС

М N – ср. линия ∆ АВС MN ║ АС и MN = N – ср. линия ∆ АВС MN ║ АС и MN = 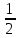 АС АС
Свойство медиан треугольника:
Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины.
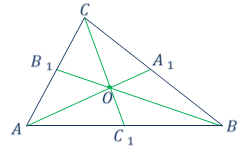
АА1, ВВ1, СС1 - медианы
ОК -22 Синус, косинус, тангенс острого угла
прямоугольного треугольника
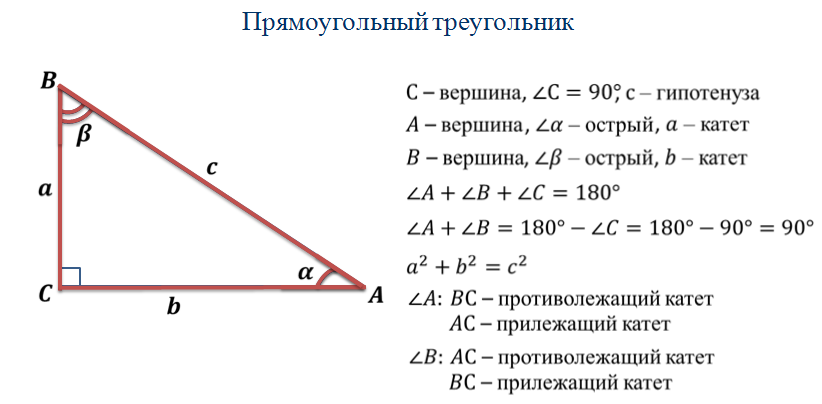

sin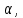 cos cos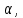 tg tg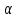 - тригонометрические функции - тригонометрические функции
Определение: синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
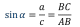 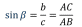
Определение: косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
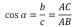 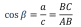
Определение: тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
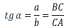 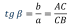
 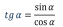 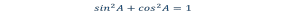
основное тригонометрическое
тождество
Теорема. Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.
ОК-21 Пропорциональные отрезки в прямоугольном треугольнике
Задача. Докажите, что высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
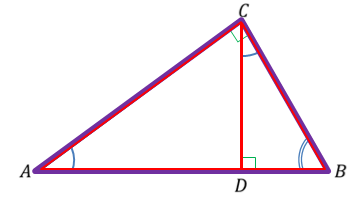 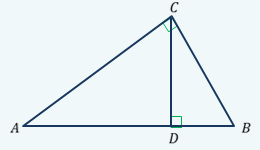 Дано: Дано:
∆ АВС – прямоуг.
СD – высота
 Док-ть: Док-ть:
∆ АСD
∆ СDВ
∆ АСD ∆ АВС
∆ СDВ ∆ АВС
Док-во:
∆ АСD и ∆ СDВ – прямоуг. → ∠D = 900
∠В = 900 - ∠А →
∠ВСD = 900 - ∠В = 900 - (900 - ∠А) = 900 - 900 + ∠А =∠А
→ ∆ АСD ∆ СDВ ( по 1 пр.)
∆ АСD – прямоуг. → ∠D = 900
∆ АВС– прямоуг. → ∠С = 900
∠D = ∠С = 900
∠А – общий → ∆ АСD ∆ АВС ( по 1 пр.)
∆ СDВ – прямоуг. → ∠D = 900
∆ АВС– прямоуг. → ∠С = 900
∠D = ∠С = 900
∠В – общий → ∆ СDВ ∆ АВС ( по 1 пр.)
Следствие 1.
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.
 ∆ АВС – прямоуг. ∆ АВС – прямоуг.
СD – высота

CD = 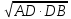
|
|
|
 Скачать 5.42 Mb.
Скачать 5.42 Mb. А=∠А1, ∠
А=∠А1, ∠ В=∠В1, ∠
В=∠В1, ∠ С=∠С1
С=∠С1  (4) (5)
(4) (5) 1=∠А1, ∠2=∠С1 ∆ АВ2С
1=∠А1, ∠2=∠С1 ∆ АВ2С ∆ А1В1С1
∆ А1В1С1 ∆ А1В1С1)
∆ А1В1С1)  ∆ А1В1С1
∆ А1В1С1 1=∠А1, ∠2=∠С1 ∆ АВ2С
1=∠А1, ∠2=∠С1 ∆ АВ2С ∆ А1В1С1 (по 1 признаку)
∆ А1В1С1 (по 1 признаку) АВ2С
АВ2С ∆ А1В1С1
∆ А1В1С1 ∆ А1В1С1)
∆ А1В1С1) ∆ А1В1С1
∆ А1В1С1 АС
АС 

 – середина АВ ВM =
– середина АВ ВM = 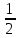 АВ
АВ 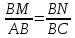 =
=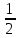

 АВС
АВС 
 АВС
АВС 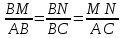 =
=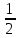 MN =
MN = 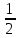 АС
АС 
 N – ср. линия ∆ АВС MN ║ АС и MN =
N – ср. линия ∆ АВС MN ║ АС и MN = 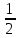 АС
АС 
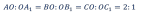


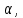 cos
cos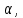 tg
tg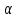 - тригонометрические функции
- тригонометрические функции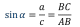
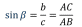
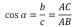
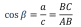
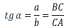
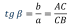

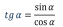
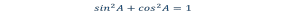

 Дано:
Дано:  Док-ть:
Док-ть: 
 К-17 Пропорциональные отрезки. Подобные треугольники
К-17 Пропорциональные отрезки. Подобные треугольники 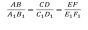
 ри отрезка АВ,
ри отрезка АВ, 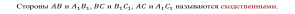

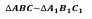
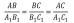
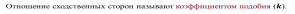
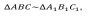
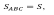
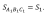
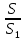 = k2 (к - коэффициент подобия)
= k2 (к - коэффициент подобия)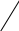

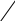
 А Дано:
А Дано:
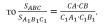
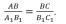
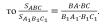
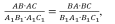
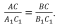
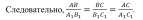
 N║AC ∆ MNB
N║AC ∆ MNB 

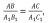
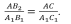
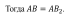
 = ∆ АВС ( по 1 признаку)
= ∆ АВС ( по 1 признаку)
 Дано:
Дано: 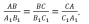
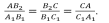


 Дано:
Дано: МN – ср. линия ∆ АВС
МN – ср. линия ∆ АВС