Опорные конспекты по геометрии 8 класс-1. Ок 1 Многоугольники Точки A, B, C, D, е многоугольника
 Скачать 5.42 Mb. Скачать 5.42 Mb.
|
|
ОК-9 Осевая и центральная симметрия Осевая симметрия – симметрия относительно прямой. Центральная симметрия – симметрия относительно точки. Задание 1. Построить треугольник, симметричный данному относительно данной прямой. Задание 2. Построить отрезок, симметричный данному относительно данной точки. Задание 3. Ответить письменно на вопросы 18-22 (стр. 114 учебника) ОК -10 Площадь многоугольника Площадь многоугольника – это величина части плоскости, которую занимает многоугольник. 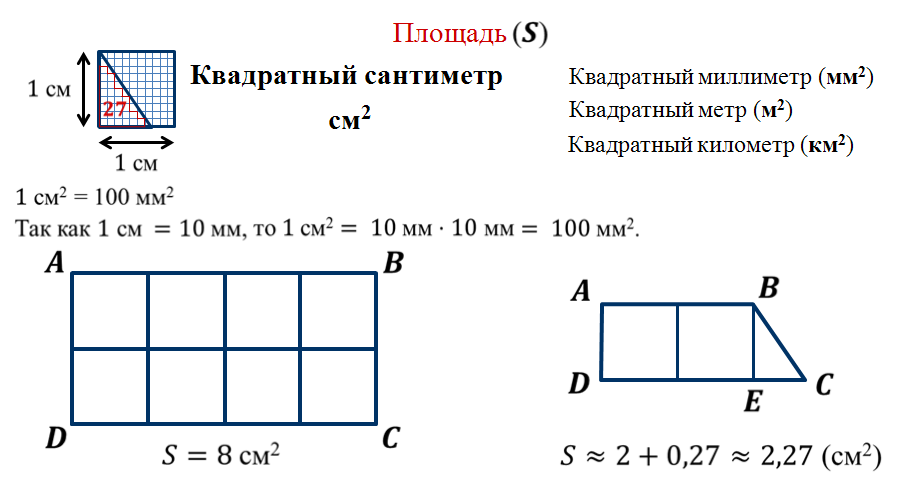 Свойства площадей: Равные многоугольники имеют равные площади. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников. 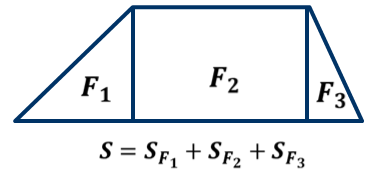 Площадь – величина положительная. Площадь квадрата равна квадрату его стороны. 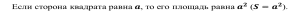 ОК-11 Площадь прямоугольника. Площадь параллелограмма П  лощадь прямоугольника равна произведению его смежных сторон. лощадь прямоугольника равна произведению его смежных сторон. А В А В SABCD = ab a C D b Основание - одна из сторон параллелограмма. В 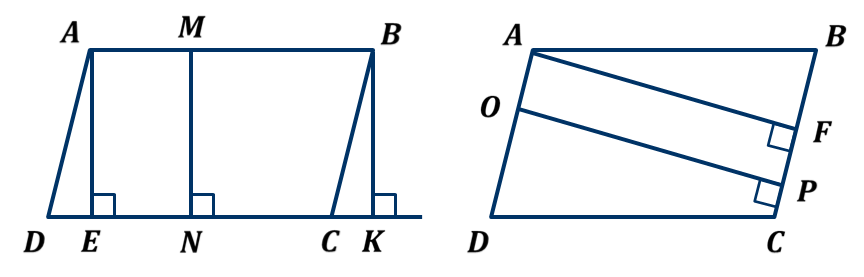 ысотой параллелограмма, проведённой к стороне, называется перпендикуляр, проведённый из любой точки противолежащей стороны к прямой, содержащей основание. ысотой параллелограмма, проведённой к стороне, называется перпендикуляр, проведённый из любой точки противолежащей стороны к прямой, содержащей основание.CD – основание ВС – основание AE, MN, BK– высоты OP, AF – высоты Теорема. Площадь параллелограмма равна произведению его основания на высоту. 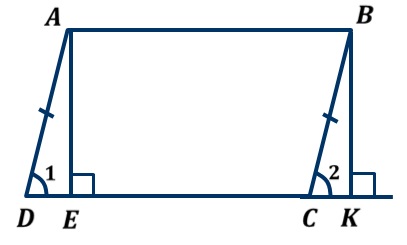 Дано: 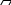 ABCD – ABCD – CD – основание АЕ – высота Док-ть: SABCD = CD∙AE Док-во: Рассмотрим прямоугольные ∆ADE и ∆BCK:  AD =ВС(противоп. стор. парал-ма) ∆ADE = ∆BCK AD =ВС(противоп. стор. парал-ма) ∆ADE = ∆BCK∠1=∠2 (соответсв. при AD║ВС и сек.DC) (по гипот. и остр. углу) ∆  ADE = ∆BCK SADE = SBCK ADE = ∆BCK SADE = SBCKABKD – трапеция SABKD = SABCD + SBCK S  ABKD = SABKE + SADE SABCD = SABKE ABKD = SABKE + SADE SABCD = SABKESADE = SBCK A  BKE – прямоугольник SABKE = АВ∙АЕ BKE – прямоугольник SABKE = АВ∙АЕSABCD = SABKE = АВ∙АЕ А  В = CD SABCD = CD∙AE В = CD SABCD = CD∙AE ОК-13 Площадь трапеции Высотой трапеции называется перпендикуляр, проведённый из любой точки одного из оснований на другое основание или его продолжение.  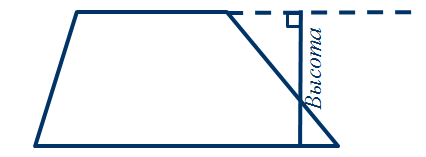 Теорема. Площадь трапеции равна произведению полусуммы длин её оснований на высоту. 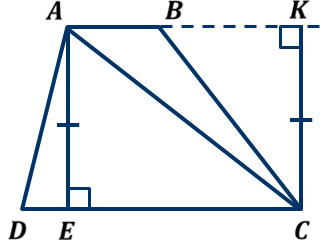 Дано: Дано:АВСD – трапеция АВ, СD – основания АЕ – высота Док-ть: S ABCD = 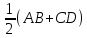 ∙ AE ∙ AEДок-во: Проведем диагональ АС S ABCD = S ABC + S ACD S ACD = 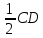 ∙ AE ∙ AEПроведем СК - высоту ∆АВС  S ABC = S ABC = 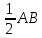 ∙ СК ∙ СК СК = АЕ S ABC = СК = АЕ S ABC = 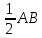 ∙ АЕ ∙ АЕS ABCD = S ABC + S ACD S ABCD = 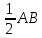 ∙ АЕ + ∙ АЕ + 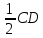 ∙ AE ∙ AES ABCD = 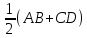 ∙ AE ∙ AE Площадь трапеции равна произведению полусуммы длин её оснований на высоту. 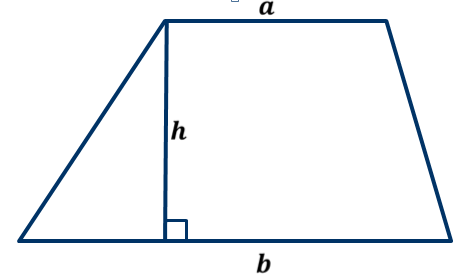 ОК-12 Площадь треугольника Высотой треугольника называется перпендикуляр, проведённый из вершины треугольника на противоположную сторону или её продолжение. Одну из сторон треугольника называют основанием. Под словом «высота» подразумевают высоту треугольника, проведенную к основанию. 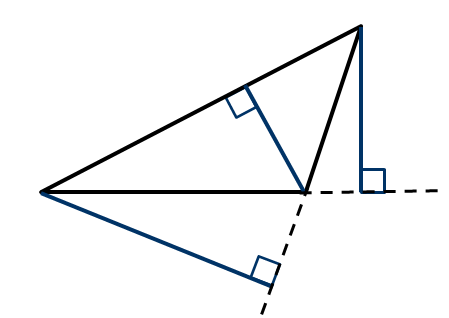 Основание - ВС, высота – АК Основание – АС, высота - ВЕ Основание – АВ, высота - СF Теорема 1. Площадь треугольника равна половине произведения его основания на высоту. 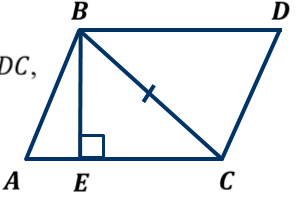 Дано: Дано: ∆ АВС АС – основание ВЕ – высота Док-ть: SАВС =  АС∙ВЕ АС∙ВЕДок-во: Достроим ∆ АВС до параллелограмма АВDC (СD║АВ, BD║АС) СD=АВ (противопол. стор. #)  BD=АС (противопол. стор. #) ∆ АВС=∆ DВС BD=АС (противопол. стор. #) ∆ АВС=∆ DВСВС – общая (по III признаку) ∆  АВС=∆ DВС SАВС = S DВС АВС=∆ DВС SАВС = S DВСSАВDС = SАВС + S DВС = 2 SАВС SАВС = 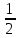 SАВDС SАВDС SАВDС = АС∙ВЕ SАВС = SАВDС = АС∙ВЕ SАВС = 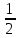 АС∙ВЕ АС∙ВЕ Следствия: П 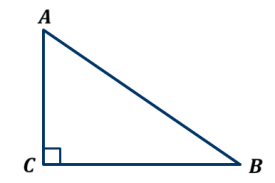 лощадь прямоугольного треугольника равна половине произведения длин его катетов. лощадь прямоугольного треугольника равна половине произведения длин его катетов.SАВС = 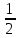 АС∙ВС АС∙ВСЕсли высота одного треугольника равна высоте другого треугольника, то их площади относятся как основания. 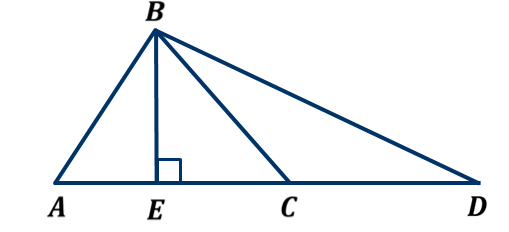 ∆ АВС: АС – основание, ВЕ – высота ∆ АВС: АС – основание, ВЕ – высота∆ CВD: CD – основание, ВЕ – высота SАВС = 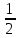 АС∙ВЕ; SCВD = АС∙ВЕ; SCВD = 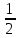 CD∙ВЕ CD∙ВЕ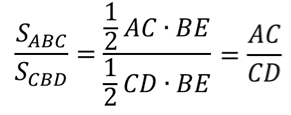 Теорема 2. Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы. 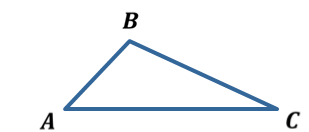 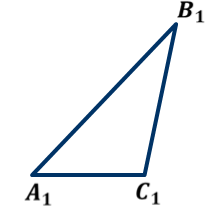 S S1 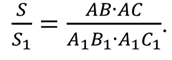 ∆ АВС ∆ АВС ∆ А1В1С1 ∆ А1В1С1 ∠А1=∠А2 ОК-14 Площади
ОК-15 Теорема Пифагора Теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. 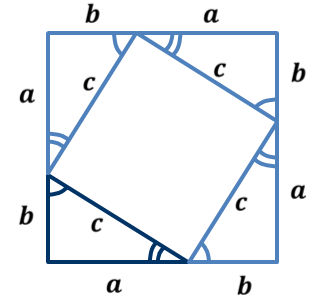 Д  ано: ано: ∆  АВС – прямоуг. АВС – прямоуг.а, b - катеты ac с – гипотенуза Док-ть: b c2 = a2 + b2 Док-во: Достроим треугольник до квадрата со стороной (a+b), как на рисунке. Sкв = (a+b)2 С другой стороны Sкв = 4 Sтр + Sкв1 Sтр = 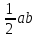 , Sкв1 = с2 , Sкв1 = с2Sкв = 4 ∙ 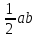 + с2 + с2 4 ∙ 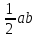 + с2 = (a+b)2 + с2 = (a+b)2 2 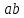 + с2 = a2 +2аb + b2 + с2 = a2 +2аb + b2с2 = a2 +2аb + b2 – 2 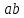 c2 = a2 + b2 Алгоритм решения задач с применением теоремы Пифагора: Указать прямоугольный треугольник; Записать для него теорему Пифагора; Подставить известные значения сторон; Найти неизвестную сторону, произведя вычисления или решив уравнение. Примеры задач. № 1. № 2.   5 ? ? 20 12 16 ОК-16 Теорема, обратная теореме Пифагора Теорема. Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то этот треугольник – прямоугольный. 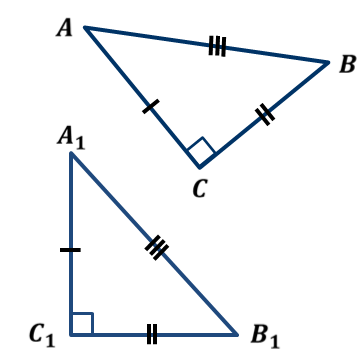 Дано: ∆ АВС АВ2 = АС2 + ВС2 Док-ть: ∆ АВС – прямоугольный Док-во: Рассмотрим ∆ А1В1С1 – прямоугольный такой, что: ∠С1 - прямой А1С1 = АС В1С1 = ВС По теореме Пифагора в ∆ А1В1С1 – прямоуг. А1 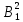 = А1 = А1 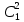 + В1 + В1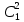  А1С1 = АС А1 А1С1 = АС А1 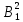 = АС2 + ВС2 = АС2 + ВС2  В1С1 = ВС В1С1 = ВС А   1 1 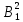 = АС2 + ВС2 = АС2 + ВС2 АВ2 = АС2 + ВС2 А1 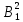 = АВ2 А1В1 = АВ = АВ2 А1В1 = АВА1С1 = АС   В1С1 = ВС ∆ АВС = ∆ А1В1С1 (по III признаку) В1С1 = ВС ∆ АВС = ∆ А1В1С1 (по III признаку)  А1В1 = АВ ∠С = ∠С1 = 900 ∆ АВС – прямоугольный А1В1 = АВ ∠С = ∠С1 = 900 ∆ АВС – прямоугольныйПрямоугольные треугольники, у которых длины сторон выражаются целыми числами, называются пифагоровыми треугольниками.  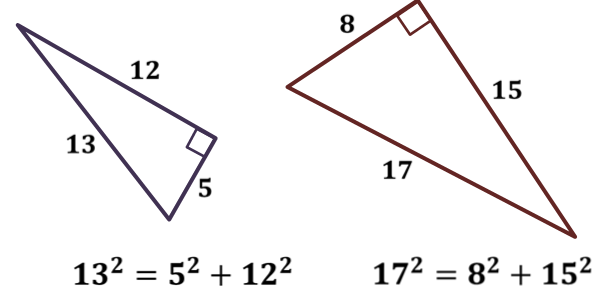 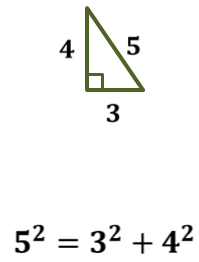 |






 d2
d2