Опорные конспекты по геометрии 8 класс-1. Ок 1 Многоугольники Точки A, B, C, D, е многоугольника
 Скачать 5.42 Mb. Скачать 5.42 Mb.
|
|
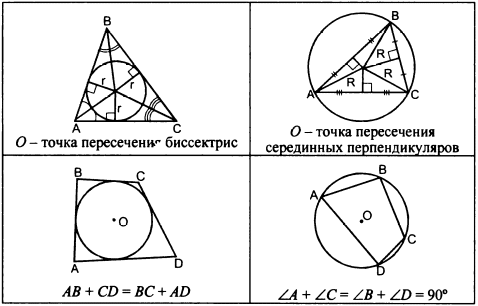
ОК-31 Вписанная окружность Определение. Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности. 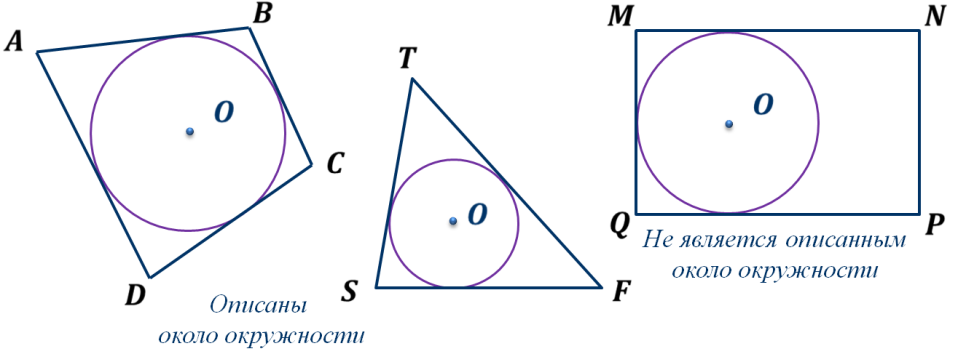 Теорема 1. В любой треугольник можно вписать окружность. 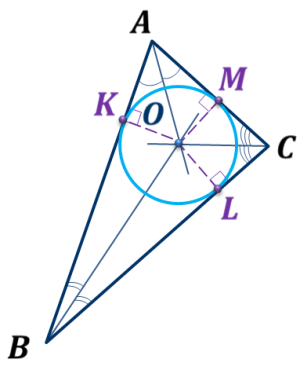 Док-во:   ОК┴АВ, ОМ┴АС, ОL┴ВС ОК=ОМ=ОL ОК┴АВ, ОМ┴АС, ОL┴ВС ОК=ОМ=ОL  К, М, L К, М, L  окр(О; R=ОК) окр(О; R=ОК) А    В┴ ОК, АС┴ОМ, ВС┴ ОL стороны ∆ АВС касаются окр. в точках К, М, L В┴ ОК, АС┴ОМ, ВС┴ ОL стороны ∆ АВС касаются окр. в точках К, М, L окр. вписана в ∆ АВС. Замечания: 1. В треугольник можно вписать только одну окружность. 2. Не во всякий четырехугольник можно вписать окружность. Теорема 2. В любом описанном четырехугольнике суммы противоположных сторон равны. 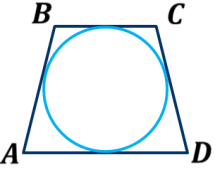 AB + CD = ВC + AD AB + CD = ВC + ADОбратная теорема. Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность. ОК-32 Описанная окружность Определение. Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность. 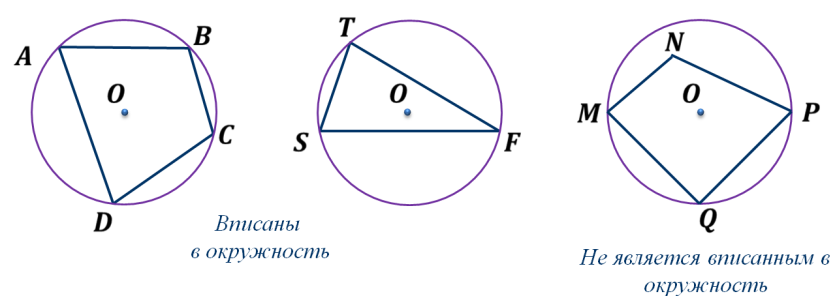 Теорема. Около любого треугольника можно описать окружность.  Замечания: Около любого треугольника можно описать только одну окружность. В отличие от треугольника около четырехугольника не всегда можно описать окружность. В  любом вписанном четырехугольнике сумма противоположных углов равна 1800. любом вписанном четырехугольнике сумма противоположных углов равна 1800. Если сумма противоположных углов четырехугольника равна 1800, то около него можно описать окружность. ОК-33 Окружность (обобщающие сведения)  Свойство хорд окружности 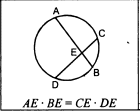  
 ОК-34 Обобщение темы "Четырехугольники"  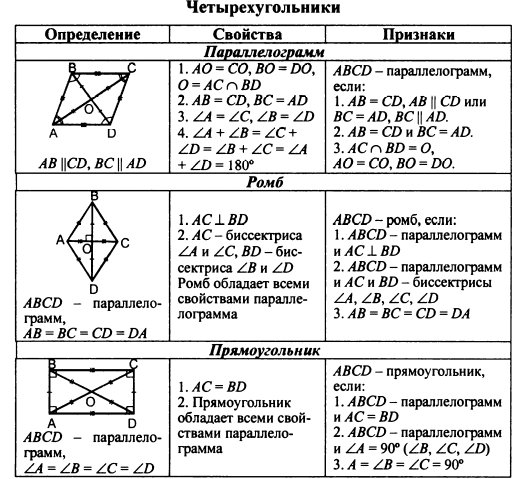  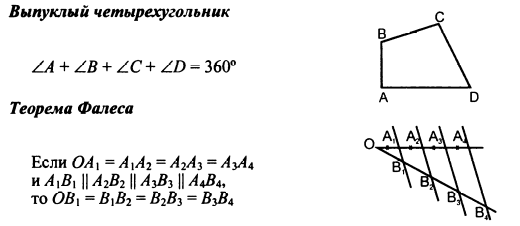 ОК-35 Обобщение темы "Площади фигур"  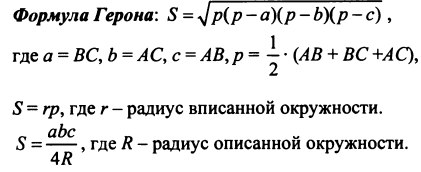 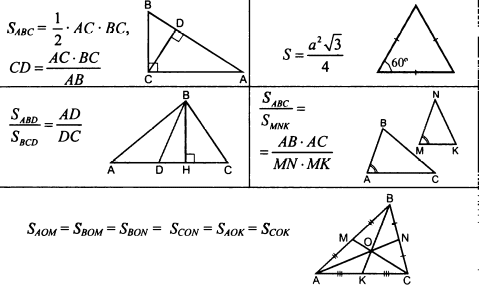 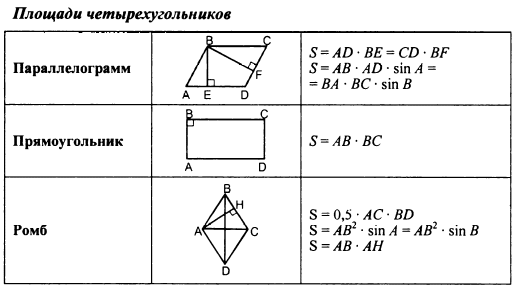 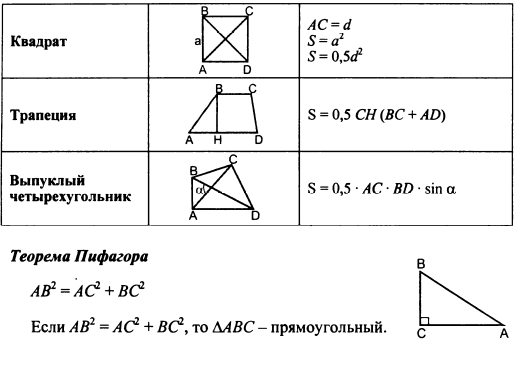 ОПОРНЫЕ КОНСПЕКТЫ ПО ГЕОМЕТРИИ 8  КЛАСС КЛАССМБОУ "Покровская СОШ" учитель математики и физики Александрова Т.В.  |

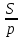 (S- площадь ∆, p - полупериметр)
(S- площадь ∆, p - полупериметр)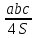 (a,b,c - стороны ∆, S-площадь)
(a,b,c - стороны ∆, S-площадь)