Лекции по математике- часть 6. Операции над матрицами 3 Определители матриц 7

• Название: Операции над матрицами 3 Определители матриц 7
• Анкор: Лекции по математике- часть 6.doc
• Дата: 28.01.2017
• Размер: 1.01 Mb.
• Имя файла: Лекции по математике- часть 6.doc
• Тип: Документы; #716
• страница: 6 из 8

Системы линейных уравнений

Система m линейных уравнений с n переменными в общем виде записывается следующим образом: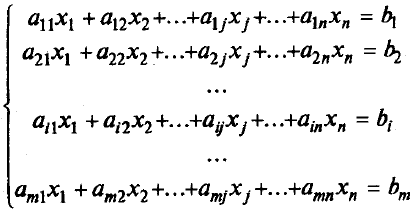



где x_j – переменные, a_ij, b_i – константы, .

При этом величины a_ij (те константы, которые умножаются на переменные) принято называть коэффициентами при переменных, а правые части уравнений b_i (те константы, которые не умножаются на переменные) - свободными членами.

Более кратко ту же систему можно записать в виде: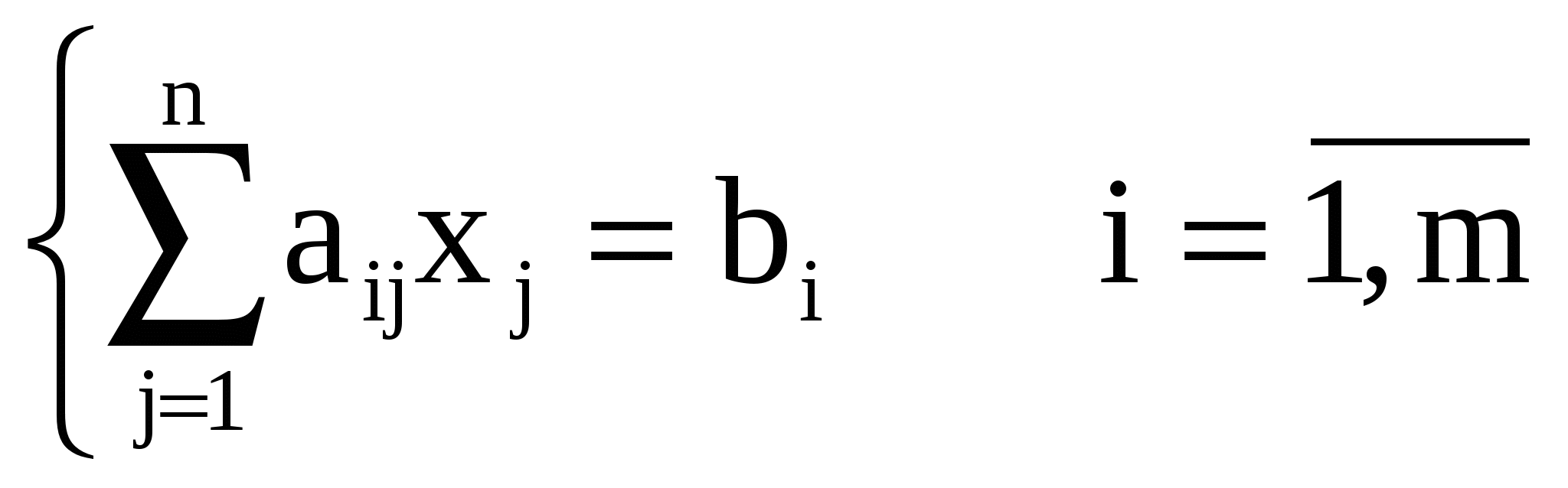



Отметим, что в последней записи тоже записана именно система уравнений, хотя на первый взгляд создается впечатление, что уравнение только одно (запись означает, что такие уравнения записываются m раз для разных i).
Решением такой системы называют совокупность n числовых значений переменных x_j, при подстановке которых в систему каждое уравнение обращается в истинное равенство.

Систему уравнений называют совместной, если она имеет хотя бы одно решение (т.е. хотя бы один такой набор из n чисел), и несовместной, если она не имеет решений.

Совместную систему уравнений называют определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Например, рассмотрим систему уравнений .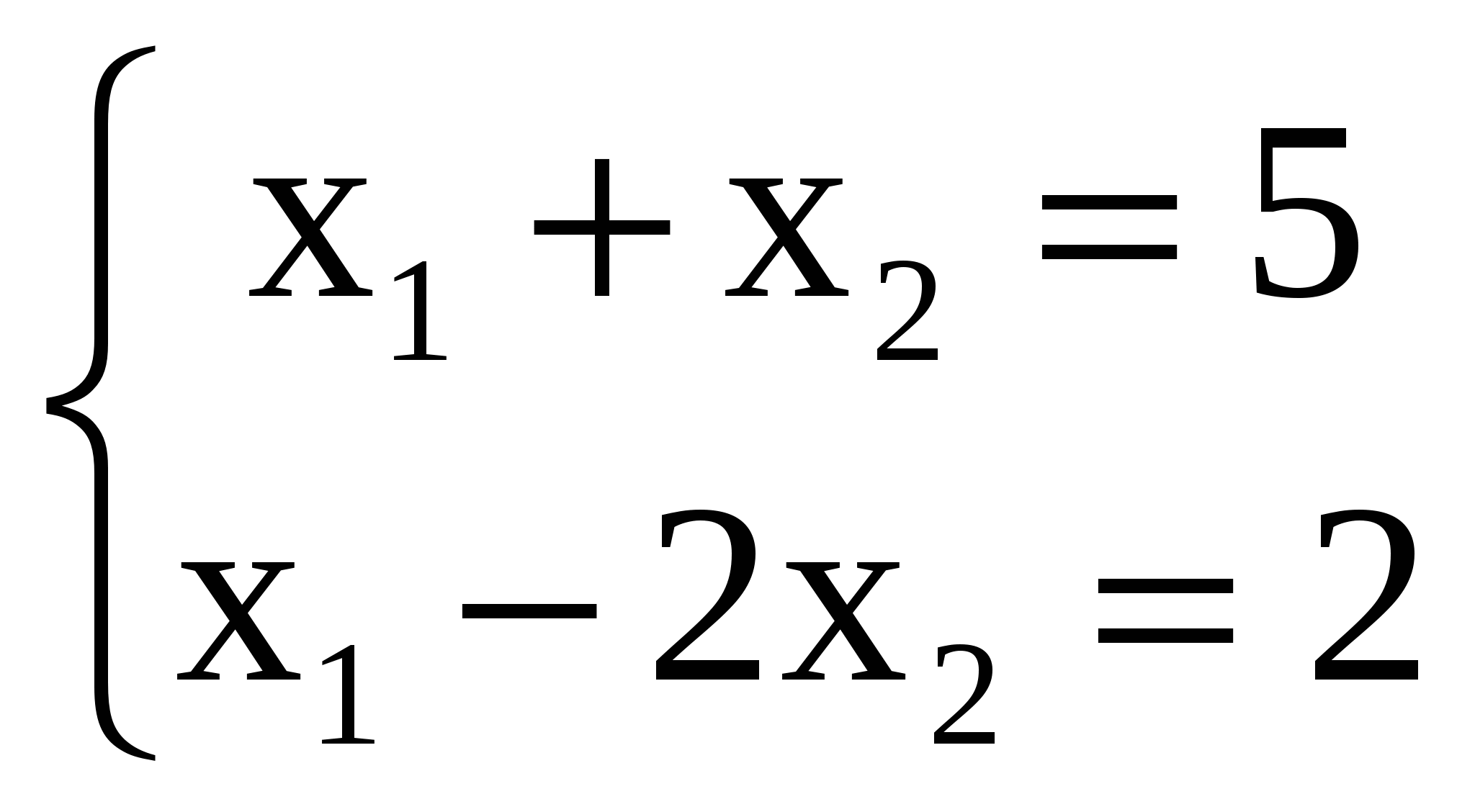

Чтобы решить эту систему, вычтем из верхнего уравнения нижнее. Получим 3х₂ = 3. Отсюда х₂ = 1; и из любого уравнения х₁ = 4. Таким образом, эта система имеет только одно решение – (4; 1). Это означает, что она - совместная и определенная.

Рассмотрим другую систему: 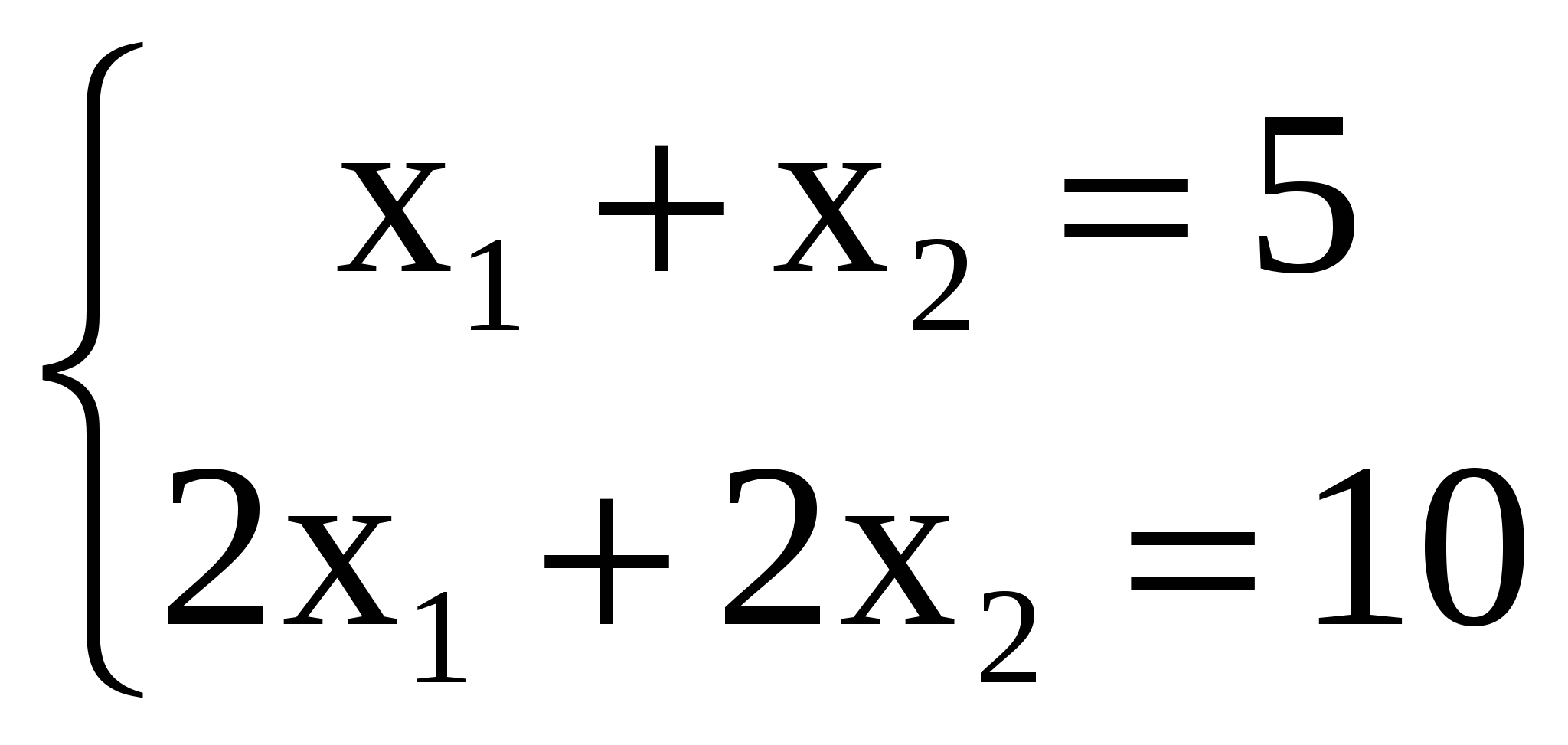. Легко убедиться, что значения (4; 1) будут решением и этой системы тоже. Значит, она тоже совместная. Однако, у нее есть и другие решения, например (2; 3). Значит, она неопределенная. Более того, у этой системы бесконечно много решений. На самом деле, решением здесь будут любые два числа, которые в сумме дают пять, потому что в левой части второго уравнения стоит удвоенная левая часть первого уравнения (если в левой части первого уравнения получено число 5, то во втором всегда будет 10, и оно тоже будет истинным равенством). Таким образом, решение этой системы в общем виде можно записать как ( с; 5 – с), где с – любое число.

Приведем пример несовместной системы: 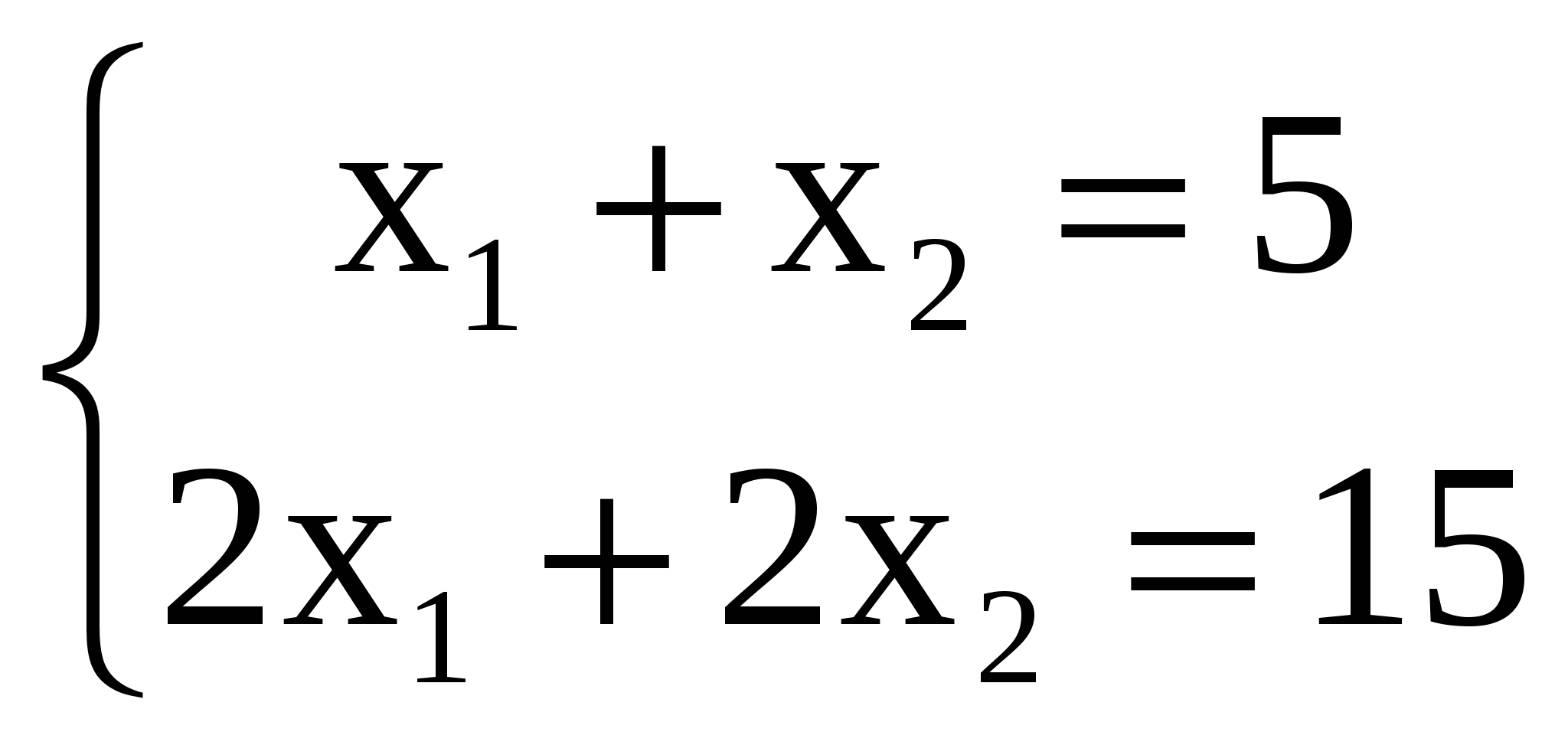. У этой системы, очевидно, нет решений, так как если сумма переменных равна 5, то эта же удвоенная сумма не может равняться 15.
Две системы уравнений называются равносильными, или эквивалентными, если они имеют одно и то же множество решений.
Запишем систему линейных уравнений в общем виде в матричной форме. Обозначим:




Кроме того, для решения систем линейных уравнений используют также понятие расширенной матрицы системы, которую получают, приписав к матрице системы справа столбец свободных членов: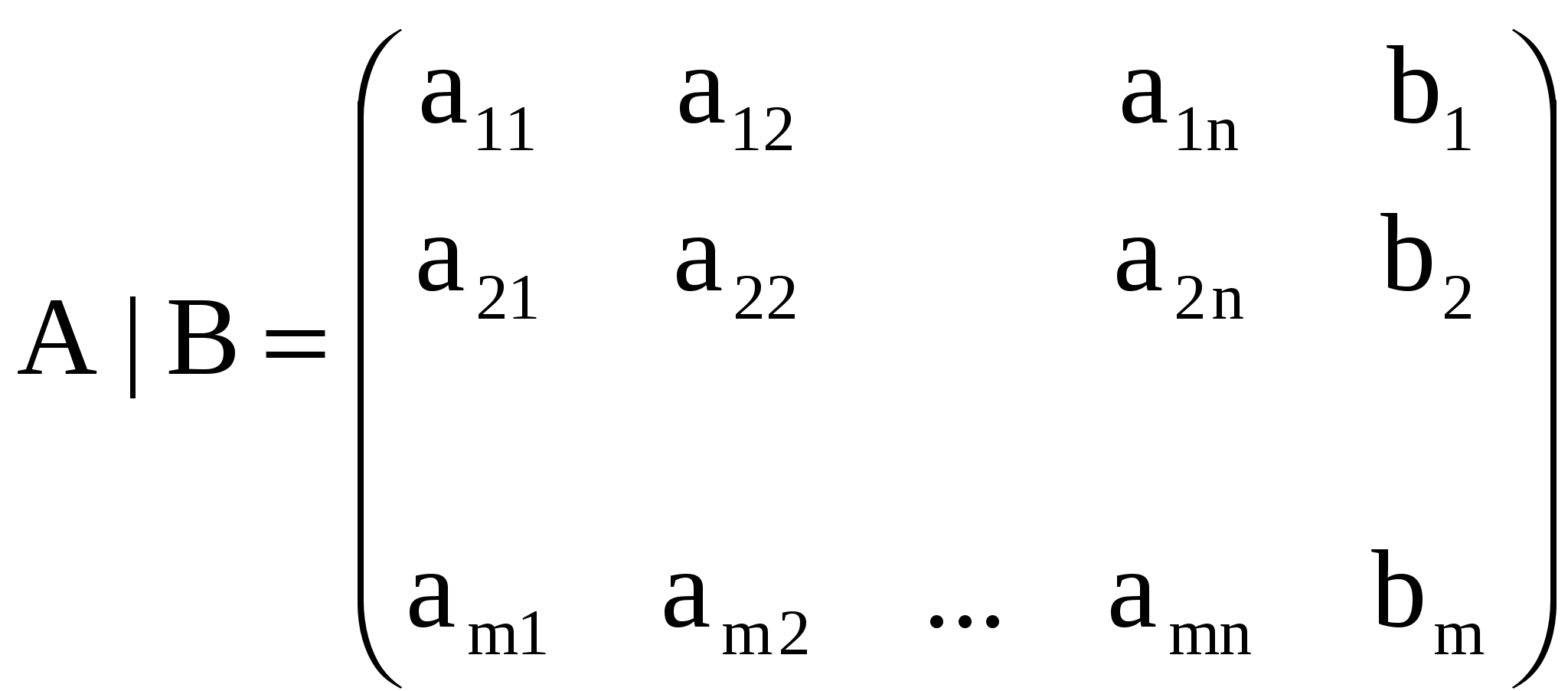



Задумаемся, что будет, если подвергнуть расширенную матрицу системы рассмотренным ранее элементарным преобразованиям строк матрицы:

а) отбрасыванию нулевых строк;

б) умножению всех элементов строки на число, отличное от нуля;

в) изменению порядка строк;

г) прибавлению к каждому элементу строки соответствующих элементов другой строки, умноженных на любое число.

Применительно к системе уравнений они сведутся к умножению обеих частей уравнений на одинаковые числа, сложению уравнений друг с другом и перестановке уравнений местами (ну а нулевая строка означает, что соответствующее уравнение вообще исключено из системы). Таким образом, применяя к системе уравнений элементарные преобразования строк, мы получим равносильную систему.

Столбцы матрицы системы тоже можно менять местами. По сути это сведется к перемене местами слагаемых в уравнениях. Впоследствии следует не забыть, что соответствующие переменные поменялись местами (т.е. при умножении преобразованной матрицы на столбец переменных последний тоже надо изменить).