Лекции по математике- часть 6. Операции над матрицами 3 Определители матриц 7

• Название: Операции над матрицами 3 Определители матриц 7
• Анкор: Лекции по математике- часть 6.doc
• Дата: 28.01.2017
• Размер: 1.01 Mb.
• Имя файла: Лекции по математике- часть 6.doc
• Тип: Документы; #716
• страница: 7 из 8

Методы решения систем линейных уравнений

Рассмотрим вначале случай, когда число уравнений равно числу переменных, т.е. m = n. Тогда матрица системы - квадратная, а ее определитель называют определителем системы.

Метод обратной матрицы

Рассмотрим в общем виде систему уравнений АХ = В с невырожденной квадратной матрицей А. В этом случае существует обратная матрица А^-1. Домножим слева обе части на А^-1. Получим А^-1АХ = А^-1В. Отсюда ЕХ = А^-1В и

Х = А^-1В.

Последнее равенство представляет собой матричную формулу для нахождения решения таких систем уравнений. Использование этой формулы получило название метода обратной матрицы
Например, решим этим методом следующую систему: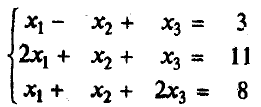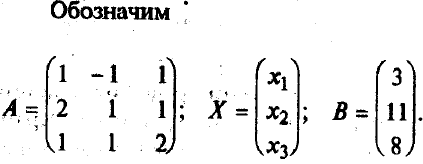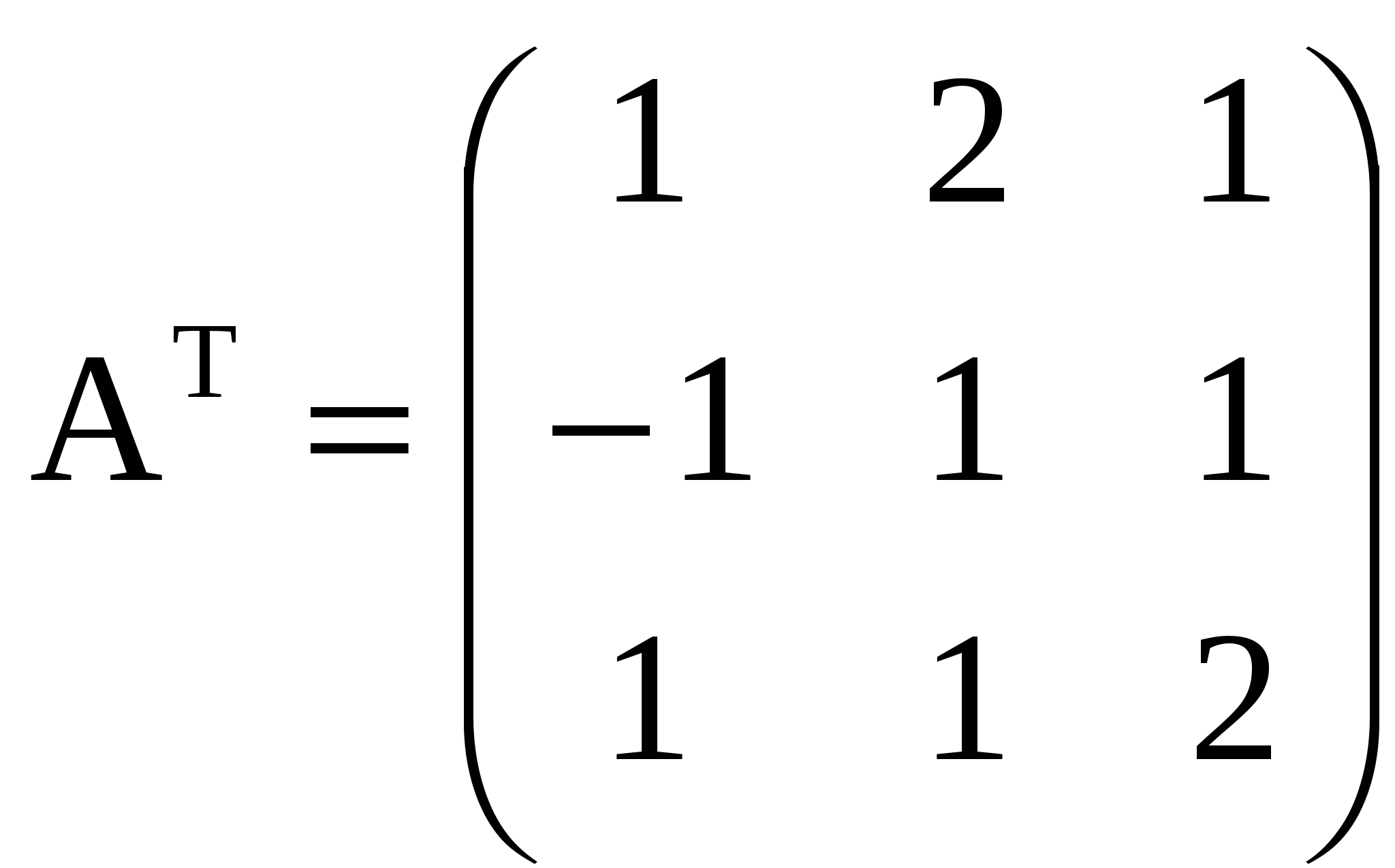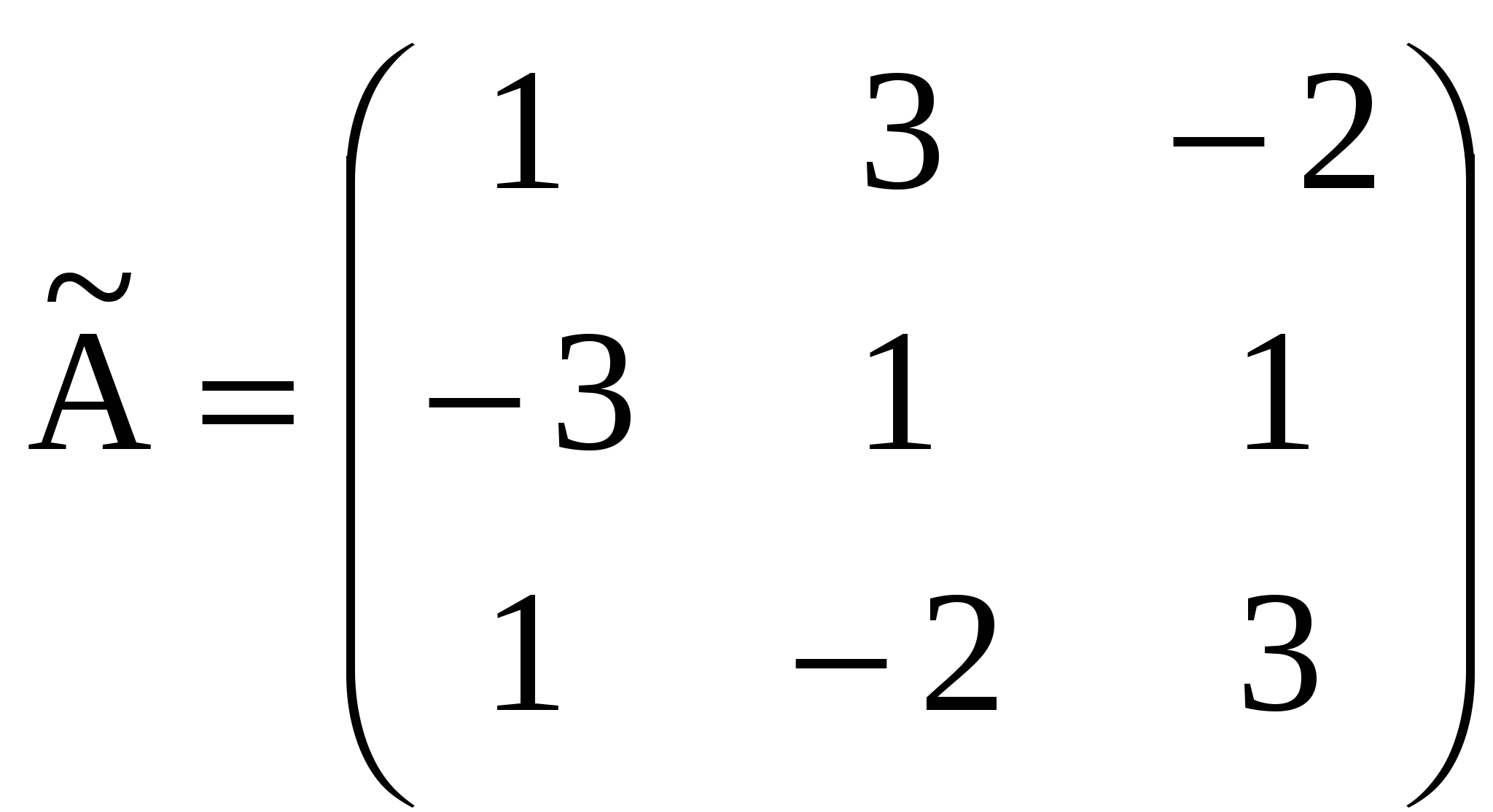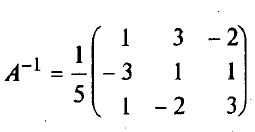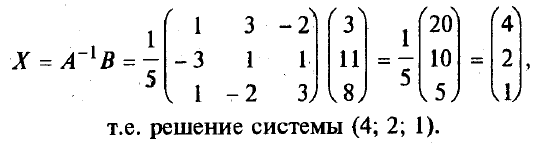







;





В конце решения системы можно сделать проверку, подставив найденные значения в уравнения системы. При этом они должны обратиться в верные равенства.

Для рассмотренного примера проведем проверку: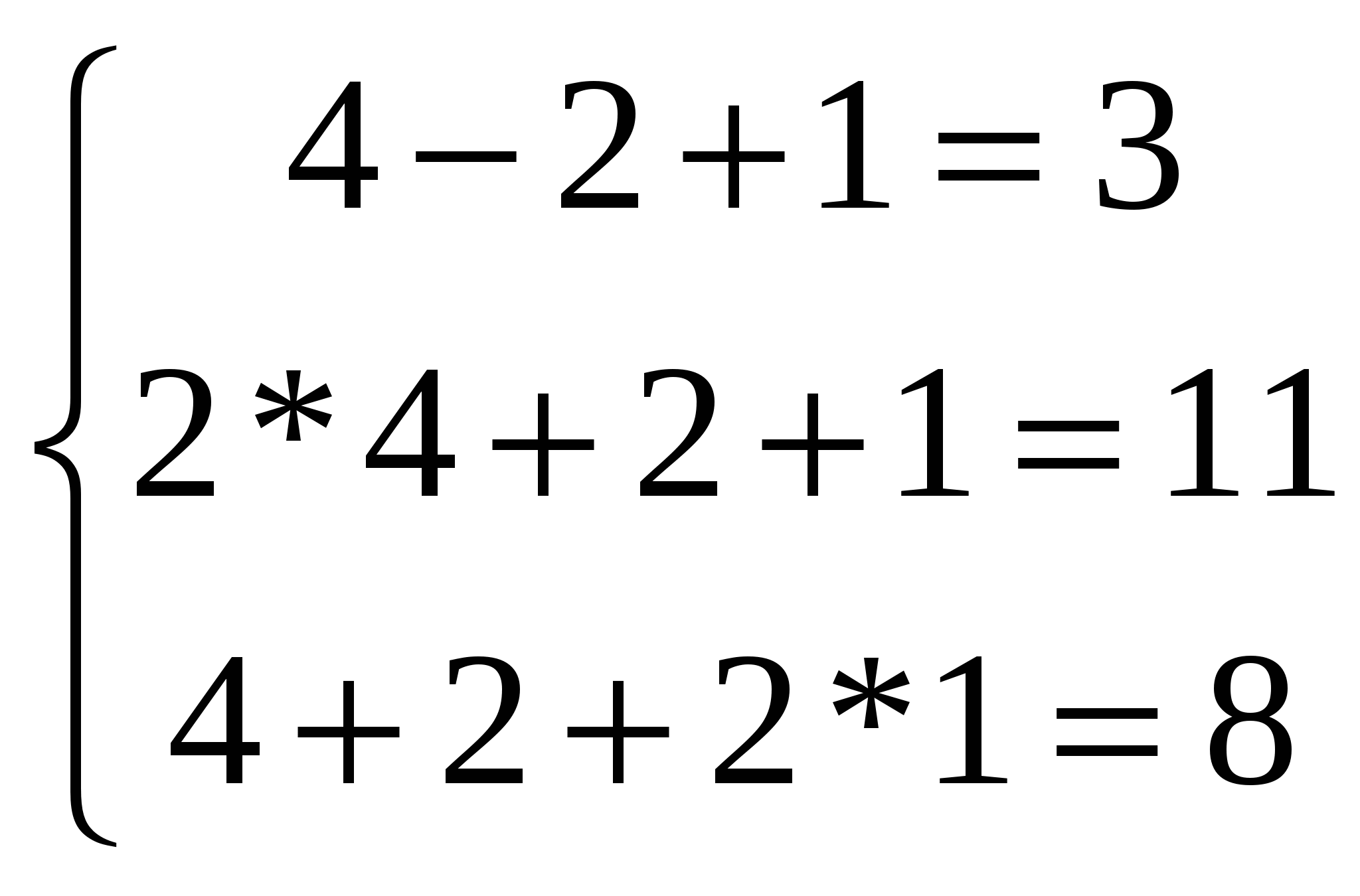

Метод решения систем линейных уравнений с квадратной матрицей по формулам Крамера

Пусть n = 2: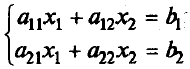



Если обе части первого уравнения умножить на a₂₂, а обе части второго – на (-a₁₂), и затем сложить полученные уравнения, то мы исключим из системы переменную x₂. Аналогично можно исключить переменную x₁ (умножив обе части первого уравнения на (-a₂₁), а обе части второго – на a₁₁). В результате получим систему: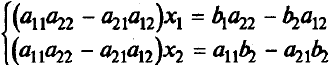



Выражение в скобках есть определитель системы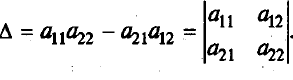



Обозначим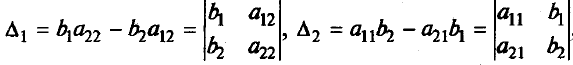



Тогда система примет вид: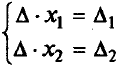



Из полученной системы следует, что если определитель системы
  0, то система будет совместной и определенной. Ее единственное решение можно вычислить по формулам:



Если  = 0, а ₁  0 и/или ₂  0, то уравнения системы примут вид 0*х₁ = ₂ и/или0*х₁ = ₂. В этом случае система будет несовместной.

В случае, когда  = ₁ = ₂ = 0, система будет совместной и неопределенной (будет иметь бесконечное множество решений), так как примет вид: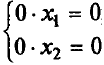


Теорема Крамера (доказательство опустим). Если определитель матрицы системы n уравнений  не равен нулю, то система имеет единственное решение, определяемое по формулам:

,

где _j - определитель матрицы, получаемой из матрицы А заменой j-го столбца столбцом свободных членов.
Вышеприведенные формулы называют формулами Крамера.
В качестве примера решим этим методом систему, которую до этого решали методом обратной матрицы: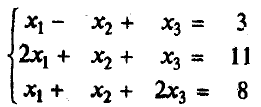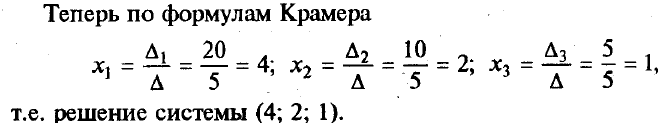








Недостатки рассмотренных методов:

1) существенная трудоемкость (вычисление определителей и нахождение обратной матрицы);

2) ограниченная область применения (для систем с квадратной матрицей).

Реальных экономические ситуации чаще моделируются системами, в которых число уравнений и переменных довольно значительное, причем уравнений больше, чем переменных Поэтому на практике более распространен следующий метод.