Лекции по математике- часть 6. Операции над матрицами 3 Определители матриц 7
 Скачать 1.01 Mb. Скачать 1.01 Mb.
|
|
Линейная алгебра 2 Матрицы 2 Операции над матрицами 3 Определители матриц 7 Обратная матрица 14 Ранг матрицы 17 Линейная независимость 22 Системы линейных уравнений 24 Методы решения систем линейных уравнений 28 Метод обратной матрицы 28 Метод решения систем линейных уравнений с квадратной матрицей по формулам Крамера 29 Метод Гаусса (метод последовательного исключения переменных) 32 Линейная алгебраМатрицыМатрица размера m х n – это прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы. Матрицы принято обозначать заглавными латинскими буквами, а элементы – теми же, но строчными буквами с двойной индексацией. Например, рассмотрим матрицу А размерности 2 х 3: В этой матрице две строки (m = 2) и три столбца (n = 3), т.е. она состоит из шести элементов aij, где i - номер строки, j - номер столбца. При этом принимает значения от 1 до 2, а от одного до трех (записывается Матрицы А и В одного размера (m х n ) называют равными, если они поэлементно совпадают, т.е. aij = bij для Матрица-строка – это матрица, состоящая из одной строки, а матрица-столбец – это матрица, состоящая из одного столбца. Например, Квадратная матрица n-го порядка – это матрица, в число строк равно числу столбцов и равно n. Например, Диагональные элементы матрицы – это элементы, у которых номер строки равен номеру столбца (aij, i = j). Эти элементы образуют главную диагональ матрицы. В предыдущем примере главную диагональ образуют элементы a11= 3 и a22= 5. Диагональная матрица – это квадратная матрица, в которой все недиагональные элементы равны нулю. Например, 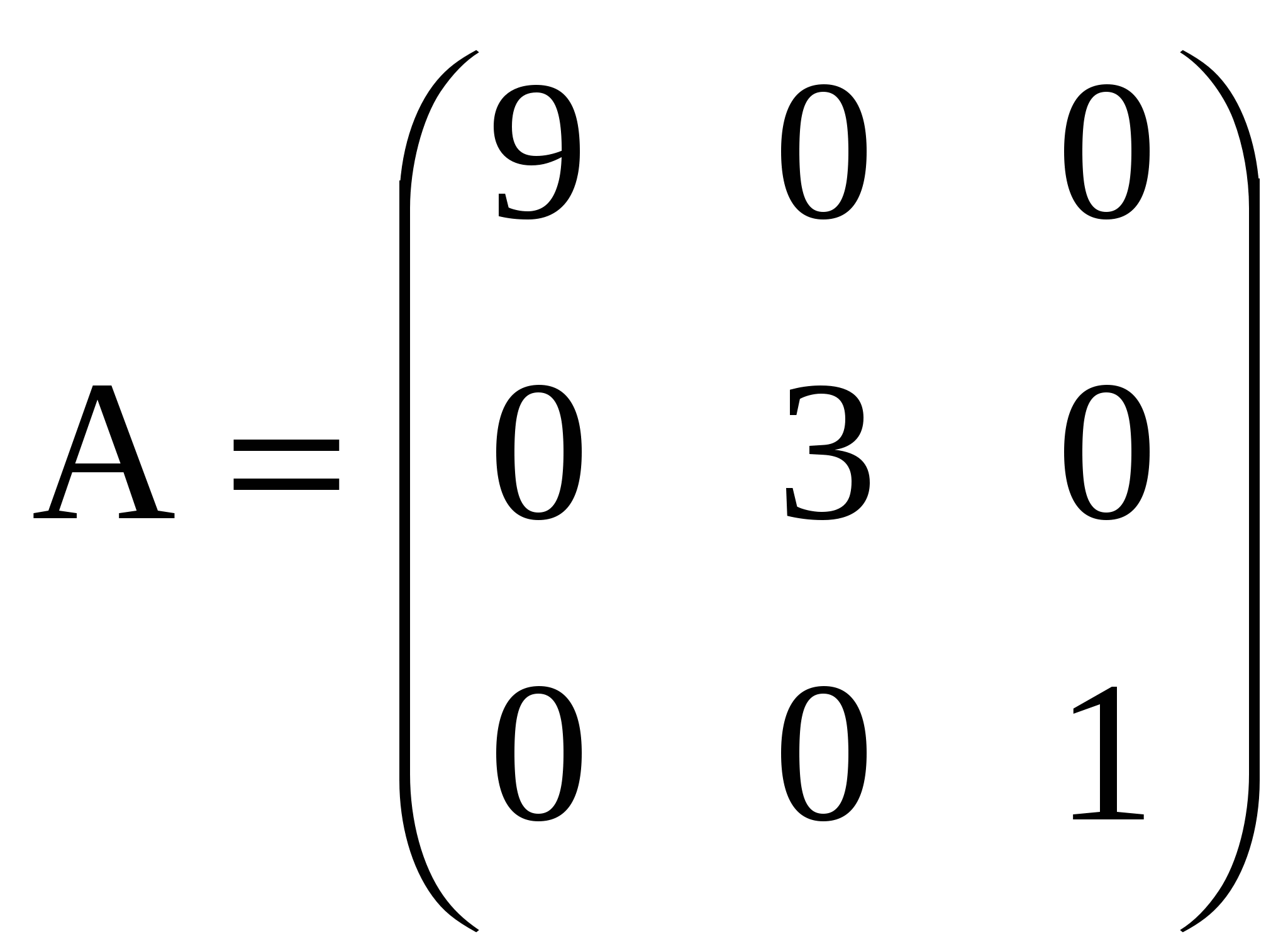 - диагональная матрица третьего порядка. Если при этом все диагональные элементы равны единице, то матрица называется единичной (обычно обозначаются буквой Е). Например, - диагональная матрица третьего порядка. Если при этом все диагональные элементы равны единице, то матрица называется единичной (обычно обозначаются буквой Е). Например, 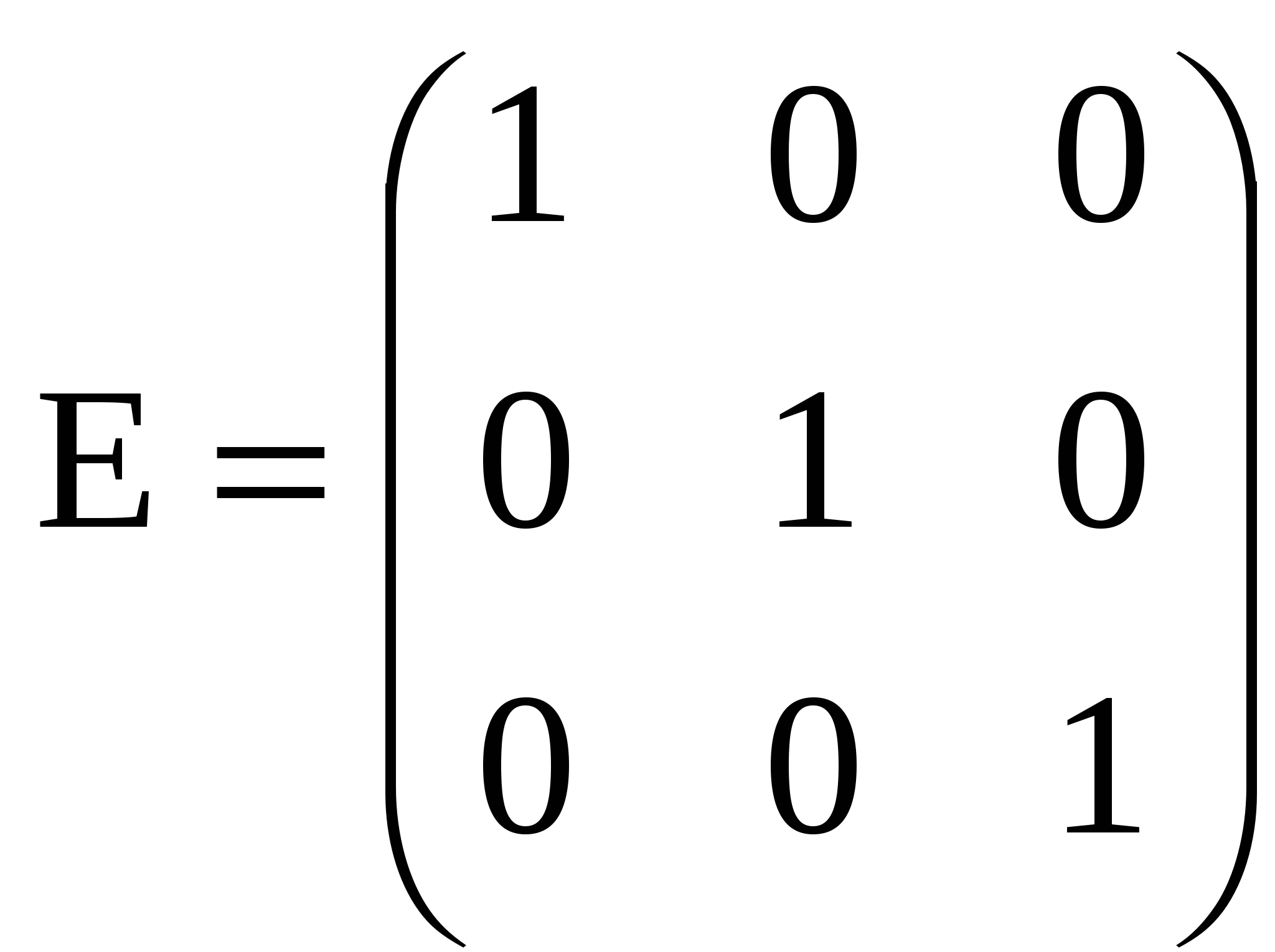 - единичная матрица третьего порядка. - единичная матрица третьего порядка.Матрица называется нулевой, если все ее элементы равны нулю. Квадратная матрица называется треугольной, если все ее элементы ниже (или выше) главной диагонали равны нулю. Например,  - треугольная матрица третьего порядка. - треугольная матрица третьего порядка.Операции над матрицамиНад матрицами можно производить следующие операции: 1. Умножение матрицы на число. Произведением матрицы А на число называется матрица В = А, элементы которой bij = aij для любых i и j. Например, если 2. Сложение матриц. Суммой двух матриц А и В одинакового размера m х n называется матрица С = А + В, элементы которой сij = aij + bij для i, j. Например, если Отметим, что через предыдущие операции можно определить вычитание матриц одинакового размера: разность А-В = А + (-1)*В. 3. Умножение матриц. Произведением матрицы А размера m x n на матрицу В размера n x p называется такая матрица С, каждый элемент которой сij равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В, т.е. Например, если 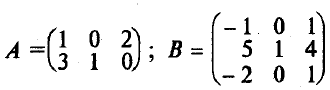 , то размер матрицы-произведения будет 2 x 3, и она будет иметь вид: , то размер матрицы-произведения будет 2 x 3, и она будет иметь вид: 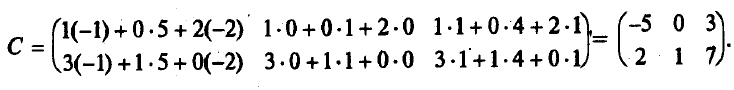 В этом случае матрица А называется согласованной с матрицей В. На основе операции умножения для квадратных матриц определена операция возведения в степень. Целой положительной степенью Аm (m > 1) квадратной матрицы А называются произведение m матриц, равных А, т.е. Подчеркнем, что сложение (вычитание) и умножение матриц определены не для любых двух матриц, а только для удовлетворяющим определенным требованиям к своей размерности. Для нахождения суммы или разности матриц их размер обязательно должен быть одинаковым. Для нахождения произведения матриц число столбцов первой из них должно совпадать с числом строк второй (такие матрицы называют согласованными). Рассмотрим некоторые свойства рассмотренных операций, аналогичные свойствам операций над числами. 1) Коммутативный (переместительный) закон сложения: А + В = В + А 2) Ассоциативный (сочетательный) закон сложения: (А + В) + С = А + (В + С) 3) Дистрибутивный (распределительный) закон умножения относительно сложения: (А + В) = А + В А (В + С) = АВ + АС (А + В) С = АС + ВС 5) Ассоциативный (сочетательный) закон умножения: (АВ) = (А)В = А(В) A(BС) = (АВ)С Подчеркнем, что переместительный закон умножения для матриц в общем случае НЕ выполняется, т.е. AB BA. Более того, из существования AB не обязательно следует существование ВА (матрицы могут быть не согласованными, и тогда их произведение вообще не определено, как в приведенном примере умножения матриц). Но даже если оба произведения существуют, они обычно разные. В частном случае коммутативным законом обладает произведение любой квадратной матрицы А на единичную матрицу того же порядка, причем это произведение равно А (умножение на единичную матрицу здесь аналогично умножению на единицу при умножении чисел): АЕ = ЕА = А В самом деле, 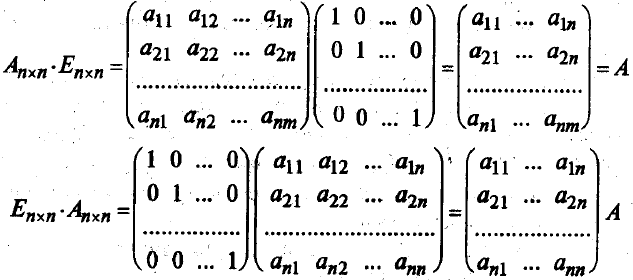 Подчеркнем еще одно отличие умножения матриц от умножения чисел. Произведение чисел может равняться нулю тогда и только тогда, когда хотя бы одно из них равно нулю. О матрицах этого сказать нельзя, т.е. произведение ненулевых матриц может равняться нулевой матрице. Например, 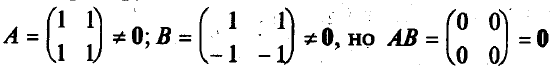 Продолжим рассмотрение операций над матрицами. 4. Транспонирование матрицы представляет собой операцию перехода от матрицы А размера m x n к матрице АТ размера n x m, в которой строки и столбцы поменялись местами: 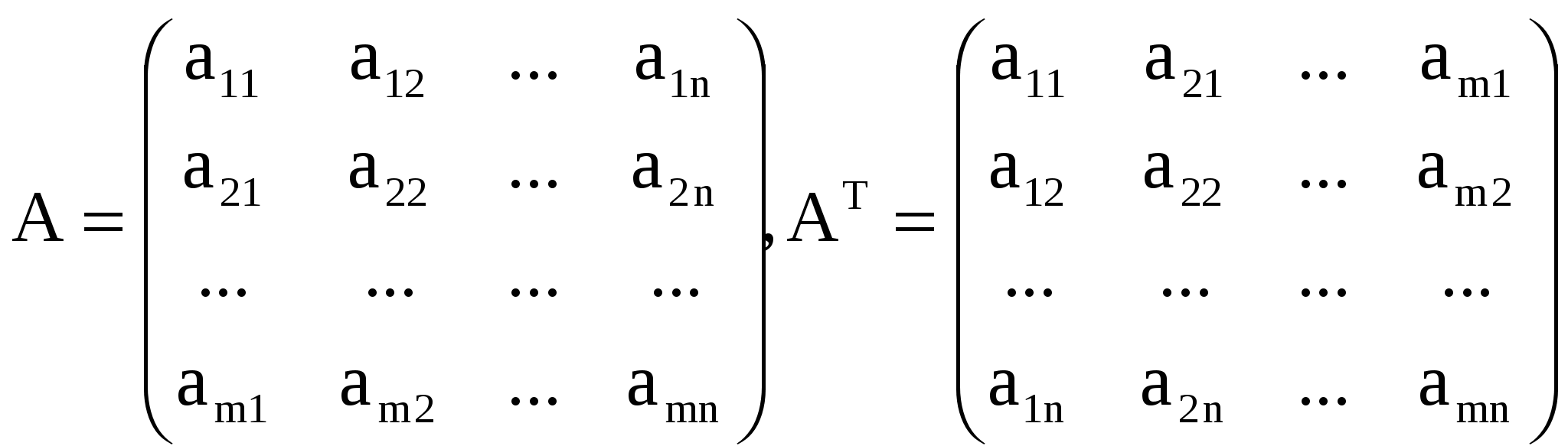 %. %. Свойства операции транспонирования: 1) Из определения следует, что если матрицу транспонировать дважды, мы вернемся к исходной матрице: (AT)T = A. 2) Постоянный множитель можно вынести за знак транспонирования: (А)T = АT. 3) Транспонирование дистрибутивно относительно умножения и сложения матриц: (AB)T = BTAT и (A + B)T = BT + AT. |
