Поддерж. очист. пр-ва целиками. Определение напряжений в нетронутом массиве горных пород при гористом рельефе поверхности

• Название: Определение напряжений в нетронутом массиве горных пород при гористом рельефе поверхности
• Дата: 12.08.2022
• Размер: 2.58 Mb.
• Имя файла: Поддерж. очист. пр-ва целиками.docx
• Тип: Документы; #644516
• страница: 2 из 16

Определение напряжений в нетронутом массиве горных пород при равнинном рельефе поверхности

В 1878 г. швейцарский геолог А. Гейм сделал предположение, что вертикальная составляющая напряжений Ϭ_z на глубине Н. определяемая гравитационными силами, равна или пропорциональна весу вышележащих пород, т/м² 



Где ɣ— удельный все пород.

Наличие п величину горизонтальных напряжений он ставил в зависимости от действующих гравитационных сил и остаточных касательных напряжений, обусловленных горообразовательными процессами, и рекомендовал находить их из следующего выражения:



где т — коэффициент бокового распора.



Швейцарский ученый А. Гейм Впервые гипотезу о гидростатическом распределении напряжений в массиве высказал в XIX в. швейцарский геолог Альберт Гейм. Изучая складчатые геологические структуры Альп, он обратил внимание на признаки пластического течения горных пород. Следовательно, предположил А. Гейм, поведение горных пород в геологических масштабах времени (миллионы лет) можно уподобить течению очень вязкой жидкости с очень маленькой скоростью. А если в некотором смысле толща пород подобна вязкой жидкости, то и распределение напряжений в ней должно быть гидростатическим, как в жидкости.

В общем случае, когда массив слагается из горных пород различного веса и строения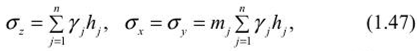



где ɣ— соответственно удельный вес, т -мощность и коэффициент бокового распора 1-го слоя пород.

Динник Александр Николаевич (1876-1950) — ученый в области горной науки, академик АН СССР (1946) и АН УССР (1929). В 1899 г. окончил Киевский университет. В 1900-1904 гг. занимался преподавательской работой (Киев, Донецк, Днепропетровск), в 1941-1950 гг. заведовал отделом теории упругости Института горной механики АП УССР. Член Президиума АН УССР (1944-1948). Создал школу в области прикладной математики, теории упругости и колебаний, одним из приложений которой является разработка теории горного давления, искривления скважин, расчета шахтных крепей, изучение динамических процессов в шахтных канатах, создание методов их испытаний и безопасной эксплуатации.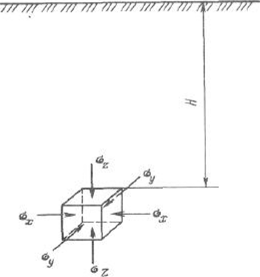

 

Рис. 1.18. Схема к определению напряжений в нетронутом массиве

В 1925 г. академик А. Н. Динник, рассматривая массив горных пород как упругую изотропную среду, находящуюся в гравитационном силовом поле, предложил решение задачи опсрсдслсния вертикального и горизонтального напряжения в элементарном объеме породы, расположенного на глубине Я (рис. 1.18).

Принимая вертикальную составляющую а = ɣН и учитывая, что относительные горизонтальные деформации изменятся по обобщенному закону Гука для плоской модели: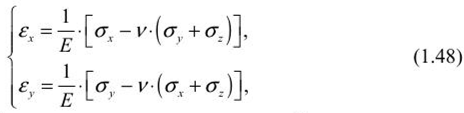



равны между собою и равны нулю, т. с. в_Л = в,. = 0 и ст_д = а,,, можно записать: 

то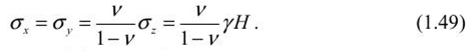



Следовательно, коэффициент бокового распора:



где v — коэффициент поперечной деформации.

При V = 0,25, что свойственно многим породам, т = 1/3.

Исходя из гипотезы А. Н. Динника, в гравитационном силовом поле, на любой глубине т <7 < а. > а_г.

Учитывая совместное влияние гравитационных и тектонических сил, величину горизонтальных напряжений необходимо определять как сумму остаточных сг^,<т' и неотсктонических <т" о" напряжений, а также горизонтальной составляющей гравитационных сил (/"o'”, т .е.с_х=о'_х+о';₊о'”а_у=о'_у+о';+о';.

Практически величины о_д, о, определяются путем статистической обработки данных многочисленных натурных измерений. В результате выполнения такой работы в Институте физики и механики горных пород АП Кыргызстана были получены эмпирические зависимости изменения горизонтальных напряжений, МПа, для глубин нс более 1000 м:

в крепких породах, когда Е изменяется от (5-6) - 10⁴ до (10-11) -10⁴ МПа: 


в породах средней прочности при изменении Е (2-3)-10⁴ до (5-6)- 10⁴ МПа:



Эти зависимости справедливы при среднем значении плотности пород у ⁼ 2,7 • 10³ кг/м³.

Подобные исследования проводились в зарубежных странах. Они показывают, что горизонтальные напряжения не равны между собою. Имеются эмпирические зависимости для определения повышенных горизонтальных напряжений о., в зависимости от глубины (до 1000 м) для отдельных территорий: Северной Америки (Хеймсон) о.. = 0,0196Н + 5,0 МПа; Канадского щита (Г. Хэргст) о,, = 0,04Н+ 8,139 МПа; Австралия (Г. Воротницкий, Д. Денхам) а, = 0,0215Н + 7,260 МПа.

Из рассмотренного следует, что для определения полного тензора напряжений нетронутого массива требуется проведение комплексных исследований на различных участках месторождения в течение длительного времени, так как одиночные замеры не могут дать исчерпывающей информации о напряженности массива горных пород.