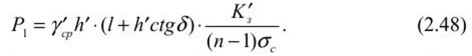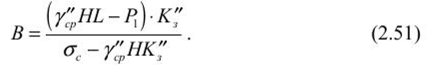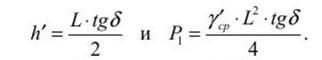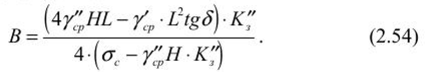Поддерж. очист. пр-ва целиками. Определение напряжений в нетронутом массиве горных пород при гористом рельефе поверхности

• Название: Определение напряжений в нетронутом массиве горных пород при гористом рельефе поверхности
• Дата: 12.08.2022
• Размер: 2.58 Mb.
• Имя файла: Поддерж. очист. пр-ва целиками.docx
• Тип: Документы; #644516
• страница: 8 из 16

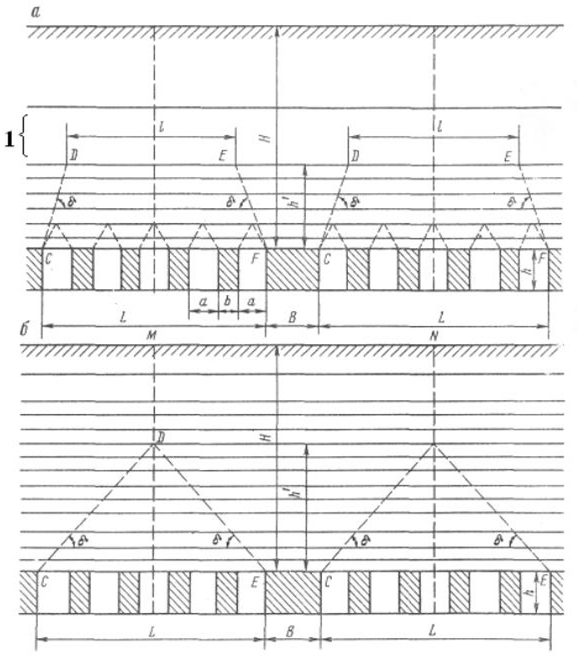
Определение размеров целиков при крутом падении рудных тел

При отработке крутопадающих залежей оставляются нс только междублоковые (междукамерныс), но и междуэтажные целики, распределение нагрузки на которые зависит от соотношения подработанных камерами площадей, мощности налегающих пород, угла падения и других факторов.

При глубинах разработки до 500-700 м, когда целики оставляются на весь период эксплуатации рудника и длина фронта подработки висячего бока камерами составляет нс менее 0,7-0,8% от глубины работ, предполагается, что междукамерныс целики испытывают давление со стороны призм сползания пород висячего бока и нригружа- ются обрушенными сверху породами. Расчетная схема, предложенная С. Г. Борисенко, представлена на рисунке 2.7, для случая камерных систем разработки.

Вес призмы сползания KLMN, приходящийся на целик:



где d = /г_н sin (а + Р) — толщина призмы; /;_н — наклонная высота этажа; а •— угол падения рудного тела; (5 — угол сползания призмы.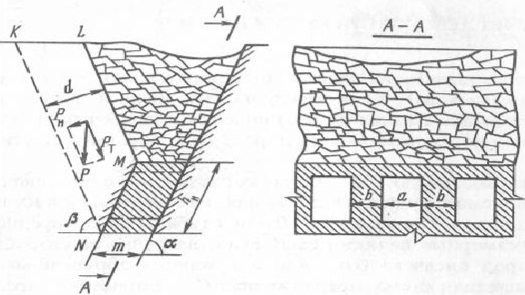



Рис. 2.7. Схема к определению размеров целиков при крутом падении рудных тел (по С. Г. Борисенко)

Тангенциальная составляющая силы веса р Р_т направлена вдоль линии сдвижения KN и определяется из условия



Составляющую веса призмы сползания Р_х, направленную нормально к наклонной длине междукамерного целика h,„ можно найти из формулы 

Из условия прочности целика определяется его ширина

   

В расчетах необходимо учитывать связь призмы сползания с окружающим массивом. Поэтому тангенциальная составляющая должна быть уменьшена на величину противодействующих сил трения и сцепления по поверхностям призмы сползания:



где С — сцепление; (р — угол внутреннего трения; Р_н — нормальная составляющая.

Тогда формула (2.34) принимает следующий вид: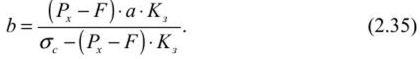



Действие силы трения и сцепления при расчете целиков особенно важно учитывать в случае разработки залежей небольшой длины и «слепых» рудных тел.

Определение размеров целиков на основании гипотезы свода давлении

В этом случае предполагается, что в породах над выработанным пространством образуется свод давления (естественного равновесия). Максимальные нагрузки приходятся на целики, находящиеся в средней части пролета. Нагрузка на отдельный целик определяется весом пород, расположенных над ним в пределах свода давления (рис. 2.8). Вес от пород, расположенных выше свода давления, воспринимается разгружающим сводом и передается в виде опорного давления на прилегающие краевые зоны рудного массива.

Возможность использования гипотезы свода для расчета целиков при разработке рудных месторождений подтверждается работами многих ученых (М. М. Протодьяконова, П. И. Городецкого, С. В. Ветрова и др.). Опытами на моделях из эквивалентных материалов (ВНИМИ) установлено, что расчеты целиков на основании гипотезы свода можно приводить в том случае, когда пролет подработки пород нс превышает (0,7-0,8) Н.

Целики рассчитываются для наиболее неблагоприятных условий (средней части подрабатываемой площади).

Условие предельного равновесия в этом случае можно записать в виде 

где S„ — площадь целика; S' — площадь пород, приходящихся на целик; а,. — предел прочности на сжатие материала целика; K_s — коэффициент запаса прочности целика; а — угол падения залежи; 1г_с„ — высота свода давления в средней части пролета.

Отсюда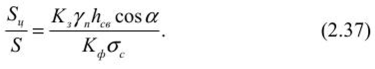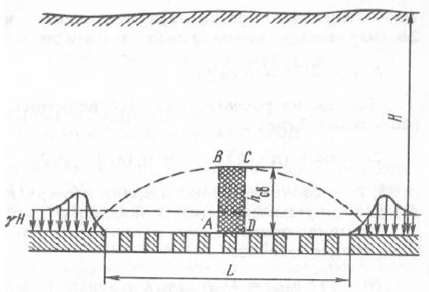 



Рис. 2.8. Схема для определения размеров целиков по теории свода

Используя соотношение SJS для целиков различной формы, можно определить ширину целика.

В случае оставления барьерных целиков С. В. Ветров предлагает рассчитывать целики, основываясь на схеме расположения сводов, показанной на рисунке 2.9.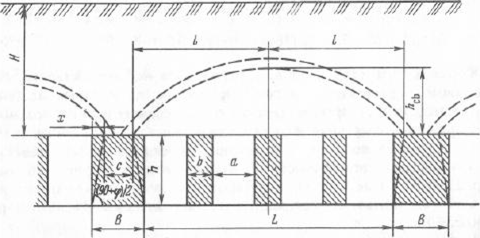



Рис. 2.9. Схема для определения размеров междукамерных и барьерных (панельных) целиков (по С. П. Ветрову)

Если в отрабатываемой панели (или шахтном поле) имеется п камер, то им будет соответствовать (и - 1) целиков. Площадь всех целиков (п - 1) S„. Bee пород в параболическом своде над целиками на пролете 2b (на единицу длины целика) определим из выражения



Исходя из расчетной схемы, величина пролета свода естественного равновесия будет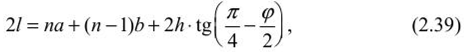



где а, b — соответственно ширина камеры и целика, h — высота камеры, (о — угол внутреннего трения массива руды.

Условие предельного равновесия системы междукамерные целики — свод имеет вид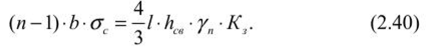



Из (2.40) ширина междукамерного целика



Коэффициент запаса прочности принимается с учетом срока существования целиков и влияния конкретных условий отработки.

Давление на барьерный целик определяется весом столба пород до поверхности (за исключением веса пород в пределах параболического свода). Нагрузка на 1 м барьерного целика шириной В составляет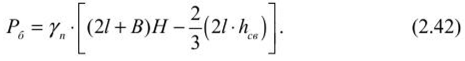



Условие работы барьерного целика е запасом прочности будет 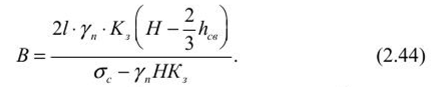  После подстановки и преобразований выражение (2.43) примет вид



Форма и параметры сводов, образующихся над выработанным пространством, определяются многими причинами, из которых особенно следует выделить свойства и строение пород, ширину пролета подработки, напряженное состояние пород кровли и др.

Исследования проф. А. А. Борисова, относящиеся к слоистым осадочным породам, показывают, что высота свода в средней его части b = (0,21-0,3) / (где / — пролет выработки). В полученных нами результатах по моделированию однородных трещиноватых изверженных пород Ь= (0,55-0,65) /.

Многие исследователи считают, что форма свода зависит от прочности массива пород на растяжение. Вследствие того, что деформации растяжения обратно пропорциональны прочности пород и снижаются с увеличением сцепления и коэффициента внутреннего зрения, высота свода будет возрастать при уменьшении прочности массива пород.

Особенности определения параметров целиков при слоистом строении налегающих пород При определении размеров целиков можно воспользоваться расчетными схемами Ю. А. Модестова в зависимости от неоднородного или однородного строения кровли, в основу которых заложена теория свода. При неоднородном строении слоистой кровли и наличии «породы — моста» междукамерные целики находятся только под нагрузкой веса пород, заключенных в призме с трапецевидным основанием CDEF (рис. 2.10, а). В том случае, когда верхнее основание трапеции DE = I меньше величины первого предельного пролета L (по В. Д. Слесареву), т. е. когда «порода — мост», воспринимая нагрузку от веса вышерасположенных пород, нс испытывает растягивающих деформаций. На междукамерные целики будет передаваться только вес пород в трапеции CDEF. Угол наклона боковых сторон трапеции 5 принимается в зависимости от прочности пачки слоев. Тогда вес пород, приходящийся на междукамерные целики на подработанном пролете, будет: где /?' — мощность пород кровли от пласта до породы-моста. Подставляя значение L =1 + 2h' ctg 3, получим: В случае п камер число целиков будет (п - 1) и условие предельного равновесия можно записать в виде равенства где (Тс — предел прочности на сжатие целика (в массиве); К' — коэффициент запаса прочности для междукамерных целиков. Отсюда: На барьерный целик, разделяющий соседние шахтные поля (или участки), приходится полный вес пород до поверхности за исключением Р  где Я — мощность налегающей толщи; В — ширина барьерного целика; Y’v — среднее значение удельного веса пород. Ширина барьерного целика В находится из равенства где К" — коэффициент запаса прочности для барьерных целиков. Подставляя значение Pi, и решая равенство относительно Ь, получим:  Рис. 2.10. Схемы к определению размеров целиков при наличии (а) и отсутствии (б) породы — моста (1) В случае однородного строения слоистой кровли расчетную схему можно представить в следующем виде (см. рис. 2.10, б). Из-за отсутствия «породы — моста» на междукамерные целики приходится все пород, заключенных в трехгранных призмах CDE, а на барьерные — вес толщи пород до поверхности (за исключением веса пород над подработанными пролетами). Высота треугольника в основании и вес трехгранной призмы соответственно будут: Подставляя значение Pi в выражение (2.47), получим Принимая во внимание (2.49), все пород, приходящийся на барьерный целик, будет  Из условия (2.50) после подстановки в него значения Р2 можно найти ширину барьерного целика: