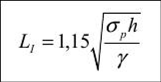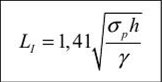Поддерж. очист. пр-ва целиками. Определение напряжений в нетронутом массиве горных пород при гористом рельефе поверхности

• Название: Определение напряжений в нетронутом массиве горных пород при гористом рельефе поверхности
• Дата: 12.08.2022
• Размер: 2.58 Mb.
• Имя файла: Поддерж. очист. пр-ва целиками.docx
• Тип: Документы; #644516
• страница: 10 из 16

Основные положения определении устойчивых пролетов камер

При разработке рудных месторождений к устойчивости кровли камерных выработок предъявляются высокие требования: во-первых, с позиций обеспечения безопасности работ; во-вторых — полноты извлечения полезного ископаемого. Правилами технической эксплуатации рудников применение систем разработки с открытым очистным пространством допускается при устойчивых и весьма устойчивых рудах и породах. К устойчивым породам отнесены такие, при которых площадь обнажения достигает 600 м², а весьма устойчивым — до 1000 м² и более.

Устойчивость подрабатываемых горных пород зависит от их строения, физико-механических свойств и действующих нагрузок, что правомерно и для кровли камер.

Кровля камер испытывает сложное напряженное состояние. В том случае, когда она представлена однородными породами (или близкими к ним по деформационно-прочностным характеристикам) и целики полностью сохраняют сцепление с массивом, в средней части пролета камеры возникают растягивающие, а в областях, примыкающих к целикам, сжимающие напряжения.

Для расчета пролетов камер, кровля которых представлена слоистыми породами, обычно пользуются методами строительной механики, используют теорию балок и плит.

Считается, что в случае слоистого строения пород пролет камеры будет надежно устойчивым, если слои непосредственной кровли испытывают только упругие деформации, т. с. ширина камеры не превышает величины первого предельного пролета по В. Д. Слесаре- ву. Несущая способность слоистой кровли частично сохраняется и в запредельном состоянии пород, когда посередине пролета камеры и у целиков появляются трещины разрыва — ширина камеры соответствует второму предельному пролету.

При однородных трещиноватых породах пролет камеры будет устойчивым тогда, когда в кровле образуется свод естественного равновесия. Поэтому в породах, склонных к сводообразованиям, кровле камер рекомендуется придавать сводчатую форму с параметрами, соответствующими своду естественного равновесия.

Потеря устойчивости кровли проявляется в виде отслоений и вывалов в результате технологического трещинообразования или при постепенном развитии пластических деформаций пород кровли.

Для повышения устойчивости кровля камер укрепляется анкерами (штангами), химическими составами, цементными растворами, набрызг-бетоном.

Определение пролета камеры на основании гипотезы свода

Теоретические основы сводообразования в однородных горных породах впервые были разработаны профессором Рижского политехникума В. Риттером в 1879 г. Было установлено, что породы над выработкой отделяются как единое целое в форме свода, благодаря появляющимся в них растягивающим напряжениям, превосходящим предел прочности материала на разрыв. В породах, обладающих сцеплением, над выработкой образуется свод, отделяющийся по кривой А СВ (рис. 2.11, а) вследствие преодоления усилия а„ ds, направленного нормально к поверхности свода (где а_р — предел прочности на разрыв; ds — элементарный участок дуги). Вес пород в своде давления определяется из выражения 

Учитывая, что вертикальная составляющая сопротивления разрыву MN = <т ? dSjcos (X, общее сопротивление разрыву по поверхности свода будет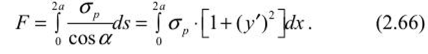



Сводообразование возможно, если Q > F, т. е. когда в своде давления (обрушения) действует сила: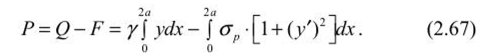



Исследуя выражение (2.67) по у, можно убедиться, что кривая свода уставляет собою параболу:



а^у

с высотой Ь =- при х = а (здесь а — полупролст камеры).

Ла_р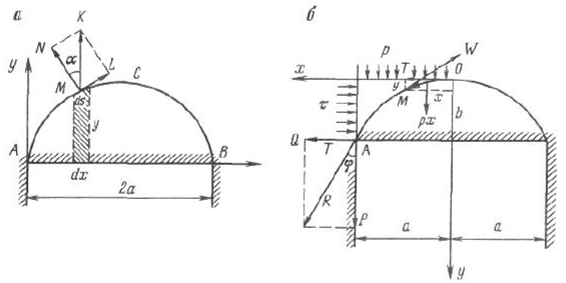



Рис. 2.11. Расчетные схемы теории свода по В. Риттеру (а) и по М. М. Протодьяконову (б)

При Q = F можно определить ширину выработки, при которой свод давления не образуется и породы кровли нс будут давить на крепь выработки (условие предельного равновесия). Такое условие,

(7„

по В. Риттеру, соблюдается, сели 2а < 7 — .

Г

Из теории В. Риттера следует, что своды образуются при определенных соотношениях удельного веса пород, прочности пород на разрыв и величины пролета выработки (камеры). Свод отрывается от массива в виде сплошного тела.

Проф. М. М. Протодьяконов на основании анализа предыдущих работ по исследованию механизма сводообразования пород и большого объема собственных опытных работ теорию сводообразования разработал более детально.

Согласно расчетной схеме Протодьяконова (см. рис. 2.11, б) на любую левую часть свода действуют силы горизонтальной реакции правой части свода Т, равнодействующей вертикального давления рх и реакции нижней части свода W. Равновесие рассматриваемого участка свода МО относительно точки М, координаты которой равны х и у, обеспечивается при условии 

что свидетельствует о параболической форме свода.

В опоре свода А действуют нормальная (прижимающая) сила Р и горизонтальная (сдвигающая) сила Q. Отношение Q/P = tg« = / (здесь/— коэффициент трения пород) определяет устойчивость свода. Если Q< fP, то свод будет устойчив, при О >fP произойдет его разрушение. Принимая во внимание, что Р = ра и Т = Q, условие устойчивости можно записать в виде Q< fpa или Т + тЬ =fpa (где г — горизонтальное сдвигающее усилие на единицу вертикальной проекции свода; b — высота свода).

Отсюда 

Подставляя (2.70) в выражение (2.69) в точке 0 (х = а; у = Ь), получим:



откуда после преобразований имеем



Условие максимальной устойчивости будет обеспечиваться в том случае, если г = т_тах, а

Отсюда высота свода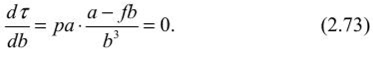 



Подставив это значение b в выражение (2.72), получим 

Принимая во внимание выражение (2.70), можно найти величину   а ю (2.69) установить, что кривая свода представляет собой параболу



М. М. Протодьяконов считает, что выражения (2.74) и (2.77) могут быть использованы для практических расчетов параметров сводов и устойчивых пролетов камер.

Зная площадь параболического свода S, можно определить вес породы на единицу длины выработки и, следовательно, давление на крепь: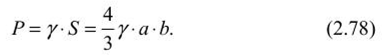 

Подставляя значение b из (2.74), имеем: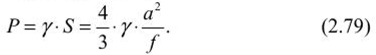



Из выражений (2.78) и (2.79) следует, что давление на крепь не зависит от глубины работ. Исследования же показывают, что до глубины Я = 10а давление на крепь возрастает, а затем снижается и остается постоянным. Поэтому при небольших глубинах расчеты по формулам М. И. Протодьяконова неприемлемы. Следует отметить, что в расчетах давления на крепь никак нс учитываются характеристики крепи и время взаимодействия системы порода — крепь.

Если же камеры остаются незакрепленными, то по теории М. М. Протодьяконова можно определить устойчивые пролеты камер с параболической формой свода. Высота свода, как свидетельствует формула (2.74), определяется прочностью пород и шириной камеры.

Определение пролетов камер при слоистом строении кровли

Слоистую кровлю камеры можно рассматривать как плиту, свободно опертую или защемленную по контуру выработки. Если длина камеры превышает ее ширину в три и более раз, то участок выреза пород поперек камеры рассматривается как балка — стенка, на которую действует равномерно распределенная нагрузка. Для учета граничных условий в направлении длины камеры истинный пролет камеры заменяется эквивалентным пролетом. Для расчетов предельных пролетов камер примсняютея методы строительной механики, рассматривающие слоистую толщу кровли камеры как упруго-пластическую среду.

Расчеты слоистой кровли камер по теории В. Д. Слссарсва выполняются при следующих допущениях:

• 
  ? обнаженная кровля выработки подобна свободно опертой или •защемленной плите;
  
• 
  ? расчет плиты можно заменить расчетом эквивалентной балки;
  
• 
  ? плиты и балка будут испытывать приблизительно одинаковое напряженно-деформированное состояние в наиболее опасных сечениях, если их гидравлические радиусы равны;
  
• 
  ? всякую выработку, ограниченную по контуру, можно заменить эквивалентной выработкой бесконечно большой длины, кровля которой будет испытывать так же напряжения и деформации, как и кровля камеры;
  
• 
  ? для расчета однонролстной балки, эквивалентной кровли горной выработки, можно использовать графический способ построения кривой давления, который применяется в статике сооружения для расчета сводов;
  
• 
  ? кровля горных выработок работает за пределами упругих и упруго-пластических деформаций (до момента потери его устойчивости).
  

Под гидравлическим радиусом понимается отношение площади обнажения камеры S ксс параметру Р, т. е.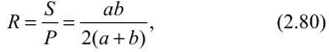



где а Ь — соответственно ширина и длина камеры.

Заменяя для расчета плиту эквивалентной балкой, можно определить гидравлический радиус выработки бесконечной большой длины, т. е.: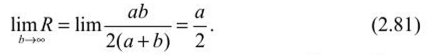



Отсюда следует, что эквивалентный пролет камерной выработки l_om = 2R. Поэтому при расчетах кровли камеры необходимо принимать балку с эквивалентным пролетом: 

Таблица 2.2

Предельные состояния слоистой кровли

Предельное состояние кровли	Характеристика состояния кровли	Предельные пролеты балки
		свободно опертой	с защемленными концами
I	В кровле отсутствуют растягивающие напряжения
и	Породы кровли испытывают максимальные деформации (прогиб)без нарушения сплошности
	Появляются трещины и возможно частичное обрушение
hi	Трещины распространяются на всю мощность кровли, и она обрушастся

Работу кровли В. Д. Слссарсв предлагает рассматривать в трех состояниях, которые он назвал предельными (табл. 2.2).

Величины Lj, Ьц, L/ц можно принимать как предельные пролеты кровли камеры, где а_р — предел прочности горной породы на разрыв кПа; h — толщина балки, м; у — удельный все породы, кг/м³.

Возможность применения расчетных методов теории плит для определения обнажений кровли в слоистых трещиноватых и нетрещиноватых породах обоснована в работах В. Д. Слссарсва, С. Г. Авершина, Г. Н. Кузнецова, А. А. Борисова и др. На практике наибольшее распространение получил метод расчета по теории тонких плит при соотношении /(//<1/5 и до /(//<1/3, где /( — толщина плиты, / — ширина плиты (камеры).

Для кровли, сложенной однородными трещиноватыми горными породами, величина устойчивого пролета для одного слоя определяется из зависимости



где % — коэффициент ползучести породы при сжатии, принимается ?= 0,5 —0,7; а, — расстояние между трещинами в направлении, нормальном к поверхностям системы трещин наибольшего ослабления (толщина слоя, пролет которого определяется); К, — запас несущей способности породного слоя (рекомендуется К, = 4).

С учетом угла наклона трещин наибольшего ослабления или падения слоев а предельный пролет I/ определим из выражения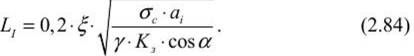



Эти формулы справедливы при условии, когда a/L < 1/5 и А > 0,25, а слой породы, устойчивый пролет которого определяется, не нагружен весом вышележащей голщи пород.

Для слоистой кровли определение пролета камер по методу тонких плит можно свести к расчету балки с эквивалентным пролетом. Такая замена допустима при эквивалентности напряжений и деформаций.