Поддерж. очист. пр-ва целиками. Определение напряжений в нетронутом массиве горных пород при гористом рельефе поверхности
 Скачать 2.58 Mb. Скачать 2.58 Mb.
|
Определение напряжений в нетронутом массиве горных пород при гористом рельефе поверхностиПри подземной разработке рудных месторождений необходимо иметь правильное представление о естественном природном поле напряжений массива пород в районе ведения очистных работ. Особый интерес этот вопрос приобретает тогда, когда месторождение находится в горном районе или разрабатываемая часть месторождения расположена под горным рельефом. Элементы рельефа являются дополнительными источниками напряжений в массиве пород, величина которых зависит от геометрических параметров гор и их расположения относительно месторождения. В горных районах характер распределения напряжений в массиве пород зависит от глубины залегания, горно-геологических структурных особенностей пород, физико-механических свойств пород, а также от тектонической нарушенноети месторождения. Распределением напряжений в массиве пород под горным рельефом занимались многие институты: МГУ, ВНИМИ, ИГД АН Казахстана, ИГД СО АН РФ. СПб Горный университет, Пап. исслед. технолог, университет «МИСиС», ИМиГП Кыргызстана и др. Существующие методы расчета позволяют определять напряжения в условиях изотропной упругой полуплоскости под действием равномерного давления. В аналитических решениях нс рассматриваются размеры зоны влияния горного рельефа, определение которых затруднительно. В работах Н. Г. Ялымова даны зависимости области влияния горного рельефа на массив пород иод основанием горы. Однако в этих зависимостях не учитывают горно-геологические и физико-механические характеристики массива пород под основанием горы и самой горы. С этой целью были определены размеры области влияния горы на нижележащий массив под се основанием. При этом было использовано известное решение о распределении напряжений в полу бесконечном теле под действием равномерного давления, распределенного по полосе конечной ширины (штампа) рисунка 1.19. Такое распределение наг рузки возможно только, когда гора имеет прямоугольную форму высотой /?| и шириной а. При этом равномерное давление определяется как Р = Y'К (У — объемный вес горы). 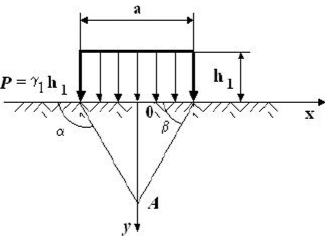 Рис. 1.19. Схема для определения напряжений под действием равномерно распределенной нагрузки 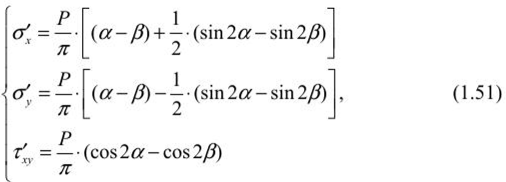 где гГ; гг'; г'. — соответственно горизонтальные (по оси х), вертикальные (по оси х) и тангенциальные напряжения, МПа; Р — нагрузка в любой точке, МПа. В связи с тем, что теоретически влияние рельефа затухает на бесконечности, то для определения его границы принимается критерий: 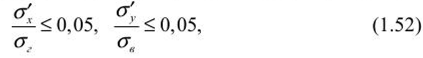 где о;, cs„ — соответственно горизонтальные и вертикальные напряжения, определяемые по гипотезе Гейма— Динника при отсутствии рельефа. Следует отметить, что в работе Н. Г. Ялымова доказано, что распределение напряжений не зависит от формы горы. Поэтому автором учебного пособия были проведены аналитические исследования по установлению распределения напряжений под основанием возвышенности от различной ее формы, а высоту /)/ следует выбирать усредненной следующим образом. Если гора имеет форму треугольника, то высота /?, = hi2 (h — высота горы). В случае, когда гора имеет неправильную форму, приближающуюся к параболическому виду, то h =2/г/3. Поэтому любую форму горы можно свести к виду треугольника либо параболы. Теперь найдем вертикальные напряжения но оси, проходящей через центр прикладываемой нагрузки (ем. рис. 1.19). Очевидно, что в этом месте влияние горного рельефа будет максимальным. Для выявления этого влияния воспользуемся формулами (1.51) и (1.52) для вертикальных составляющих: Из рисунка 1.19 видно, что а= к-р, тогда из формулы (1.51) второе уравнение примет вид 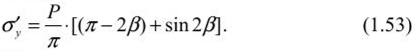 Но из формулы (1.52) имеем: где А - максимальная глубина влияния горы на массив горных пород, расположенный под основанием горы, м. Подставляя это выражение в формулу (1.53) и выразив угол р через а и А, получим уравнение 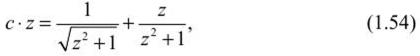 А л у а где z = 2—; с =-----, у — удельный вес горных пород, располо- а 20 у, /?, женных под основанием горы, МН/м . Решая уравнение (1.54) относительно А для горы в виде плоского штампа, находим: 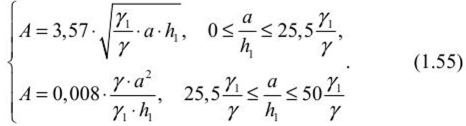 Из формулы (1.55) следует, что максимальная глубина влияния горного рельефа зависит от отношения основания горы к се высоте, а также от отношения удельных весов пород, слагающих, горный массив и массив под основанием горы. ci У У При — = 50— и — = 1, получим А = 20 h, т. е. на этой глубине К У У от основания горы вертикальные напряжения нс превышают 5% относительно веса налегающих пород при отсутствии рельефа. Аналогичное выражение при выбранных параметрах горных пород получено по методике Н. Г. Ялымова. Отличие заключается в том, что не учтены горно-геологические свойства массива горных пород в самой возвышенности и массива под се основанием, а также форма контура возвышенности, что в работах отмстил автор данного а У учебного пособия. При — > 50— следует А принять равным 20/?|. У  Боровков Юрий Александрович (род. 195!)— доктор технических наук (2000), окончил Московский горный институт в 1974 г. по специальности «Физико-технические проблемы горного производства». После окончания вуза работал в проектном институте «Гипроцветмет», а с 1980 г. работает в Российском государственном геологоразведочном университете на кафедре «Геотехнологические способы и физические процессы горного производства» в должности профессора. Он является создателем научного направления в геомеханике — обоснование устойчивых параметров горных выработок с учетом влияния рельефа земной поверхности на напряженно- деформированное состояние подработанного массива горных пород. Ему присвоено почетное звание «Заслуженный деятель науки Российской Федерации» (2004), был избран действительным членом (академиком): Российской Академии Естественных Наук (РАЕН), Международной Академии Наук Экологии и Безопасности жизнедеятельности (МАНЭБ) и Международной (Британской) Академии образования (МАМ). Для горного рельефа треугольного вида глубину влияния горы определим из еистемы уравнений: 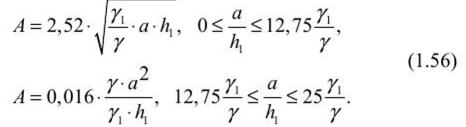 Для гор, имеющих параболическую форму. 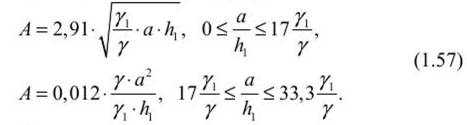 Рассчитав глубину, необходимо определить и ширину зоны влияния горного рельефа от оси, проходящей через центр. Она определяется уравнением эллипса: 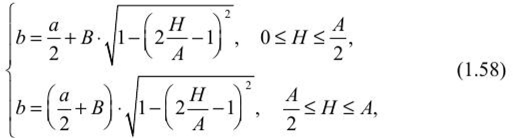 где В = J ^ 2 - т — коэффициент бокового распора. Пользуясь вышеприведенными формулами (1.56)—(1.58), можно определить геометрические размеры зоны влияния горного рельефа. Зная параметры зоны влияния горного рельефа на напряженно- деформированное состояние породного массива под основанием горы, можно в каждой точке этой зоны найти полные напряжения (<7 ), которые будут определяться как: где о — напряжения, обусловленные собственным весом пород до дневной поверхности; o' — напряжения, вызванные влиянием горного рельефа. |
