Роль механики в подготовке будущего инженерамеханика. Основные этапы развития механики
 Скачать 2.42 Mb.
|
0. Но, с другой стороны, система сил (F, F', F") эквивалентна силе F' и паре сил (F, F"); следовательно, сила F эквивалентна силе F' и
Теоретическая механика не только позволяет объяснить ряд важных явлений в окружающем мире, но и служит научным фундаментом для многих технических дисциплин. Ее методами и приемами пользуются при всех технических расчетах, связанных с проектированием различных сооружений и машин и их эксплуатацией. Помимо важного образовательного значения, изучение теоретической механики играет огромную роль в развитии профессионального мышления техника или будущего инженера. Чем лучше и глубже будут усвоены студентами основные положения теоретической механики, тем легче будет для них переход к продуктивному изучению специальных технических дисциплин, необходимых для инженерной деятельности. Курс теоретической механики имеет давнюю историю, он формировался столетиями и традиционная методика его преподавания в большинстве вузов находится на достаточно высоком уровне. Вместе с тем для многих преподавателей высшей технической школы теоретическая механика - предмет традиционный, лишенный новизны и четкой практической значимости в подготовке будущего специалиста-инженера. Обучение строится по испытанной классической схеме изложения материала с последующим закреплением и контролем качества усвоения. Это не позволяет в полной мере рассматривать процесс преподавания теоретической механики как важный фактор профессиональной подготовки современного инженера. Таким образом, учитывая, что фундаментом инженерного образования служат предметы физико-математического цикла, к числу которых относится теоретическая механика, очевидна необходимость выявления психолого-педагогических условий совершенствования преподавания теоретической механики будущим инженерам с целью улучшения их профессиональной подготовки и развития у них профессионально важных качеств. 2.Предмет статики. Основные понятия и определения статики Статикой называется раздел механики, в котором излагается общее учение о силах и изучается условия равновесия материальных тел, находящихся под действием сил. Твердое тело. В статике и вообще в теоретической механике все тела считаются абсолютно твердыми. То есть предполагается, что эти тела не деформируются, не изменяют свою форму и объем, какое бы действие на них не было оказано. Материальной точкой будет называться абсолютно твердое тело, размерами которого можно пренебречь. Исследованием движения нетвердых тел – упругих, пластичных, жидких, газообразных, занимаются другие науки (сопротивление материалов, теория упругости, гидродинамика и т.д.). Под равновесием будем понимать состояния покоя тела по отношению к другим материальным телам. Основные понятия: 1. Величина, являющаяся количественной мерой механического взаимодействия материальных тел, называется в механике силой. В Международной системе единиц (СИ) силу измеряют в ньютонах (Н), килоньютонах (кН). Сила является величиной векторной. Основные понятия: Про тело говорят, что оно находится в равновесии, если оно покоится или движется равномерно и прямолинейно относительно выбранной инерциальной системы отсчёта. В статике материальные тела считают абсолютно твёрдыми, т.к. изменение размеров тел обычно мало по сравнению с начальными размерами. Связи На тело влияют внешние силы, а также другие материальные тела, ограничивающие перемещение данного тела в пространстве. Такие тела называют связями. Сила, с которой связь действует на тело, ограничивая его перемещение, называется реакцией связи. Для записи условия равновесия системы связи убирают, а реакции связей заменяют на равные им силы. Например, если тело закреплено на шарнире, то шарнир является связью. Реакцией связи, при этом будет сила, проходящая через ось шарнира.. Системы сил Если систему сил, действующих на твёрдое тело, можно заменить на другую систему сил, не изменяя механического состояния тела, то такие системы сил называются эквивалентными. Для любой системы сил, приложенных к твёрдому телу, можно найти эквивалентную систему сил, состоящую из силы, приложенной в заданной точке (центре приведения), и пары сил. Эта сила называется главным вектором системы сил, а момент, создаваемый парой сил — главным моментом относительно выбранного центра приведения. Главный вектор равен векторной сумме всех сил системы и не зависит от выбранного центра приведения. Главный момент равен сумме моментов всех сил системы относительно центра приведения. Совокупность сил, действующих на какое-нибудь твердое тело, будем называть системой сил Тело, не скрепленное с другими телами, которому из данного положения можно сообщить любое перемещение в пространстве, называется свободным. Если одну систему сил, действующих на свободное твердое тело, можно заменить другой системой, не изменяя при этом состояния покоя или движения, в котором находится тело, то такие две системы сил называются эквивалентными. Система сил, под действием которой свободное твердое тело может находиться в покое, называется уравновешенной или эквивалентной нулю. Если данная система сил эквивалентна одной силе, то эта сила называется равнодействующей данной системы сил. Сила, равная равнодействующей по модулю, прямо противоположная ей по направлению и действующая вдоль той же прямой, называется уравновешивающей силой. Сила, приложенная к телу в какой-нибудь одной его точке, называется сосредоточенной. Вопрос№.3.Аксиомы статики Аксиомы статики. Все теоремы и уравнения статики выводятся из нескольких исходных положений, принимаемых без математических доказательств и называемых аксиомами или принципами статики. Аксиомы статики представляют собою результат обобщений многочисленных опытов и наблюдений над равновесием и движением тел, неоднократно подтвержденных практикой. Часть из этих аксиом является следствиями основных законов механики, с которыми мы познакомимся в динамике. Аксиома 1. Если на свободное абсолютно твердое тело действуют две силы, то тело может находиться в равновесии тогда и только тогда, когда эти силы равны по модулю (F1 = F2) и направлены вдоль одной прямой в противоположные стороны Аксиома1 определяет простейшую уравновешенную систему сил, так как опыт показывает, что свободное тело, на которое действует только одна сила, находиться в равновесии не может. Аксиома2. Действие данной системы, сил на абсолютно твердое тело не изменится, если к ней прибавить или от нее отнять уравновешенную систему сил. Эта аксиома устанавливает, что две системы сил, отличающиеся на уравновешенную систему, эквивалентны друг другу. Следствие из 1-й и 2-й аксиом. Действие силы на абсолютно твердое тело не изменится, если перенести точку приложения силы вдоль ее линии действия в любую другую точку тела. Аксиома 3 (аксиома параллелограмма сил). Две силы, приложенные к телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю параллелограмма, построенного на этих силах, как на сторонах. Аксиома4 (принцип противодействия). При всяком действии одного материального тела на другое имеет место такое же по величине, но противоположное по направлению противодействие. Закон о равенстве действия и противодействия является одним из основных законов механики Аксиома 5 (принцип отвердевания). Равновесие изменяемого (деформируемого) тела, находящегося под действием данной системы сил, не нарушится, если тело считать отвердевшим (абсолютно твердым). Из принципа отвердения следует, что условия, необходимые и достаточные для равновесия абсолютно твердого тела, необходимы, но не достаточны для равновесия деформируемого тела, по форме и размерам тождественного с данным. Высказанное в этой аксиоме утверждение очевидно. Например, ясно, что равновесие цепи не нарушится, если ее звенья считать сваренными друг с другом и т. д. Аксиома 6 (аксиома связей).Всякое несвободное тело можно рассматривать как свободное, если механическое действие связей заменить реакциями этих связей (пояснения к этой аксиоме в следующем параграфе). Приведенные принципы и аксиомы положены в основу методов решения задач статики. Все они широко используются в инженерных расчетах. Аксиома 1 Аксиома 2 Аксиома3 Аксиома 4     Вопрос№4. Связи и их реакции. Аксиома связей. Тема 2. Связи и их реакции Тело, которое может совершать из данного положения любые перемещения в пространстве, называется свободным. Тело, перемещениям которого препятствуют какие-нибудь другие, скрепленные или соприкасающиеся с ним тела, называется несвободным. Все то, что ограничивает перемещение данного тела, называют связью. Сила, с которой данная связь действует на тело, препятствующая тем или иным его перемещениям, называется реакцией связи. Реакция связи направлена в сторону противоположную той, куда связь не дает перемещаться телу. Принцип освобождаемости от связей: несвободное твердое тело можно рассматривать как свободное, если его мысленно освободить от связей, заменив их действие реакциями. В статике этот принцип позволяет рассматривать равновесие несвободного твердого тела как свободного под действием активных (заданных) сил и реакций связей. Рассмотрим наиболее часто встречающиеся типы связей на плоскости и направления их реакций. 1. Гладкая плоскость (поверхность) или опора Реакция N гладкой плоскости (поверхности) или опоры направлена по общей нормали к поверхностям соприкасающихся тел в точке их касания и приложена к этой точке. 2. Гибкая нить (провода, канаты, цепи, ремни) Реакция Т направлена вдоль нити к точке подвеса. 3. Невесомый стержень с шарнирами Реакция N невесомого стержня направлена вдоль стержня. Обычно реакция Nизображается от тела по стержню, в предположении, что в равновесии стержень растянут. 4. Неподвижный цилиндрический шарнир илиподшипник Реакция RA цилиндрического шарнира может иметь любое направление в плоскости, перпендикулярной оси вращения, т. е. в плоскости Аху. Обычно ее раскладывают на две составляющие ХА и YA по двум взаимноперпендикулярным направлениям. 5. Шарнирно-подвижная опора (опора на катках) Реакция R проходит через ось шарнира и направлена перпендикулярно к опорной плоскости. 6. Жесткая заделка Нахождение реакции жесткой заделки сводится к определению составляющих ХА и YA препятствующих линейному перемещению балки в плоскости действия сил, и алгебраической величине момента mA, препятствующего вращению балки под действием приложенных к ней сил. Аксиома связей (принцип освобождения от связей) — одна из аксиом теоретической механики. Может быть сформулирована следующим образом: Всякое несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их действие реакциями этих связей. При этом под связью понимается всё то, что ограничивает движение тела. Простейший пример применения аксиомы связей: если на горизонтальной поверхности (например, на столе) в поле тяжести Земли (то есть, в "обычных" земных условиях) лежит тело, то мы можем мысленно отбросить горизонтальную поверхность и заменить её действие силой реакции этой поверхности. 5. План решения задач(Рассмотреть на примере) Приступая к решению задания, необходимо разобраться в условии задачи и рисунке, а затем: 1. Составить расчетную схему, которая включает: - объект равновесия, - активные (заданные) силы, - силы реакции, заменяющие действия отброшенных связей. 2. Определить вид полученной системы сил и выбрать, соответствующие ей, уравнения равновесия; 3. Выяснить, является ли задача статически определимой; 4. Составить уравнения равновесия и определить из них силы реакции; 5. Сделать проверку полученных результатов. При замене связей (опор) силами реакций помнить: - если связь препятствует перемещению тела только в одном каком-нибудь направлении, то направление ее реакции противоположно этому направлению; - если же связь препятствует перемещению тела по многим направлениям, то силу реакции такой связи изображают ее составляющими, показывая их параллельно выбранным координатным осям и . Решение уравнений равновесия будет тем проще, чем меньшее число неизвестных будет входить в каждое из них. Поэтому, при составлении уравнений равновесия следует: 1) координатные оси и располагать так, чтобы одна из осей была перпендикулярна к линии действия хотя бы одной из неизвестных сил, в этом случае проекция неизвестной силы исключается из соответствующего уравнения равновесия; 2) за центр моментов выбирать точку, в которой пересекаются линии действия наибольшего числа неизвестных сил реакций, тогда моменты этих сил не войдут в уравнение моментов. Если сила в плоскости имеет две составляющие ее силы и , то при вычислении момента силы вокруг некоторой точки О, полезно применить теорему Вариньона, вычислив сумму моментов составляющих ее сил относительно этой точки (см. рис. 4). Если к телу в числе других сил приложена пара сил, то ее действие учитывается только в уравнении моментов сил, куда вносится момент этой пары, с соответствующим, знаком. Пример 1. Шар веса опирается в точке на наклонную плоскость, образующую с вертикалью угол , и привязан к стене веревкой, которая образует с вертикалью угол (рис.13а). Определить реакцию плоскости в точке и натяжение веревки.  Рис.13 Решение: Обозначим искомую реакцию плоскости, направленную по нормали к этой плоскости, через , а натяжение веревки – через . Линия действия всех трех сил и пересекаются в центре шара . Примем вертикаль и горизонталь в точке за координатные оси и найдем проекции сил и на эти оси: , , , , , . Так как данная система сходящихся сил является плоской, то условия равновесия (4) имеют вид 1) 2) Умножив первое уравнение на , а второе на и сложив их, получим . Затем из первого уравнения находим . В случае, когда веревка, удерживающая шар, параллельна наклонной плоскости , получим , . Для решения этой же задачи графическим способом, необходимо построить замкнутый силовой многоугольник. Построение силового многоугольника всегда нужно начинать с известных, заданных сил. Из произвольной точки (рис.13б) проведем вектор , параллельный данной силе , длина которого в выбранном масштабе изображает модуль этой силы. Затем через точки и проводим прямые, параллельные линиям действия искомых сил и , которые пересекутся в точке . Векторы и определяют искомые силы и .Чтобы найти направление искомых сил на силовом треугольнике , нужно обойти этот треугольник по его периметру, причем направление этого обхода определяется направлением данной силы . Измерив длину сторон и и зная масштаб, в котором построена сила , найдем численные значения сил и . 6. Равнодействующая системы сходящихся сил. Геометрический и аналитический способы определения равнодействующей. Равнодействующая системы сходящихся сил - сила, оказывающая на твёрдое тело такое же механическое действие, как и данная система приложенных ктелу сил. В простейших случаях (например, для сил, приложенных в одной точке или расположенных в однойплоскости) равнодействующую можно найти, последовательно применяя закон параллелограмма сил.Равнодействующую имеет не всякая система сил, например, пара сил или две силы, не лежащие в одной плоскости, равнодействующей не имеют. Определение равнодействующей системы сил аналитическим способом Величина равнодействующей равна векторной (геометрической) сумме векторов системы сил. Определяем равнодействующую геометрическим способом. Выберем систему координат, определим проекции всех заданных векторов на эти оси (рис. 3.4а). Складываем проекции всех векторов на оси х и у (рис. 3.46). 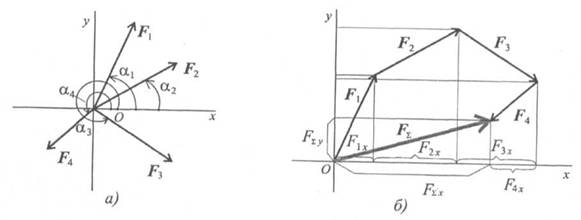 Рис.3.4 FΣч = Flx + F2x + F3x + F4x; FΣн = Fly + F2y + F3y + F4y; ; . Модуль (величину) равнодействующей можно найти по известным проекциям: . Направление вектора равнодействующей можно определить по величинам и знакам косинусов углов, образуемых равнодействующей с осями координат (рис. 3.5). Растяжение сжатие Продольные силы и определение напряжений.
Условия равновесия плоской системы сходящихся сил в аналитической форме. Исходя из того, что равнодействующая равна нулю, получим:  FΣ = 0. Условия равновесия в аналитической форме можно сформулировать следующим образом: Плоская система сходящихся сил находится в равновесии, если алгебраическая сумма проекций всех сил системы на любую ось равна нулю. Система уравнений равновесия плоской сходящейся системы сил:. 7. Условие равновесия системы сходящихся сил в аналитической и геометрической формах Равновесие системы сходящихся сил. Из законов механики следует, что твердое тело, на которое действуют взаимно уравновешенные внешние силы, может не только находиться в покое, но и совершать движение, которое мы назовем движением «по инерции». Таким движением будет, например, поступательное равномерное и прямолинейное движение тела. Отсюда получаем два важных вывода: 1) Условиям равновесия статики удовлетворяют силы, действующие как на покоящееся тело, так и на тело, движущееся «по инерции». 2) Уравновешенность сил, приложенных к свободному твердому телу, является необходимым, но не достаточным условием равновесия (покоя) самого тела; в покое тело будет при этом находиться лишь в том случае, если оно было в покое и до момента приложения к нему уравновешенных сил. Для равновесия приложенной к твердому телу системы сходящихся сил необходимо и достаточно, чтобы равнодействующая этих сил была равна нулю. Условия, которым при этом должны удовлетворять сами силы, можно выразить в геометрической или аналитической форме. 1. Геометрическое условие равновесия. Так как равнодействующая сходящихся сил определяется как замыкающая сторона силового многоугольника, построенного из этих сил, то может обратиться в нуль тогда и только тогда, когда конец последней силы в многоугольнике совпадает с началом первой,т. е. когда многоугольник замкнется. Следовательно, для равновесия системы, сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнут. 2. Аналитические условия равновесия. Аналитически равнодействующая системы сходящихся сил определяется формулой  .Так как под корнем стоит сумма положительных слагаемых, то R обратится в нуль только тогда, когда одновременно  , т. е. когда действующие на тело силы будут удовлетворять равенствам: Равенства выражают условия равновесия в аналитической форме: для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из трех координатных осей были равны нулю. Если все действующие на тело сходящиеся силы лежат в одной плоскости, то они образуют плоскую систему сходящихся сил. В случае плоской системы сходящихся сил получим, очевидно, только два условия равновесия  Равенства выражают также необходимые условия (или уравнения) равновесия свободного твердого тела, находящегося под действием сходящихся сил. Теорема о трех силах. Уравновешенная плоская система трех непараллельных сил является сходящейся. Условие «плоская» в формулировке теоремы не является необходимым можно убедиться, что любая уравновешенная система трех сил всегда будет плоской. Это следует из условий равновесия произвольной пространственной системы сил, которые будут рассмотрены далее. 8. Теорема о трех непараллельных силах Теорема о трёх силах — теорема статики, формулирующая необходимое условие равновесия абсолютно твёрдого тела под действием трёх непараллельных сил. Формулировка теоремы следующая[1][2]: Если абсолютно твердое тело находится в равновесии под действием плоской системы трех непараллельных сил, то линии их действия пересекаются в одной точке. Под тремя непараллельными силами в данном случае понимаются три силы, как минимум две из которых непараллельны. Теорема даёт только необходимое условие равновесия тела Чтобы условие стало достаточным, к нему необходимо прибавить требование равенства нулю геометрической суммы всех трёх сил. Доказательство П  усть тело находится в равновесии под действием сил F1, F2 и F3, точки приложения которых соответственно A, B и C (рис. 1). Положим для определённости, что силы F1 и F2 непараллельны. Следовательно, линии их действия пересекаются в некоторой точке O. Перенесём обе силы вдоль линий их действия в точку O и найдём равнодействующую этих сил F4. Указанные операции не изменят состояния равновесия тела, следовательно, тело теперь будет находиться в равновесии под действием двух сил: F3 иF4. Но тело находится в равновесии под действием двух сил только в том случае, если эти силы направлены по одной линии. Следовательно, линия действия силы F3 также проходит через точку O. Теорема доказана[1].9. Сложение 2-х параллельных сил. Параллельными называют силы, линии, действия которых образуют параллельные прямые. Система сил, линии, действия которых параллельны и лежат в одной плоскости, называется плоской системой параллельных сил. Параллельные силы могут действовать в одном или противоположных направлениях. Сложить такие силы по правилу параллелограмма нельзя, так как они не имеют общей точки приложения. Однако это можно сделать, приняв способ приложения уравновешивающих сил Равнодействующая двух параллельных сил, направленных в одну сторону, равна по модулю сумме модулей данных сил и направлена в ту же сторону. Линия действия равнодействующей делит внутренним образом расстояние между линиями действия данных сил на части, обратно пропорциональные этим силам. 10. Пара сил. Векторный момент пары. Алгебраический момент пары. Па́ра сил — совокупность двух сил, которые приложены к одному абсолютно твёрдому телу и при этом равны по модулю и противоположны по направлению. Пара сил представляет собой важный частный случай системы сил. Главным вектором для неё служит нулевой вектор, так что действие пары сил на тело полностью характеризуется её главным моментом, который является свободным вектором (не зависит от выбора полюса) и называется моментом пары сил. В соответствии с этим, момент пары сил не имеет точки приложения (утверждение, иногда называемое «второй теоремой Вариньона»): к каким бы частям твёрдого тела ни прикладывались силы, составляющие пару, при данных модуле и направлении момента пары двигаться оно будет одинаково. Кратчайшее расстояние между линиями действия сил, образующих пару, называют плечом пары. Модуль момента пары сил равен произведению модуля одной из сил на плечо: . Как и любой механический момент, момент пары сил является псевдовекторной величиной; он направлен перпендикулярно плоскости, задаваемой линиями действия сил:  (при этом направление вектора плеча условно следует задавать в сторону к точке приложения выбранной из пары силы ).Пара сил, момент которой отличен от нуля — простейший пример системы сил, не имеющей равнодействующей. Действие силы, приложенной к твёрдому телу на некотором расстоянии d от центра масс (в точке, в которую из центра масс можно провести вектор ), эквивалентно действию такой же силы, приложенной непосредственно к центру масс, комбинированной с некоторой парой сил, такой, что  , то есть с моментом, равным моменту силы относительно центра масс (в частности, если , можем задаться , в таком случае одна из сил будет приложена в той же точке, что и исходная, и составит ).11. Эквивалентность пар. Теорема об эквивалентности пар. Две пары сил считаются эквивалентными в том случае, если после замены одной пары другой парой механическое состояние тела не изменяется, т. е. не изменяется движение тела или не нарушается его равновесие. Эффект действия пары сил на твердое тело не зависит от ее положения в плоскости. Таким образом, пару сил можно переносить в плоскости ее действия в любое положение. Существует две теоремы об эквивалентности пар: Теорема 1. ( Об эквивалентности пар на плоскости ). Две пары, лежащие в одной плоскости и имеющие равные по величине и по знаку моменты, эквивалентны. Теорема 2. ( Об эквивалентности пар в пространстве ). Две пары, лежащие в параллельных плоскостях и имеющие равные по величине и по знаку моменты, эквивалентны. Вопрос 12 Докажем лемму: Сила, приложенная в какой-либо точке твердого тела, эквивалентна такой же силе, приложенной в любой другой точке этого тела, и паре сил, момент которой равен моменту данной силы относительно новой точки приложения. Пусть в точке А твердого тела приложена сила F Приложим теперь в точке В тела систему двух сил F' и F²-, эквивалентную нулю, причем выбираем F'=F (следовательно, F"=–F). Тогда сила F |
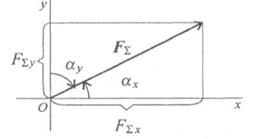
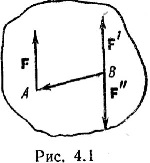паре сил (F, F"). Момент пары (F, F") равен M=M(F,F")=BAxF, т.е. равен моменту силы F относительно точки В M=MB(F). Таким образом, лемма о параллельном переносе силы доказана.