Роль механики в подготовке будущего инженерамеханика. Основные этапы развития механики
 Скачать 2.42 Mb. Скачать 2.42 Mb.
|
|
34 Центром тяжести твердого тела называется геометрическая точка, жестко связанная с этим телом, и являющаяся центром параллельных сил тяжести, приложенных к отдельным элементарным частицам тела (рисунок 1.6). Радиус-вектор этой точки 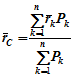 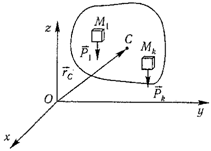 Рисунок 1.6 Для однородного тела положение центра тяжести тела не зависит от материала, а определяется геометрической формой тела. Если удельный вес однородного тела γ, вес элементарной частицы тела Pk= γΔVk (P = γV) подставить в формулу для определения rC, имеем 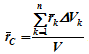 Откуда, проецируя на оси и переходя к пределу, получаем координаты центра тяжести однородного объема 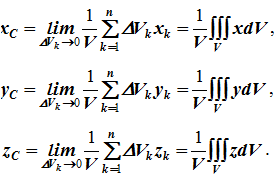 Аналогично для координат центра тяжести однородной поверхности площадью S (рисунок 1.7, а) 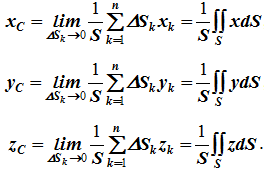 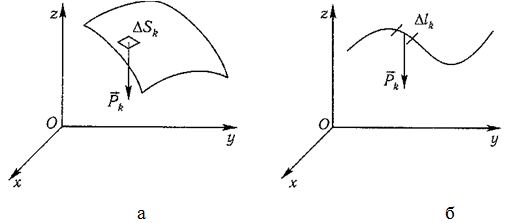 Рисунок 1.7 Для координат центра тяжести однородной линии длиной L (рисунок 1.7, б) 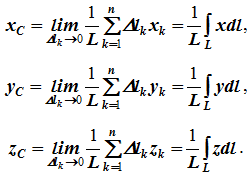 35На каждую частицу тела, находящегося вблизи поверхности Земли, действует направленная вертикально вниз сила, которая называется силой тяжести. Силы тяжести каждой частицы тела, строго говоря, направлены по радиусам к центру Земли и не являются параллельными. Но для тел, размеры которых малы по сравнению с размерами Земли, непараллельность настолько незначительна, что в расчетах с большой точностью силы тяжести их частиц можно считать параллельными, сохраняющими свои значения, точки приложения и параллельность при любых поворотах тела. Поэтому, обозначив силу тяжести частицы через Рк , можно, согласно формулам 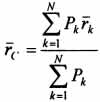 и и 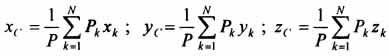 , найти точку С, которая неизменно связана с телом и называется центром системы параллельных сил тяжести. Таким образом, центром тяжести твердого тела называется центр системы параллельных сил тяжести частиц данного тела. Точка С — это геометрическая точка, она может и не принадлежать телу, но она всегда с ним связана, например центр тяжести баскетбольного мяча, кольца и др. Выразим силу тяжести (вес) частицы тела через ее объем V. Тогда величина , найти точку С, которая неизменно связана с телом и называется центром системы параллельных сил тяжести. Таким образом, центром тяжести твердого тела называется центр системы параллельных сил тяжести частиц данного тела. Точка С — это геометрическая точка, она может и не принадлежать телу, но она всегда с ним связана, например центр тяжести баскетбольного мяча, кольца и др. Выразим силу тяжести (вес) частицы тела через ее объем V. Тогда величина Методы нахождения центра тяжести. 1) Метод симметрии. Покажем, что если однородное тело имеет плоскость, ось или центр материальной симметрии, то его центр тяжести находится соответственно в плоскости, на оси или в центре симметрии. а. Пусть тело симметрично относительно плоскости Оху 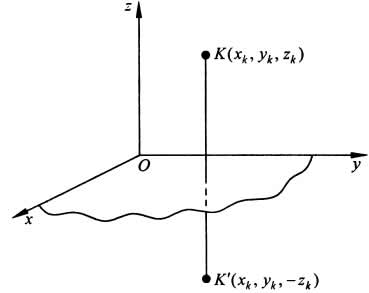 Тогда вследствие симметрии каждому элементу К тела объемом 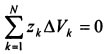 и координата и координата 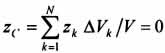 . Следовательно, центр тяжести тела будет лежать в плоскости симметрии Оху. . Следовательно, центр тяжести тела будет лежать в плоскости симметрии Оху.б. Пусть тело симметрично относительно оси Oz. 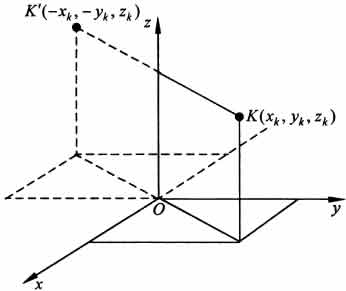 Тогда всякому элементу К тела объемом 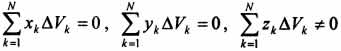 и, следовательно, координаты и, следовательно, координаты 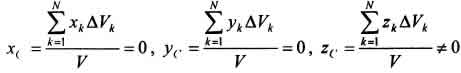 . Таким образом, центр тяжести будет находится на оси симметрии. . Таким образом, центр тяжести будет находится на оси симметрии.в. Пусть тело имеет центр симметрии, который примем за начало координат. Тогда всякой частице тела объемом или круглой пластины лежат в геометрическом центре этих тел. 2) Метод разбиения. Этот метод основан на применении формул 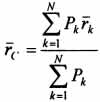 и и 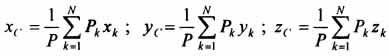 . Его используют, когда тело можно разбить на ряд частей, центры тяжести которых известны из условий симметрии. Метод разбиения можно наглядно проиллюстрировать с помощью рисунка. . Его используют, когда тело можно разбить на ряд частей, центры тяжести которых известны из условий симметрии. Метод разбиения можно наглядно проиллюстрировать с помощью рисунка.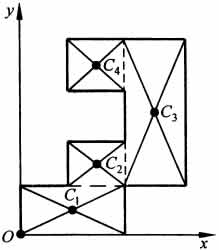 Расположив тело в системе координат, разделив его мысленно на отдельные части, веса которых Р1, Р2, Р3, Р4, а центры тяжести известны, вычислим вес тела и, согласно формулам 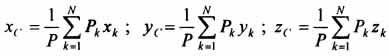 , координаты центра тяжести С всего тела. Если тело имеет вырез, причем известны центр тяжести тела без выреза и центр тяжести вырезанного тела, то для определения координат центра тяжести используют метод отрицательных масс (частный случай метода разбиения). , координаты центра тяжести С всего тела. Если тело имеет вырез, причем известны центр тяжести тела без выреза и центр тяжести вырезанного тела, то для определения координат центра тяжести используют метод отрицательных масс (частный случай метода разбиения).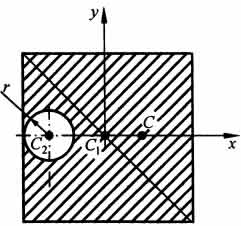 На рисунке изображена квадратная пластина, сторона которой а. В пластине выполнено круглое отверстие с радиусом r=0,2а и координатами центра x2=-0,3а; у2=0. Координаты центра тяжести С, пластины без отверстия x1=0, у1=0. Рассмотрим два тела: пластину без отверстия и диск, соответствующий вырезанному отверстию. При использовании формул 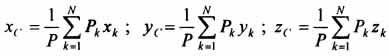 вес диска будем считать отрицательным. Тогда вес диска будем считать отрицательным. Тогда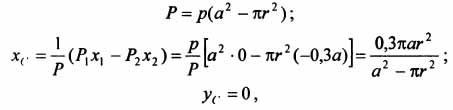 , где р — вес единицы площади пластины. , где р — вес единицы площади пластины.36. Центр тяжести дуги окружности, кругового сектора, полукруга. Центр тяжести дуги окружности 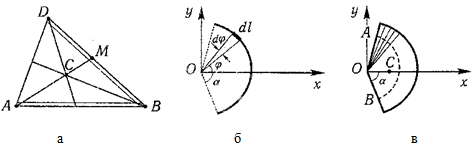 Дуга имеет ось симметрии. Центр тяжести лежит на этой оси, т.е. yC = 0. 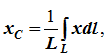 dl – элемент дуги, dl = Rdφ, R – радиус окружности, x = Rcosφ, L = 2αR, 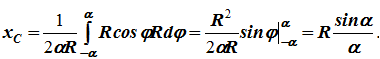 Следовательно: xC = R(sinα/α). Центр тяжести кругового сектора  Сектор радиуса R с центральным углом 2α имеет ось симметрии Ox, на которой находится центр тяжести. Разбиваем сектор на элементарные секторы, которые можно считать треугольниками. Центры тяжести элементарных секторов располагаются на дуге окружности радиуса (2/3)R. Центр тяжести сектора совпадает с центром тяжести дуги AB: 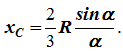 Полукруг: 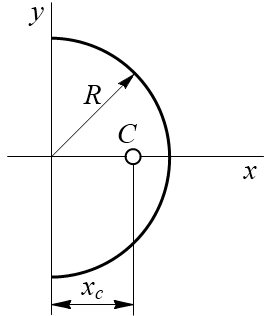 37. Кинематика. Кинематика точки. Способы задания движения точки. Кинематика – раздел механики, в котором изучаются движение материальных тел с геометрической точки зрения, без учета массы и действующих на них сил. Способы задания движения точки: 1) естественный, 2) координатный, 3) векторный. Кинема́тика точки — раздел кинематики, изучающий математическое описание движения материпльных точек. Основной задачей кинематики является описание движения при помощи математического аппарата без выяснения причин, вызывающих это движение. Естественный сп. указывается траектория точки, закон ее движения по этой траектории, начало и направление отсчета дуговой координаты: s=f(t) – закон движения точки. При прямолинейном движении: х=f(t). Координатный сп. положение точки в пространстве определяется тремя координатами, изменения которых определяют закон движения точки: x=f1(t), y=f2(t), z=f3(t). Если движение в плоскости, то два уравнения движения. Уравнения движения описывают уравнение траектории в параметрической форме. Исключив из уравнений параметр t, получаем уравнение траектории в обычном виде:f(x,y)=0 (для плоск-ти). Векторный сп. положение точки определяется ее радиус-вектором , проведенным из какого-либо центра. Кривая, которая вычерчивается концом какого-либо вектора, назыв. годографом этого вектора. Т.е. траектория – годограф радиус-вектора. 38.Связь между координатным и векторным, координатным и естественным способами задания движения точки. СВЯЗЬ ВЕКТОРНОГО СПОСОБА С КООРДИНАТНЫМ И ЕСТЕСТВЕННЫМ выражается соотношениями: 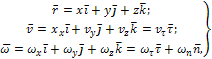 где - орт касательной к траектории в данной точке, направленный в сторону отсчета расстояний, - орт нормали к траектории в данной точке, направленный в сторону центра кривизны (см. рис. 3). СВЯЗЬ КООРДИНАТНОГО СПОСОБА С ЕСТЕСТВЕННЫМ. Уравнение траектории f(x, y)=z; f1(x, z)=y получается из уравнений движения в координатной форме посредством исключения времени t. Дополнительным анализом значений, которые могут принимать координаты точки, определяется тот участок кривой 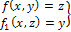 , который является траекторией. Например, если движение точки задано уравнениями: x=sin t; y=sin2t=x2, то траекторией точки является тот участок параболы у=х2, для которого -1≤x≤+1, 0≤x≤1. Начало и направление отсчета расстояний выбираются произвольно, этим в дальнейшем определяется знак скорости и величина и знак начального расстояния s0. , который является траекторией. Например, если движение точки задано уравнениями: x=sin t; y=sin2t=x2, то траекторией точки является тот участок параболы у=х2, для которого -1≤x≤+1, 0≤x≤1. Начало и направление отсчета расстояний выбираются произвольно, этим в дальнейшем определяется знак скорости и величина и знак начального расстояния s0.Закон движения определяется зависимостью: 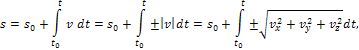 знак + или - определяется в зависимости от принятого направления отсчета расстояний. 39 Скорость точки – это кинематическая мера ее движения, равная производной по времени от радиус-вектора этой точки в рассматриваемой системе отсчета. Вектор скорости направлен по касательной к траектории точки в сторону движения Вектор скорости (v) — это расстояние, которое тело проходит в определенном направлении за единицу времени. Обратите внимание, что определение вектора скорости очень похоже на определение скорости, за исключением одного важного различия: скорость тела не указывает направление движения, а вектор скорости тела указывает и скорость, и направление движения. Следовательно, необходимы две переменные, которые описывают вектор скорости тела: скорость и направление. Физические величины, у которых есть значение и направление, называют векторными величинами. Вектор скорости тела может время от времени изменяться. Если или его скорость, или направление изменяются, скорость тела также меняется. Постоянный вектор скорости подразумевает неизменную скорость и неизменное направление, тогда как термин «постоянная скорость» подразумевает только неизменное значение, не принимая во внимание направление. Термин «вектор скорости» часто используется попеременно с термином «скорость». Они оба выражают расстояние, которое тело проходит в единицу времени 40 Ускорение точки – это мера изменения ее скорости, равная производной по времени от скорости этой точки или второй производной от радиус-вектора точки по времени. Ускорение характеризует изменение вектора скорости по величине и направлению и направлено в сторону вогнутости траектории. Вектор ускорения это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой: где Направление вектора ускорения совпадает с направлением изменения скорости Δ В момент времени t1 (см. рис 1.8) тело имеет скорость 41 1.4 Определение скорости и ускорения точки при координатном способе задания движения Связь векторного способа задания движения и координатного дается соотношением Из определения скорости 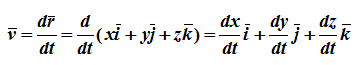 Проекции скорости на оси координат равны производным соответствующих координат по времени: Модуль и направление скорости определяются выражениями 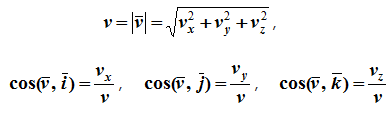 Из определения ускорения 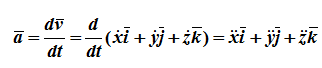 Проекции ускорения на оси координат равны вторым производным соответствующих координат по времени Модуль и направление ускорения определяются выражениями 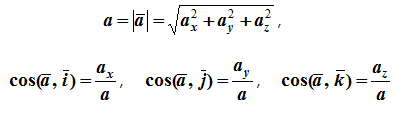 42 Определение скорости и ускорения точки при естественном способе задания движения Скорость точки.Вектор скорости точки всегда направлен по касательной вдоль оси числовая величина скорости точки в данный момент времени равна первой производной от расстояния (криволинейной координаты) Следовательно, численная величина скорости определяет одновременно и модуль вектора скорости и сторону, в которую он направлен. 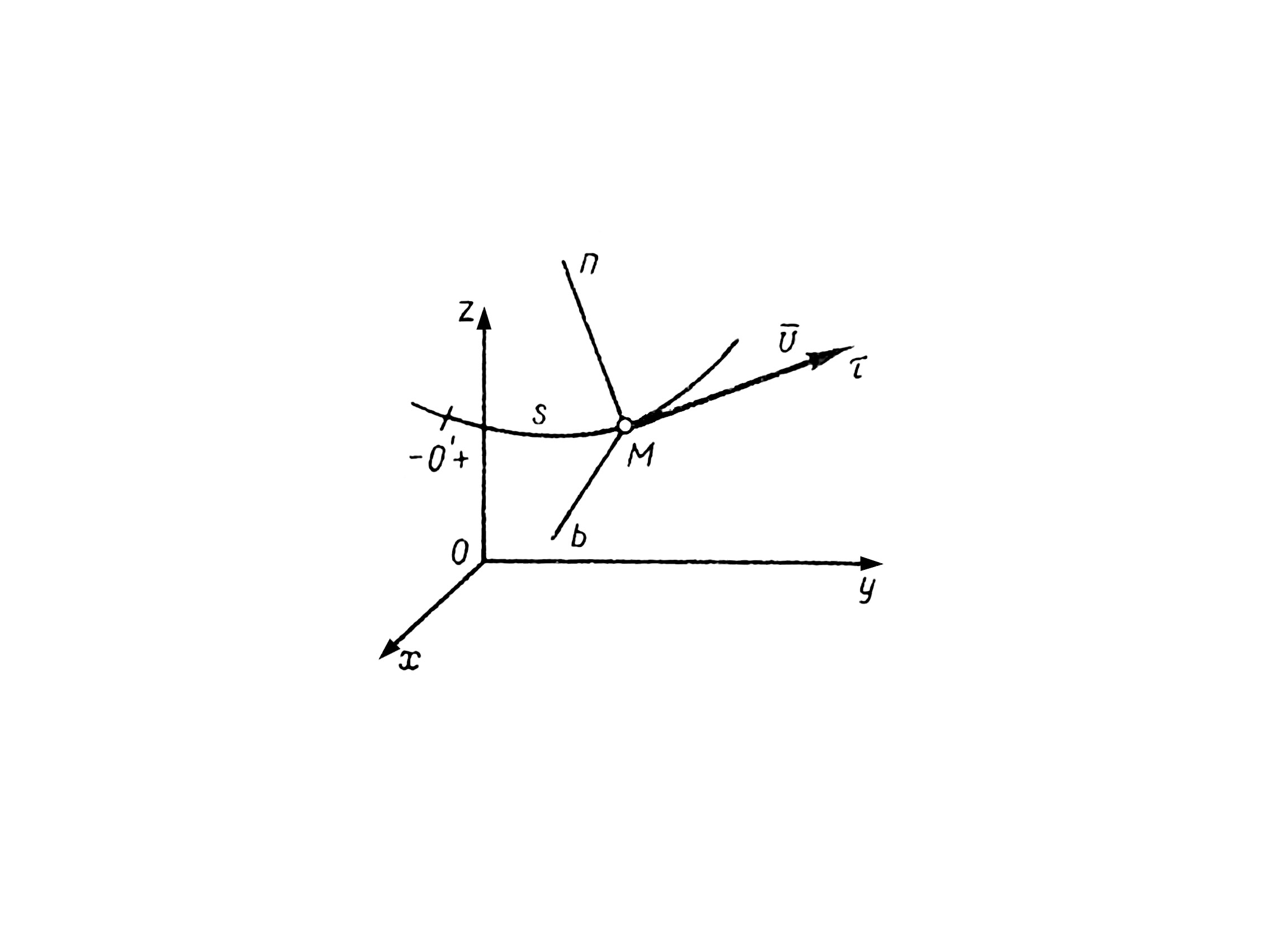 Касательное и нормальное ускорения точки. При естественном способе задания движения вектор ускорения определяют по его проекции на оси Проекции ускорения на оси где - радиус кривизны траектории. Проекция ускорения точки на касательную равна первой производной от численной величины скорости или второй производной от расстояния (криволинейной координаты) Если заданы проекции скорости 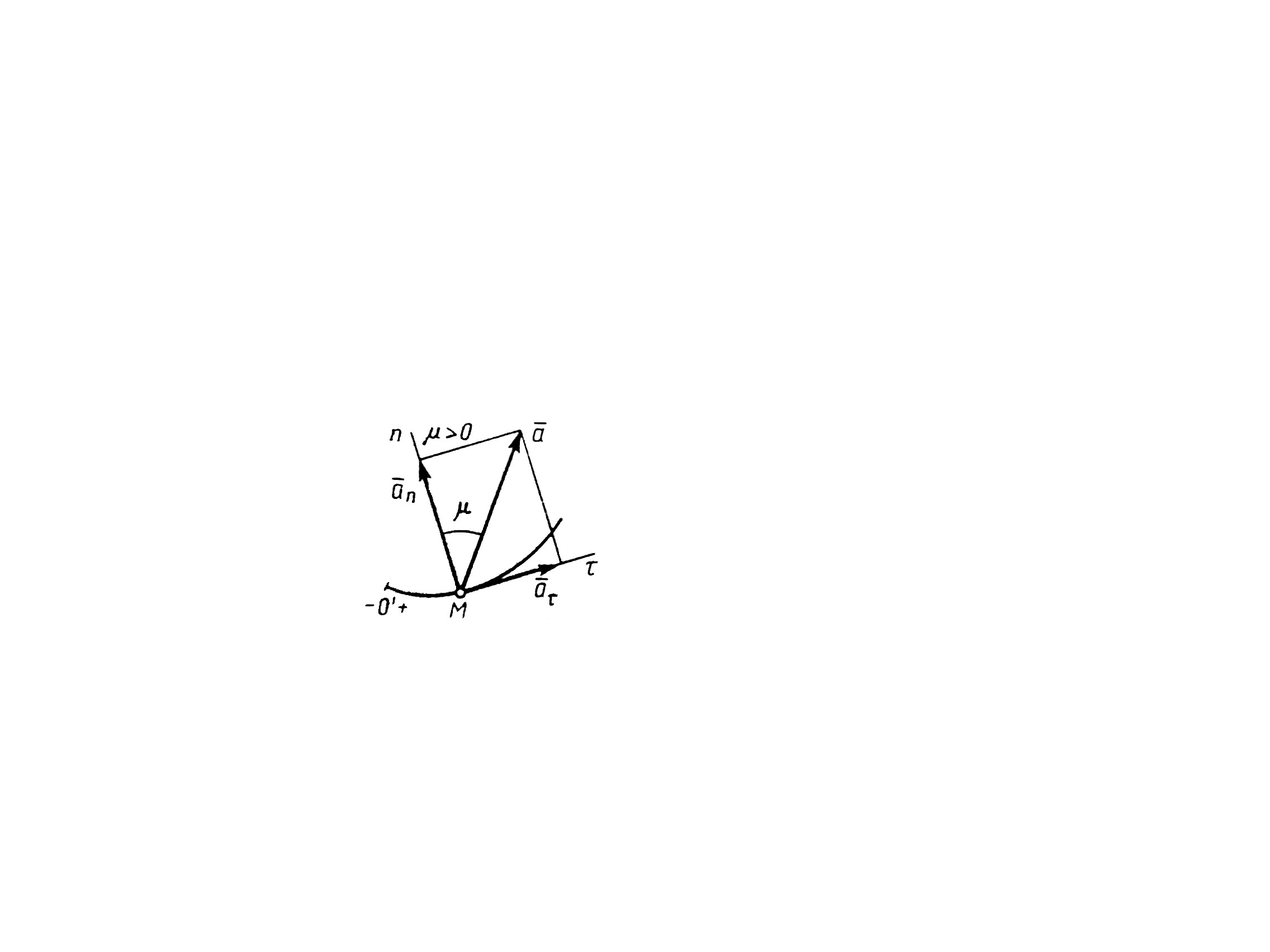 Вектор ускорения точки Вектор ускорения точки 43 кинемотика твердого тела .виды движения твердых тел.поступательное движения твердого тела. во многих случаях деформации твердых тел столь незначительны, что ими можно пренебречь при исследовании движения и равновесия твердых тел и рассматривать эти тела как недеформируемые (или абсолютно твердые)Абсолютно твердым телом называют такое твердое тело, расстояние между двумя любыми точками которого остается неизменным. Теоретическая механика изучает движение и равновесие только абсолютно твердых тел, и для краткости их называют просто твердыми телами .Задачи кинематики твердого тела разделяются на 2 части:1. Задачи движения и изучения кинематических характеристик движения всего тела в целом.2. Изучение движения каждой из точек тела в отдельности.Твердое тело может совершать пять видов движения: поступательное, вращение вокруг неподвижной оси, плоскопараллельное, вращение вокруг неподвижной точки и свободное.Поступательное движение твердого тела – это движение, при котором любая прямая, связанная с телом, при его движении остается параллельной своему начальному положению.Примеры поступательного движения: движение педалей велосипеда относительно его рамы, движение поршней в цилиндрах двигателя внутреннего сгорания относительно цилиндров, движение кабин колеса обозрения относительно Земли (рисунок 1.1) и т.д.  Рис. 1.1 Рис. 1.1Теорема. При поступательном движении твердого тела траектории, скорости и ускорения точек тела одинаковы.Доказательство. Если выбрать две точки твердого тела А и В (рисунок 1.2), то радиусы-векторы этих точек связаны соотношением Траектория точки А – это кривая, которая задается функцией rA(t), а траектория точкиB – это кривая, которая задается функцией rB(t). Траектория точки B получается переносом траектории точки A в пространстве вдоль вектора AB, который не меняет своей величины и направления во времени (AB = const). Следовательно, траектории всех точек твердого тела одинаковы.Продифференцируем по времени выражение Получаем 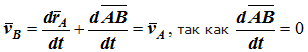 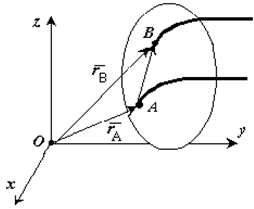 Рис. 1.2 Рис. 1.2Продифференцируем по времени скорость и получим выражение aB = aA. Следовательно, скорости и ускорения всех точек твердого тела одинаковы. Для задания поступательного движения твердого тела достаточно задать движение одной из его точек:  44 Вращательное движение ТВЕРДОГО ТЕЛА угловая скорость угловое ускорения Вращательное движение – это движение твердого тела, имеющего как минимум две неподвижные точки (рисунок 1.3). Прямая, проходящая через эти точки,называется осью вращения. Положение тела определено, если задан угол φ между плоскостями П0 и П , одна из которых неподвижна, а другая жестко связана с телом. φ=φ(t) – уравнение вращательного движения твердого тела.  Рис. 1.3 За положительное направление отсчета принимается вращение против хода часовой стрелки, если смотреть навстречу положительному направлению оси z. Траекториями точек тела при его вращении вокруг неподвижной оси являются окружности, расположенные в плоскостях, перпендикулярных оси вращения.Для характеристики изменения угла поворота с течением времени вводится величина, называемая угловой скоростью ω: Рис. 1.3 За положительное направление отсчета принимается вращение против хода часовой стрелки, если смотреть навстречу положительному направлению оси z. Траекториями точек тела при его вращении вокруг неподвижной оси являются окружности, расположенные в плоскостях, перпендикулярных оси вращения.Для характеристики изменения угла поворота с течением времени вводится величина, называемая угловой скоростью ω:Угловое ускорение – мера изменения угловой скорости:   Рис. 1.4 Рис. 1.4Если ε >0 и ω >0 (рисунок 1.4), то угловая скорость возрастает с течением времени и, следовательно, тело вращается ускоренно в рассматриваемый момент времени в положительную сторону. Направление векторов ω и ε совпадают, оба они направлены в положительную сторону оси вращения Oz.При ε <0 и ω <0 – тело вращается ускоренно в отрицательную сторону. Направление векторов ω и ε совпадают, оба они направлены в отрицательную сторону оси вращения Oz .Если ε <0 и ω >0, то имеем замедленное вращение в положительную сторону. Векторыω и ε направлены в противоположные стороны.Если ε >0 при ω <0, то имеем замедленное вращение в отрицательную сторону. Векторыω и ε направлены в противоположные стороны. Если угловая скорость ω=const, то вращательное движение называется равномерным.Уравнение равномерного вращения φ=φ0+ωt Если угловое ускорение ε=const, то вращательное движение называется равнопеременным. Уравнение равнопеременного вращения  и уравнение, выражающее угловую скорость в любой момент времени и уравнение, выражающее угловую скорость в любой момент времениω=ω0+εt представляют совокупность основных формул вращательного равнопеременного движения тела. 45.Равномерное и равнопеременное вращение.Если угловая скорость тела остается во все время движения постоянной ( =const), то вращение тела называетсяравномерным. Найдем закон равномерного вращения. Из формулы имеем .Отсюда, считая, что в начальный момент времени t=0 угол , и беря интегралы слева от до , а справа от 0 до t, получим окончательно .Из равенства следует, что при равномерном вращении, когда и .В технике скорость равномерного вращения часто определяют числом оборотов в минуту, обозначая эту величину через n об/мин. Найдем зависимость между n об/мин и 1/с. При одном обороте тело повернется на угол , а при n оборотах на ; этот поворот делается за время t = 1 мин = 60 сек. Из равенства следует тогда, что .Если угловое ускорение тела во все время движения остается постоянным , то вращение называется равнопеременным. Найдем закон равнопеременного вращения, считая, что в начальный момент времениt=0 угол , а угловая скорость ( - начальная угловая скорость).Из формулы имеем . Интегрируя левую часть в пределах от до , а правую - в пределах от 0 до t, найдем , или .Вторично интегрируя, найдем отсюда закон равнопеременного вращения .Если величины и имеют одинаковые знаки, то вращение будет равноускоренным, а если разные - равнозамедленным. 46.Скорости и ускорения точек вращающегося тела. 1. Скорости точек тела. Рассмотрим какую-нибудь точку М твердого тела, находящуюся на расстоянииh от оси вращения (см. рис.9). При вращении тела точка М будет описывать окружность радиуса h, плоскость которой перпендикулярна оси вращения, а центр С лежит на самой оси. Если за время dt происходит элементарный поворот тела на угол dφ, то точка М при этом совершает вдоль своей траектории элементарное перемещение ds=hdφ. Тогда числовое значение скорости точки будет равно отношению ds к dt, т.е Скорость в отличие от угловой скорости тела называют иногда еще линейной или окружной скоростью точки М. Таким образом, числовое значение скорости точки вращающегося твердого тела равно произведению угловой скорости тела на расстояние от этой точки до оси вращения. Направлена скорость по касательной к описываемой точкой окружности или перпендикулярно плоскости, проходящей через ось вращения и точку М. Так как для всех точек тела имеет в данный момент времени одно и то же значение, то скорости точек вращающегося тела пропорциональны их расстояниям от оси вращения. Скорость и ускорение точки вращающегося тела Следовательно, линейная скорость любой точки вращающегося тела равна произведению угловой скорости на расстояние от данной точки до оси вращения. Направлена эта скорость всегда по касательной к окружности, которую описывает данная точка при своем движении.  В каждый данный момент времени угловые скорости точек вращающегося тела равны. Поэтому линейные скорости точек тела пропорциональны их расстоянию до оси (рис.3.4), т.е. скорость изменяется полинейному закону. В каждый данный момент времени угловые скорости точек вращающегося тела равны. Поэтому линейные скорости точек тела пропорциональны их расстоянию до оси (рис.3.4), т.е. скорость изменяется полинейному закону.Т  ак как точки тела совершают криволинейное движение (траектории точек - окружности), то полное ускорение слагается из нормального и касательного ускорений , которыеопределяются ак как точки тела совершают криволинейное движение (траектории точек - окружности), то полное ускорение слагается из нормального и касательного ускорений , которыеопределяются (3.14) Таким образом полное ускорение точки будет 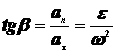 (3.15) Из формул (3.15) следует, что полное ускорение точки вращающегося тела пропорционально ее расстоянию до оси вращения. (3.15) Из формул (3.15) следует, что полное ускорение точки вращающегося тела пропорционально ее расстоянию до оси вращения.При вращательном движении тела вокруг оси нормальное ускорение называют еще центростремительным (вектор направлен по радиусу к центру кривизны), касательное ускорение называют и иначе – вращательным ускорением (вектор ускорения направлен по касательной). 47.Скорость и ускорение точки при векторном способе заданиядвижения С 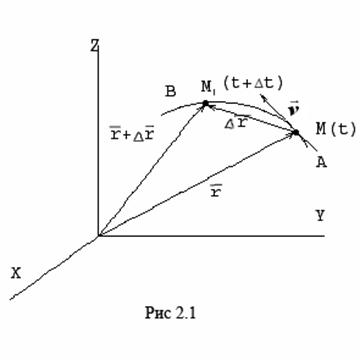 корость точки – это величина, характеризующая как быстро и в каком направлении меняется положение точки в пространстве. Поскольку она определяет направление перемещения точки, скорость является величиной векторной. Пусть за время Δt радиус-вектор точки М изменился на величину Δ. Тогда средней скоростью называется векторная величина корость точки – это величина, характеризующая как быстро и в каком направлении меняется положение точки в пространстве. Поскольку она определяет направление перемещения точки, скорость является величиной векторной. Пусть за время Δt радиус-вектор точки М изменился на величину Δ. Тогда средней скоростью называется векторная величина Этот вектор направлен так же, как и . Предельное значение , при стремящемся к нулю , определит мгновенное значение скорости в данный момент времени При стремлении к нулю хорда ММ1, а значит и вектор поворачивается вокруг точки М, приближаясь к касательной к траектории в точке М и в пределе, совпадая с ней. Поэтому вектор направлен по касательной к траектории точки в сторону движения. В общем случае криволинейного движения вектор скорости изменяется по величине и направлению в функции времени. Следовательно, за время вектор можно представить в виде . Ускорение точки в криволинейном движении характеризует быстроту изменения вектора по величине и направлению. Тогда средняя величина ускорения определится 48.Плоскопараллельное движение твердого тела. Уравнения плоскопараллельного движения. Разложение движения на поступательное и вращательное Плоскопараллельным (или плоским) называется такое движение твердого тела, при, котором все его точки перемещаются параллельно некоторой фиксированной плоскости П (рис. 1). Плоское движение совершают многие части механизмов и машин, например катящееся колесо на прямолинейном участке пути, шатун в кривошипно-ползунном механизме и др. Частным случаем плоскопараллельного движения является вращательное движение твердого тела вокруг неподвижной оси. 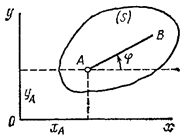 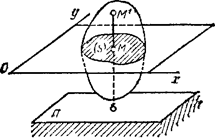 Рис.1 Рис.2 Рассмотрим сечение S тела какой-нибудь плоскости Оxy, параллельной плоскости П (рис.2). При плоскопараллельном движении все точки тела, лежащие на прямой ММ’, перпендикулярной течению S, т. е. плоскости П, движутся тождественно. Отсюда заключаем, что для изучения движения всего тела достаточно изучить, как движется в плоскости Оху сечение S этого тела или некоторая плоская фигураS. Поэтому в дальнейшем вместо плоского движения тела будем рассматривать движение плоской фигуры S в ее плоскости, т.е. в плоскости Оху. Положение фигуры S в плоскости Оху определяется положением какого-нибудь проведенного на этой фигуре отрезка АВ (рис. 28). В свою очередь положение отрезка АВ можно определить, зная координаты xA и yA точки А и угол , который отрезок АВ образует с осью х. Точку А, выбранную для определения положения фигуры S, будем в дальнейшем называть полюсом. При движении фигуры величины xA и yA и будут изменяться. Чтобы знать закон движения, т. е. положение фигуры в плоскости Оху в любой момент времени, надо знать зависимости Уравнения, определяющие закон происходящего движения, называются уравнениями движения плоской фигуры в ее плоскости. Они же являются уравнениями плоскопараллельного движения твердого тела. Первые два из уравнений движения определяют то движение, которое фигура совершала бы при =const; это, очевидно, будет поступательное движение, при котором все точки фигуры движутся так же, как полюс А. Третье уравнение определяет движение, которое фигура совершала бы при Основными кинематическими характеристиками рассматриваемого движения являются скорость и ускорение поступательного движения, равные скорости и ускорению полюса 49 ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА 1. Плоское (плоскопараллельное) движение твердого тела
Плоское (плоскопараллельное) движение твердого тела − это движение, при котором все точки тела движутся в плоскостях, параллельных некоторой неподвижной плоскости (рис. 1). Из определения следует, что перпендикуляр остается параллелен своему начальному положению. По теореме о поступательном движении траектории, скорости и ускорения точек и совпадают. Таким образом, исследование плоского движения твердого тела можно свести к рассмотрению движения плоской фигуры в ее плоскости (рис. 2). Примеры плоского движения скольжение стержня (рис. 3) и качение цилиндра (рис. 4).  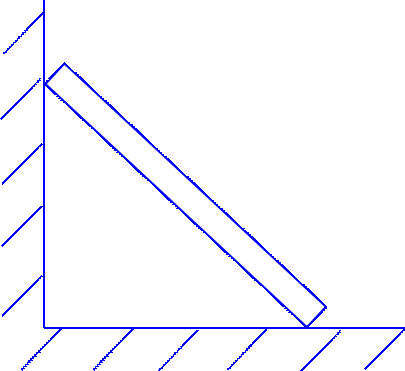
Для задания движения плоской фигуры введем подвижную систему координат (рис. 5), совершающую поступательное движение с точкой . Движение плоской фигуры рассмотрим как сложное, при этом переносное движение − это поступательное движение подвижной системы координат вместе с точкой (полюсом). Относительное движение − это вращение вокруг полюса. Положение плоской фигуры можно задать двумя координатами полюса и одним углом между неподвижной прямой и отрезком, жестко связанным с телом, с указанием положительного направления отсчета: 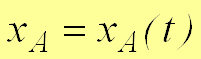 , , 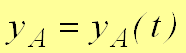 , , При задании плоского движения за полюс может приниматься любая точка тела. Следовательно, вид первых двух уравнений движения зависит от выбора полюса. Закон изменения угла от выбора полюса не зависит. Для характеристики изменения угла поворота плоской фигуры вводится: угловая скорость − 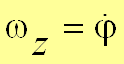 , угловое ускорение , угловое ускорение 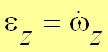 которые не зависят от выбора полюса. |