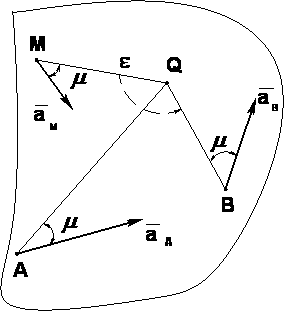
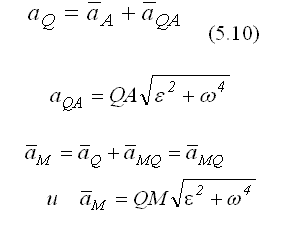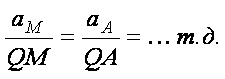Роль механики в подготовке будущего инженерамеханика. Основные этапы развития механики
 Скачать 2.42 Mb.
|
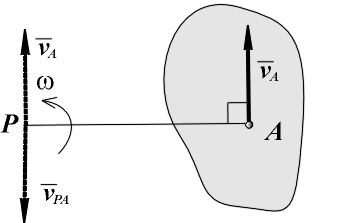
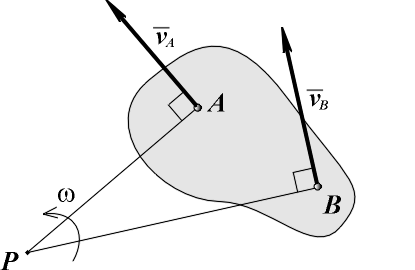
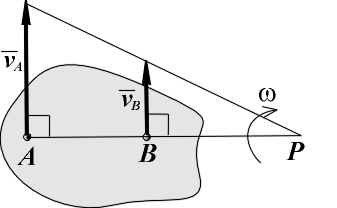
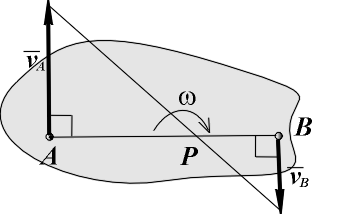
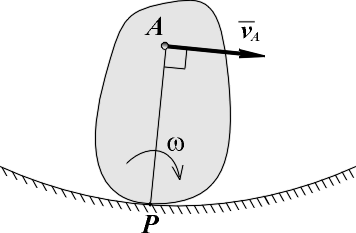
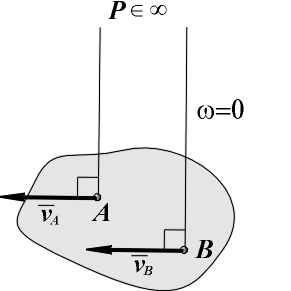
ТЕОРЕМА О ПРОЕКЦИЯХ СКОРОСТЕЙ ДВУХ ТОЧЕК ТЕЛАОпределение скоростей точек плоской фигуры (или тела, движущегося плоскопараллельно) с помощью формулы ( 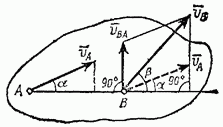 ) связано обычно с довольно сложными расчетами . Однако исходя из этого основного результата, можно получить ряд других, практически более удобных и простых методов определения скоростей точек фигуры (или тела). Рис. 149 Один из таких методов дает теорема: проекции скоростей двух точен твердого тела на ось, проходящую через эти точки, равны друг другу. Рассмотрим какие-нибудь две точки А и В плоской фигуры (или тела). Принимая точку А за полюс (рис. 149), получаем по формуле ( ), что Отсюда, проектируя обе части равенства на ось, направленную по АВ, и учитывая, что вектор перпендикулярен А В, находим и теорема доказана. Заметим, что этот результат ясен и из чисто физических соображений: если равенство ( ) не будет выполняться, то при движении расстояние между точками А и В должно изменяться, что невозможно, так как тело считается абсолютно твердым. Поэтому равенство () выполиася не только при плоскопараллельном, но и при любом движении твердого тела.Доказанная теорема позволяет легко находить скорость данной точки тела, если известны направление скорости этой точки и скорость какой-нибудь другой точки того же тела. 50 Мгновенным центром скоростей называется точка плоскости движения, скорость которой в данное мгновение времени равна нулю. Теорема о существовании мгновенного центра скоростей. Сформулируем теорему, а затем ее докажем. Если тело в плоском движении имеет угловую скорость, то мгновенный центр скоростей существует. На рис. 82 показано тело в плоском движении, причем известны его угловая скорость и скорость одной его точки VA . От точки A отложим отрезок AP = ω / VAперпендикулярно скорости в сторону вращения тела. Выбрав точку A за полюс, определим скорость точки P. Согласно теореме о сложении скоростей VP = VA + VPA . По величине вектор VPA равен VPA = ω AP = VA , но направлен в сторону, противоположную VA (перпендикулярно AP в сторону вращения). Складывая равные по величине, но направленные в разные стороны векторы VA и VPA (рис. 82), получаем VP = 0 , и теорема доказана. Свойства мгновенного центра скоростей. Для доказательства свойств мгновенного центра скоростей определим скорости двух точек тела A и B (рис. 83), выбирая мгновенный центр скоростей P за полюс. По теореме о сложении скоростей VA = VP + VAP; VB = VP + VBP, но VP = 0, и (5) где (6) Анализируя рис. 83 и выражения (5) и (6) можно сформулировать первое свойство мгновенного центра скоростей. Первое свойство. Распределение скоростей точек тела в плоском движении в данное мгновение времени точно такое же, как и при вращении тела вокруг неподвижной оси, которая проходит через мгновенный центр скоростей и перпендикулярна плоскости движения. Заметим, что мгновенный центр скоростей перемещается в плоскости движения (если бы он был неподвижен, было бы вращение вокруг неподвижной оси). Траектория, которую он описывает в неподвижной системе координат, называется неподвижной центроидой, а траектория, которую он описывает в подвижной системе координат, называется подвижной центроидой. Отсюда следует второе свойство мгновенного центра скоростей. Второе свойство. При определении скоростей точек тела плоское движение можно представить как последовательность мгновенных вращений вокруг мгновенного центра скоростей, который сам перемещается в плоскости движения тела. Нахождение мгновенного центра скоростей. Определение положения мгновенного центра в плоскости движения основано на решении системы двух геометрических уравнений из выражений (6): VAAP; VBBP. Мгновенный центр скоростей может быть найден, если известны скорость одной точки тела, например A, и линия действия скорости второй точки тела, например, B (рис. 84). Восстановив перпендикуляры к вектору скорости точки A и к линии действия скорости точки B, находим точку их пересечения P, которая будет единственным решением системы геометрических уравнений и мгновенным центром скоростей. Зная длины отрезков AP и BP и свойства мгновенного центра скоростей, определим направление вращения и величину угловой скорости тела, а затем найдем величину и направление вектора скорости второй точки тела. Вращение тела происходит туда, куда вектор скорости VA первой точки поворачивает тело вокруг мгновенного центра скоростей (в нашем случае на рис. 84 - по часовой стрелке). Вектор скорости VB второй точки тела перпендикулярен своему радиусу вращения (VBBP) и направлен в сторону вращения тела (на рис. 84 - вдоль линии действия вверх). Величины угловой скорости тела и скорости второй точки тела вычисляются по первым двум формулам в выражениях (6): Существуют особые случаи нахождения мгновенного центра скоростей, показанные на рис. 85. На рис. 85, a показан случай, когда перпендикуляры, восстановленные к скорости одной точки тела и к линии действия скорости второй точки тела, параллельны друг другу. Эти перпендикуляры между собой не пересекаются, поэтому AP = и ω = VA / AP = 0. По теореме о сложении скоростей VB = VA + VBA, где VBA = ω·AB. Но ω = 0, и VB = VA. Видим, что тело находится в мгновенно поступательном движении, когда в данное мгновение времени одинаковы только скорости всех точек. Напомним, что при поступательном движении в любой момент времени одинаковы траектории, скорости и ускорения всех точек тела. На рис. 85, b показан случай, когда перпендикуляры, восстановленные к скорости одной точки тела и к линии действия скорости второй точки тела, совпадают друг с другом. Так как перпендикуляры совпали, то система геометрических уравнений имеет бесконечное число решений (у линии, на которой лежат перпендикуляры, существует бесконечное число точек). Для нахождения единственного решения нужно знать вектор скорости второй точки тела, а не только его линию действия. Когда вектор VB известен, мгновенный центр скоростей P находится в точке пересечения перпендикуляров с линией, соединяющей концы векторов скоростей VA и VB. Остается определить направление вращения тела и величину угловой скорости, равную ω = VA / AP = VB / BP. На рис. 85, c показано качение колеса без скольжения по неподвижной поверхности. В этом случае положение мгновенного центра можно найти из физических соображений, используя результаты примера 2 предыдущего раздела. Так как скорости всех точек неподвижной поверхности равны нулю, а при качении без скольжения скорости точек касания тел одинаковы, то в точке касания колеса с неподвижной поверхностью будет находиться мгновенный центр скоростей P колеса. На том же рисунке жирными точками отмечены последовательные положения мгновенного центра скоростей на колесе и на неподвижной поверхности при качении колеса. Мы видим, что мгновенный центр скоростей перемещается в плоскости движения; неподвижной центроидой является прямая линия; подвижной центроидой является окружность, радиус которой равен радиусу колеса. Если рассматривать оба шасси При повороте задних колес в ту же сторону, что и передние, мгновенный центр поворота (МЦП) отдаляется, траектория спрямляется, а поперечные силы ослабевают, а нагрузка на резину снижается На низких скоростях МЦП приближаются к авто, что повышает верткость на парковке Если рассматривать систему одного шасси и два повернутых колеса, то рисунок будет выглядеть примерно так: Если скорости точек А и В (рис) взаимно параллельны, а точки лежат на общем перпендикуляре к скоростям, то МЦС (точка Р) находится на пересечении указанного общего перпендикуляра АВ и прямой 1–1, проведенной через концы векторов скоростей этих точек. Где Va - скорость правого колеса
плоской фигуры с использованием мгновенного центра скоростей  Мгновенным центром скоростей (МЦС) плоской фигуры называется точка P, скорость которой в данный моментвремени равна нулю: vP 0 . МЦС может быть конкретной точкой плоской фигуры или может располагаться вне плоской фигуры. В последнем случае его следует понимать как точку подвижной плоскости, жестко скрепленной с плоской фигурой. При движении плоской фигуры положение МЦС может изменяться как относительно самой фигуры, так и относительно неподвижной системы отсчета. Использование МЦС упрощает процедуру определения скоростей точек плоской фигуры. Пусть в данный момент времени известно положение МЦС (точка P) и известна угловая скорость плоской фигуры (рис. 11). 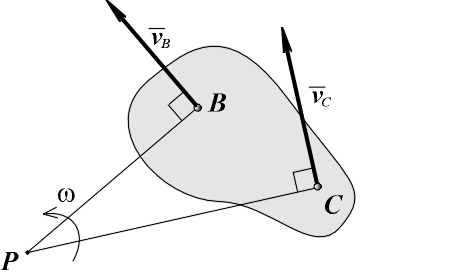 Рис 11. Определение скоростей точек B и C с использованием мгновенного центра скоростей P. Возьмем точку P для этого момента времени в качестве полюса, скорость которогоvP 0 . Тогда согласно формуле (2.15) скорость какой-либо точки B vB vP
Направление скорости v Bперпендикулярно отрезку PB и ее модуль vB vBA PB . Аналогичный результат получается для другой точки C:vC vCP ;vC vCA PC ; (vC PC ). Таким образом, скорости точек плоской фигуры пропорциональны их расстояниям до МЦС и определяются в данный момент времени так, как если бы движение фигуры было вращением вокруг МЦС. 
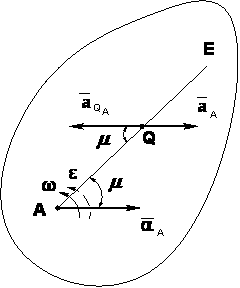
52,53,54. 52. Определение скоростей и ускорений точек при плоском движении На рисунке изображен плоский кривошипно-ползунный механизм. Звено ОА вращается вокруг точки О по закону ϕ(t)=π/3t2 радиан. Известны длины звеньев OA и AB. Найти скорость и ускорение точки B, а также угловую скорость и угловое ускорение звена AB в момент времени t=1c. На рисунке изображен механизм в положении, соответствующем моменту времени t=1c. В этот момент времени между звеньями OA и AB прямой угол. 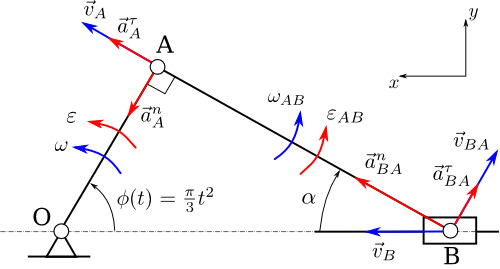 Для определения скорости точки B запишем теорему о скоростях плоской фигуры AB, выбрав за полюс точку А: v⃗ B=v⃗ A+v⃗ BA. (1) Скорость точки А определим, зная что эта точка вращается вместе со звеном ОА вокруг точки А: vA=ωOA=ϕ˙(t)OA Скорость точки А будет направлена перпендикулярно звену ОА. В уравнении (1) известно направление скорости точки B: скорость точки B направлена по горизантали. Пусть v⃗ B направлена справа налево, в результате дальнейших вычислений знак в выражении для vB покажет истинное направление скорости v⃗ B. Известно также направление скорости точки B при её движении вокруг полюса А: v⃗ BA⊥AB. Величина этой скорости определяется следующим образом: vBA=ωABAB, где ωAB - угловая скорость звена AB. Для определения неизвестных, входящих в векторное уравнение (1) (скорость точки B и угловая скорость ωAB), спроецируем это векторное уравнение на вертикальную и горизонтальную оси. Проекция векторов уравнения на ось x: vB=vAsinϕ+vBAcosα. Проекция векторов уравнения на ось x: 0=vAcosϕ+vBAsinα. Из последнего уравнения определяем vBA и угловую скорость звена AB: vBA=−vAcosϕsinα, ωAB=−vAcosϕABsinα. Знак минус перед выражением для vBA и ωAB говорит о том, что действительное направление угловой скорости звена AB отличается от того что показано на рисунке. Подставляя vBA в первое уравнение, найдем скорость точки B: vB=vAsinϕ−vAcosϕtanα. Ускорение точки B определим, используя теорему об ускорениях: a⃗ B=a⃗ A+a⃗ nBA+a⃗ τBA. Точка A вращается вместе с телом OA с известным угловым ускорением и угловой скоростью. Ускорение точки А будет складываться из вращательного и осестремительного ускорений: a⃗ A=a⃗ τA+a⃗ nA. Осестремительное ускорение, направленное к оси вращения, определится следующим образом: anA=ω2OA=ϕ˙(t)OA Вращательное ускорение точки А, перпендикулярно ОА и равно: aτA=εOA=ω˙OA=ϕ¨(t)OA Ускорение точки В, входящее в уравнение (1) направено вдоль оси x. Предположим, что ускорение a⃗ B направлено справа налево. Направления компонент полного ускорение точки B при ее движении вокруг точки А: a⃗ nBA и a⃗ τBA, показаны на рисунке. Зная угловую скорость вращения звена АВ, определим осестремительное ускорение точки В при её движении вокруг полюса (точка А): anBA=ω2ABAB. Вращательное ускорение точки В вокруг полюса выражается следующим образом: aτBA=εABAB. Спроецируем векторное уравнение на оси x и y. Проекция на ось x: aB=anAcosϕ+aτAsinϕ+anBAcosα−aτBAsinα. Проекция на ось y: 0=−anAsinϕ+aτAcosϕ+anBAsinα+aτBAcosα. Из последнего уравнения определяем вращательное ускорение точки В вокруг полюса и угловое ускорение звена АВ: aτBA=anAsinϕ−aτAcosϕ−anBAsinαcosα, εAB=aτBAAB. Подставив aτBA, найдем ускорение точки B: aB=anAcosϕ+aτAsinϕ+anBAcosα−(anAsinϕ−aτAcosϕ−anBAsinα)tanα. 53. Мгновенный центр ускорений – точка (Q) плоской фигуры, ускорение которой в данный момент времени равно нулю. Для его построения из точки А откладываем под углом  к ускорению аА отрезок  , при этом угол откладывается от ускорения в сторону, направления углового ускорения e. Модули ускорений точек плоской фигуры пропорциональны расстояниям от этих точек до мгн.ц. ускорений, а векторы ускорений составляют с отрезками, соединяющими эти точки и м.ц.у. один и тот же угол  :  . Мгновенный центр скоростей Р и мгновенный центр ускорений Q являются различными точками плоской фигуры.Определение ускорений точек тела с помощью М.Ц.У.
Следовательно, ускорение любой точки тела равно ее ускорению во вращательном движении вокруг мгновенного центра ускоренийQ.
То есть ускорения точек тела пропорционально их расстояниям от мгновенного центра ускорений. Положение мгновенного центра ускорений и мгновенного центра скоростей в общем случае в любой данный момент времени не совпадают. 54 Сферическое движение твердого тела. Эйлеровы углы. Уравнения сферического движения. Сферическим движением (движением тела с одной закрепленной точкой) называется такое движение тела, при котором одна его точка О остается неподвижной во все время движения. Все остальные точки тела движутся при этом по траекториям, расположенным на поверхности сфер с центром в неподвижной точке О. Положение тела определяется углами Эйлера (рис. 1): углом прецессии φ, углом нутации θ и углом собственного вращения φ. Эти углы характеризуют положение координатного трехгранника осей Oξηζ, связанного с телом, по отношению к неподвижному трехграннику Oxyz. Линия ON пересечения координатных плоскостей Оху и Oξη называется линией узлов.  | ||||||||||||||||||||||||||||||||||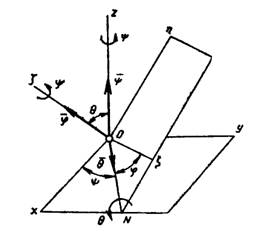
