Роль механики в подготовке будущего инженерамеханика. Основные этапы развития механики

• Название: Роль механики в подготовке будущего инженерамеханика. Основные этапы развития механики
• Анкор: Shpory_po_teor meh.doc
• Дата: 07.04.2017
• Размер: 2.42 Mb.
• Имя файла: Shpory_po_teor meh.doc
• Тип: Документы; #4582
• страница: 3 из 8

Метод вырезания узлов.

Этим методом удобно пользоваться, когда надо найти усилия во всех стержнях фермы. Он сводится к последовательному рассмотрению условий равновесия сил, сходящихся в каждом из узлов, определению усилий в стержнях фермы.

Активные силы и реакции опор являются внешними силами для всей фермы, рассматриваемой как твердое тело; усилия в стержнях в этом случае - внутренние силы. Поэтому для определения усилий необходимо рассмотреть равновесие части фермы, для которой искомые усилия являются внешними силами.

При решении задач на расчете ферм способом вырезания узлов необходимо придерживаться следующего плана действий:

1. Выбор тела (или т ел),равновесие которого должно быть рассмотрено.

2. Когда заданные силы действуют на одно тело, а искомые на другое или когда те и другие силы действуют одновременно на несколько тел, может оказаться необходимым рассмотреть равновесие системы этих тел или последовательно равновесие каждого тела в отдельности.

3. Изображение действующих (активных) сил. Установив равновесие какого тела или тел рассматривается (и только после этого), следует на чертеже изобразить все действующие на это тело, (или тела) внешние силы, включая как заданные, таи и искомые сковы, в том числе реакции всех связей.

4. Составление условий равновесия. Условия равновесия составляют для сил, действующих на тело (или тела), равновесие которых рассматривается.

5. Определение ,реакции опор, пользуясь уравнениями равновесия для всей фермы, рассматриваемой как твердое тело, проверка правильности решения и исследование полученных результатов.

6. Вырезать узел, в котором сходятся два стержня, и рассмотреть его равновесие под действием активных сил и реакций разрезанных стержней; определить эти реакции

7. Переходя от узла к узлу, рассматривать аналогично равновесие каждого узла.

методом Риттера

Этим методом удобно пользоваться для определения усилий в отдельных стержнях фермы, например, для проверочных расчетов (рис. 4)

При расчете методом сечении рекомендуется такая последовательность действии:

1. Определить реакции опор, пользуясь уравнениями равновесия для всей фермы, рассматриваемой как твердое тело, находящееся под действием плоской системы сил.

2. Ферму разделяют на две части сечением, проходящим через три стержня, в которых (или в одном из которых) требуется определить усилия, и рассматривают равновесие одной из этих частей. Действие отброшенной части заменяют соответствующими силами, направляя их вдоль разрезанных стержней от узлов, т. е., считая их растянутыми.

3. Затем составляются уравнения равновесия так, чтобы в каждое уравнение входило одно неизвестное усилие.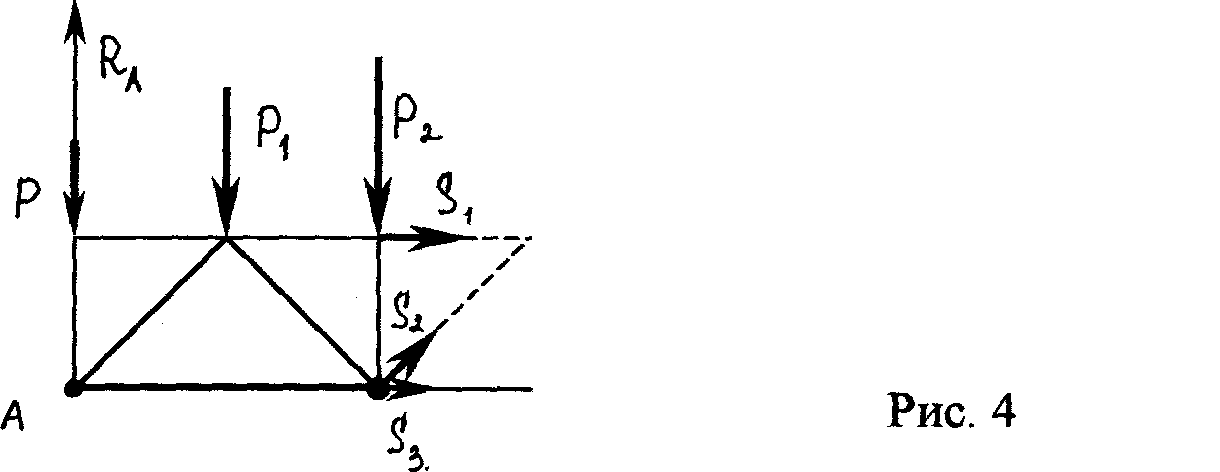



4. Из полученных уравнений находятся неизвестные усилия в стержнях; если в ответе получается знак «-», то это означает, что стержень сжат, а не растянут.

25.Векторный момент силы относительно центра. Выражение векторного момента силы в виде векторного произведения.

Векторный момент силы относительно центра – векторное произведение радиус-вектора точи приложения силы относительно центра на вектор силы.

Теорема Вариньона: Если система сил, приложенных к абсолютно твердому телу имеет равнодействующую, то момент равнодействующей относительно произвольного центра (оси) равен сумме моментов всех сил системы относительно того же центра (оси).

Алгебраическим моментом силы F относительно некоторого центра называется взятое со знаком + или - произведение модуля силы F на плечо (кротчайшее расстояние от точки до линии действия силы). Момент положителен, если сила стремиться вращать плоскость действия против часовой стрелки и наоборот. (M=F*h) Но при этом h можно выразить через радиус-вектор r (h=r*sin α), тогда M = F*r*sin α = (F x r). Получаем, что векторный момент силы относительно точки – векторная величина.
26. Момент силы относительно оси. Аналитическое выражение момента силы относительно оси.

Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью


Момент относительно оси положителен, если сила стремится вращать плоскость перпендикулярную оси против часовой стрелки, если смотреть навстречу оси.

Момент силы относительно оси равен 0 в двух случаях:

• 
  Если сила параллельна оси
  
• 
  Если сила пересекает ось
  

Если линия действия и ось лежат в одной плоскости, то момент силы относительно оси равен 0.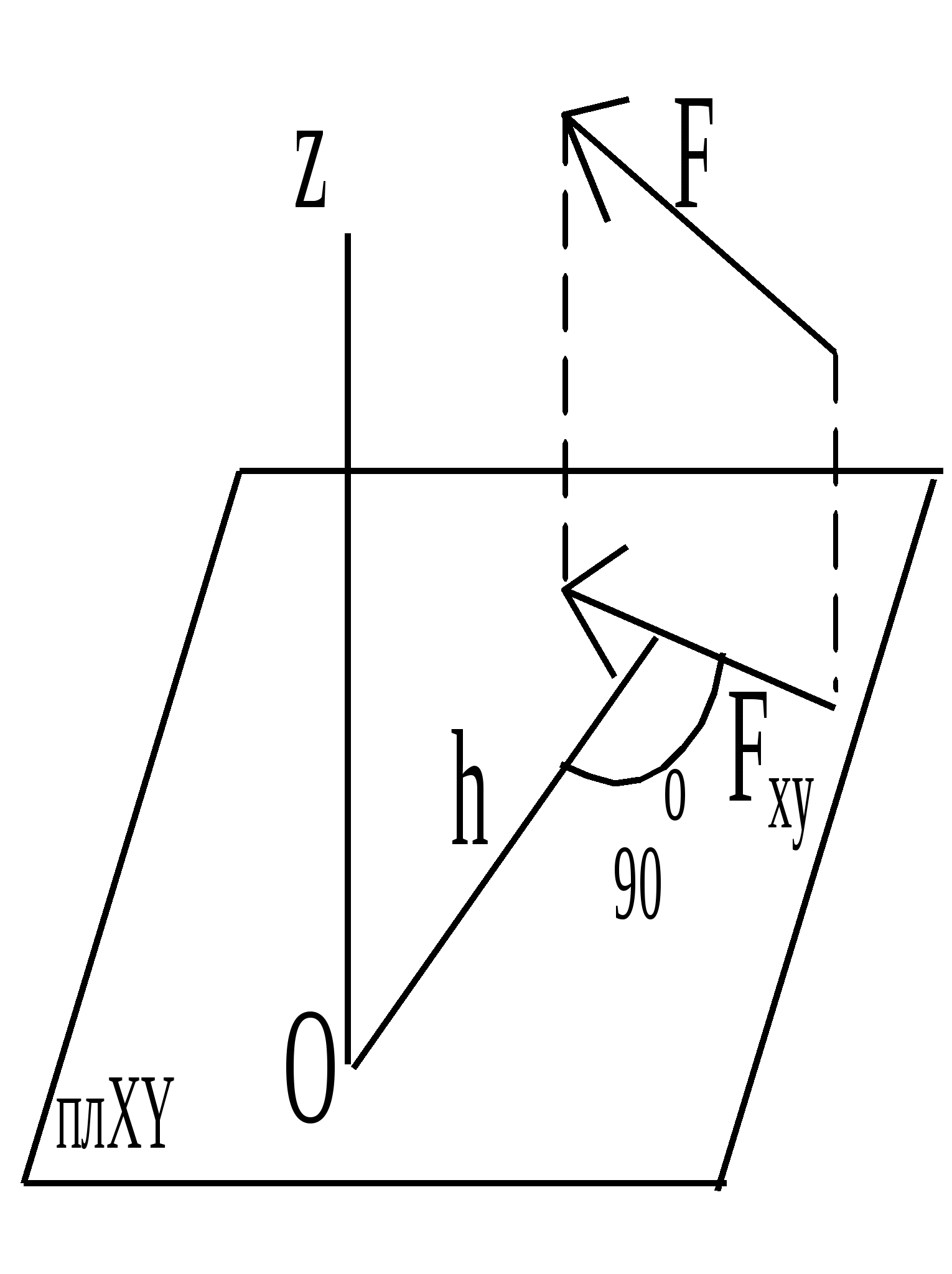




27. Связь между моментом силы относительно оси и векторным моментом силы относительно точки.

Mz(F)=Mo(F)*cosα Момент силы, относительно оси равен прекции вектора момента сил, относительно точки оси на эту ось.
28. Основная теорема статики о приведении системы сил к заданному центру (теорема Пуансо). Главный вектор и главный момент системы сил.

Всякую пространственную систему сил в общем случае можно заменить эквивалентной системой, состоящей из одной силы, прило­женной в какой-либо точке тела (центре приведения) и равной глав­ному вектору данной системы сил, и одной пары сил, момент которой равен главному моменту всех сил относительно выбранного центра приведения. 



Главным вектором системы сил называется вектор R, равный векторной сумме этих сил:

R = F₁ + F₂ + ... + F_n =  F_i.

Для плоской системы сил ее главный вектор лежит в плоскости действия этих сил.

Главным моментом системы сил относительно центра O называется вектор L_O, равный сумме векторных моментов этих сил относительно точки О:

L_O = M_O(F₁) + M_O(F₂) + ... + M_O(F_n) =  M_O(F_i).

Вектор R не зависит от выбора центра О, а вектор L_O при изменении положения центра О может в общем случае изменяться.

Теорема Пуансо: Произвольную пространственную систему сил можно заменить одной силой главным вектором системы сил и парой сил с главным моментом не нарушая состояния твердого тела. Главный вектор представляет собой геометрическую сумму всех сил действующих на твердое тело и расположен в плоскости действия сил. Главный вектор рассматривается через его проекции на оси координат.

Чтобы привести силы к заданному центру приложенному в некоторой точке твердого тела необходимо: 1) перенести параллельно силу самой себе к заданному центру не изменяя модуля силы; 2) в заданном центре приложить пару сил, векторный момент которой равен векторному моменту перенесенной силы относительного нового центра, эту пару называют присоединенной парой.

Зависимость главного момента от выбора центра приведения. Главный момент относительно нового центра приведения равен геометрической сумме главного момента относительно старого центра приведения и векторного произведения радиуса-вектора, соединяющего новый центр приведения со старым, на главный вектор.


29 Частные случаи приведения пространственной системы сил

№	Значения главного вектора и главного момента	Результат приведения
1		Система сил приводится к паре сил, момент которой равен главному моменту  (главный момент системы сил не зависит от выбора центра приведения О).
2		Система сил приводится к равнодействующей, равной , проходящей через центр О.
3		Система сил приводится к равнодействующей , равной главному вектору  и параллельной ему и отстоит от него на расстоянии . Положение линии действия равнодействующей должно быть таким, чтобы направление ее момента относительно центра приведения О совпадало с направлением  относительно центра О.
4	, причем векторы  и  не перпендикулярны	Система сил приводится к динаме (силовому винту) – совокупности силы  и  пары сил, лежащей в плоскости, перпендикулярной к этой силе.
5		Система сил, приложенных к твердому телу, является уравновешивающейся.

30. Приведение к динаме. Динамой в механике называют такую совокупность силы и пары сил () действующих на твердое тело, у которой сила перпендикулярна плоскости действия пары сил. Используя векторный момент пары сил , можно также определить динаму как совокупность силы и пары, у которы сила параллельна векторному моменту пары сил.

Уравнение центральной винтовой осиПредположим, что в центре приведения, принятом за начало координат, получены главный вектор с проекциями на оси координат и главный момент с проекциями При приведении системы сил к центру приведения О₁ (рис. 30) получается динама с главным вектором и главным моментом , Векторы и как образующие линаму. параллельны и поэтому могут отличаться только скалярным множителем k_0. Имеем,, так как .Главные моменты и , удовлетворяют соотношению



Подставляя , получим



 Координаты точки О₁ в которой получена динама, обозначим х, у, z. Тогда проекции вектора на оси координат равны координатам х, у, z. Учитывая это, (*) можно выразить в форме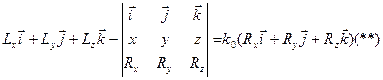



где i. j ,k - единичные векторы осей координат, а векторное произведение *представлено определителем. Векторное уравнение (**) эквивалентно трем скалярным, которые после отбрасывания можно представить в виде



Полученные линейные уравнения для координат х, у, z являются уравнениями прямой линии - центральной винтовой оси. Следовательно, существует прямая, в точках которой система сил приводится к динаме.

31 Условия и уровнения пространственной системы сил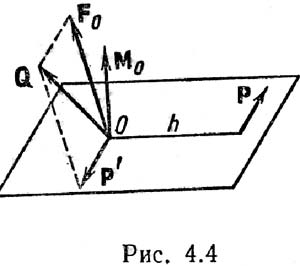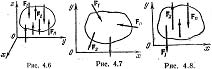





Для равновесия пространственной системы сил необходимо и достаточно, чтобы главный вектор и главный момент этой системы равнялись нулю. Достаточность: при F_o=0 система сходящихся сил, приложенных в центре при­ведения О, эквивалентна нулю, а при М_о=0 система пар сил эквивалентна нулю. Следовательно, исходная система сил эквива­лентна нулю. Необходимость: Пусть данная система сил эквивалентна нулю. Приведя систему к двум силам, заметим, что система сил Q и Р (рис. 4.4) должна быть эк­вивалентна нулю, следовательно, эти две силы должны иметь общую линию действия и должно выполняться рав-во Q=–Р. Но это может быть, если линия действия силы Р проходит через точку О, т. е. если h=0. А это значит, что главный момент равен нулю (М_о=0). Т.к. Q+Р=0, a Q=F_o+P', то F_o+P'+P=0, и, следовательно, F_o = 0. Необх и достуслравновпро­странственнойсист сил им вид: F_o=0, M_o=0 (4.15),

или,  в проекциях на  координатные оси, Fox=åF_kx=F_1x+F_2x+…+F_nx=0; F_Oy=åF_ky=F_1y+F_2y+...+F_ny=0; F_oz=åF_kz=F_1z+F_2z+…+F_nz=0 (4.16).   M_Ox=åM_Ox(F_k)=M_Ox(F₁)+М_ox(F₂)+...+M_Ox(F_n)=0, M_Oy=åM_Oy(F_k)=M_oy(F₁)+M_oy(F₂)+…+M_oy(F_n)=0, М_oz=åМ_Оz(F_k)=М_Оz(F₁)+M_oz (F₂)+...+М_oz(F_n)=0. (4.17)

Т.о. при решении задач имея 6 ур-ий можно найти 6 неизвестных. Замечание: пару сил нельзя привести к равнодействующей. Частные случаи: 1) Равновесие пространственной системы параллельных сил. Пусть ось Z параллельна линиям действ силы (рис 4.6), тогда проекции сил на x и y равны 0 (F_kx=0 и F_ky=0), а остаётся только F_oz. А что касается моментов, то остаются только M_ox и M_oy, а M_ozотсутствует. 2) Равновесие плоской системы сил. Остаются ур-я F_ox, F_oy и момент M_oz (рис 4.7). 3) Равновесие плоской системы параллельных сил. (рис. 4.8). Остаются только 2 ур-я: F_oy и M_oz.При составлении ур-ий равновесия за центр привидения может быть выбрана любая точка.

Если система сил находится в равновесии, то ее главный вектор и главный момент равны нулю:



Эти векторные равенства приводят к следующим шести скалярным равенствам: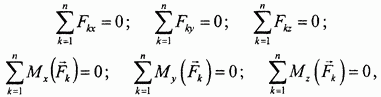



которые называются условиями равновесия пространственной произвольной системы сил.

32 теорема Вариньона, согласно которой моментравнодействующей системы сил относительно какого-либо центра равен геометрической сумме моментов составляющих систему сил относительно того же центра.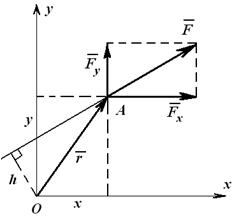


Рисунок 1.17

    Например, момент силы F  относительно точки  O можно определить как алгебраическую сумму моментов сил F_x  и  F_y (на которые можно разложить силу F ) относительно той же точки O  (рисунок 1.17). То есть
 M_o(F)= -Fh = -F_x y+ F_y x,  (1.8)
где  F_x , F_y ,  x и y  – проекции на оси координат силы F и радиуса-вектора r .
33Центр параллельных сил

Рассмотрим систему параллельных сил  {F1, F2, ..., Fn}. При повороте всех сил системы на один и тот же угол линия действия равнодействующей системы параллельных сил повернется в ту же сторону на тот же угол вокруг некоторой точки (рисунок 1.5, а). Эта точка называется центром параллельных сил.  Согласно теореме Вариньона, если система сил имеет равнодействующую, то ее момент относительно любого центра (оси) равен сумме моментов всех сил системы относительно того же центра (оси). Рисунок 1.5 Для определения координат центра параллельных сил воспользуемся этой теоремой. Относительно оси x  Mx(R) = ΣMx(Fk),   - yCR= ΣykFk        и        yC = ΣykFk /ΣFk. Относительно оси y   My(R) = ΣMy(Fk),       - xCR = ΣxkFk        и       xC = ΣxkFk /ΣFk. Чтобы определить координату  zC, повернем все силы на 90° так, чтобы они стали параллельны оси  y (рисунок 1.5, б). Тогда  Mz(R) = ΣMz(Fk),        - zCR = ΣzkFk        и       zC = ΣzkFk /ΣFk. Следовательно, формула для определения радиус-вектора центра параллельных сил принимает вид  rC = ΣrkFk /ΣFk. Свойства центра параллельных сил: 1 Сумма моментов всех сил  Fk  относительно точки  C  равна нулю   ΣMC(Fk) = 0. 2 Если все силы повернуть на некоторый угол  α, не меняя точек приложения сил, то центр новой системы параллельных сил будет той же точкой  C.