Определение реакций опор для балочных систем
 Скачать 2.27 Mb. Скачать 2.27 Mb.
|
Практическая работа 1 Тема: Определение реакций опор для балочных систем Цель работы: Закрепить теоретические знания и умения определять реакции в опорах балочных систем Студент должен знать основные понятия и законы механики твердого тела. Форма работы - индивидуальная. Краткие теоретические и справочно-информационные материалы по теме: Очень часто в машинах и конструкциях встречаются тела удлиненной формы, называемые балками (или балочными системами). Балки в основном предназначены для восприятия поперечных нагрузок. Балки имеют специальные опорные устройства для сопряжения их с другими элементами и передачи на них усилий. Неизвестные числовые значения реакций опорных устройств балки определяются через систему уравнений равновесия. Уравнения равновесия произвольной плоской системы сил могут быть представлены в трех формах. Первая (основная форма этих уравнений): При решении многих задач рациональнее пользоваться другими формами уравнений равновесия. Так как при равновесии твердого тела сумма моментов всех приложенных к нему сил относительно любой точки равна нулю, то можно, выбрав три произвольные точки А, В, С и приравняв нулю сумму моментов относительно каждой из них, получить три следующих уравнения равновесия: Это вторая форма уравнений равновесия. Третья форма уравнений равновесия представляет собой равенство нулю сумм моментов относительно двух произвольных точек А и В и равенство нулю суммы проекций на некоторую ось х: Первая форма уравнений равновесия для плоской системы параллельных сил примет вид: Вторая и третья формы уравнений равновесия для плоской системы параллельных сил примут одинаковый вид: Итак, для произвольной плоской системы сил имеем три уравнения равновесия, а для плоской системы параллельных сил — только два. Соответственно при решении задач на равновесие произвольной плоской системы сил можно найти три неизвестных, а при рассмотрении равновесия плоской системы параллельных сил — не более двух. Для контроля правильности решения используют дополнительное уравнение/ Задание 1. Определить величины реакций в заделке. Провести проверку правильности решения. Задание 2. Определить величины реакций в шарнирных опорах балки. Провести проверку правильности решения. Порядок выполнения работы: 1. Заменить распределенную нагрузку ее равнодействующей и указать точку ее приложения. 2. Освободить балку от связей, заменив их реакциями. 3. Выбрать систему уравнений равновесия. 4. Решить уравнения равновесия. 5. Выполнить проверку решения. Примеры расчета: Задание 1. Определить величины реакций в заделке. Провести проверку правильности решения. 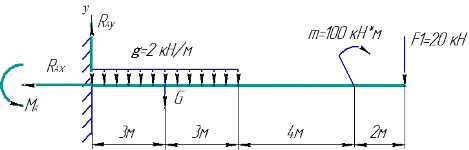 Решение: 1. Заменяем распределенную нагрузку сосредоточенной G = q × l ; G = 2 × 6 = 12 кН 2. Освобождаем балку АВ от связей, отбрасываем заделку в точке А и заменяем действие заделки возможными реакциями, возникающими в опоре – реактивным моментом МА и составляющими реакциями RAx и RAy. Получили плоскую систему параллельно расположенных сил, значит RAx = 0. 3. Выбираем систему уравнений равновесия: 4. Решение начинаем с крайней левой точки.  В уравнении учитываем все моменты, которые создаются действующими силами находящимися на расстоянии относительно точки А. (Реакции, находящиеся в точке А, в уравнении не учитываются, так как они не создают плеча с точкой).  Знаки полученных реакций (+), следовательно, направления реакций выбраны, верно. 5. Для проверки правильности решения составляем уравнение моментов относительно точки В. В уравнении учитываем все моменты, которые создаются действующими силами, находящимися на определенном расстоянии от точки В. Решение выполнено, верно. Задание 2. Определить величины реакций в шарнирных опорах балки. Провести проверку правильности решения 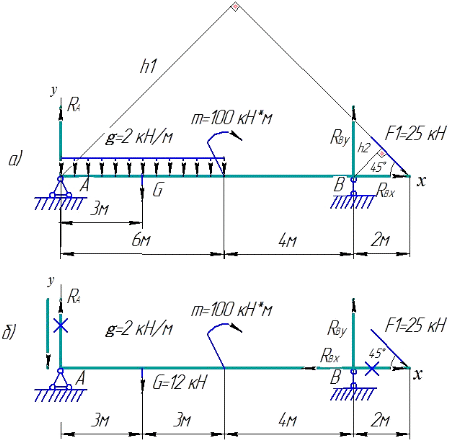 Решение: Обозначаем опоры точками. Левая опора (точка А) – подвижный шарнир, правая опора (точка Б) – неподвижный шарнир. 2. Заменяем распределенную нагрузку сосредоточенной G = q × l ; G = 2 × 6 = 12 кН 3. Освобождаем балку от связей в точках А и В и заменяем их возможными реакциями, возникающими в опорах. В шарнирно-подвижной опоре А может возникнуть реакция RAy, перпендикулярная к опорной поверхности, в шарнирно-неподвижной опоре В – две составляющие реакции: вертикальная RBy и горизонтальная RBx. Получили плоскую систему произвольно расположенных сил. 4. Для решения выбираем уравнение равновесия в виде  5. Решение начинаем с крайней левой точки. В уравнении учитываем все моменты, которые создаются действующими силами. находящимися на расстоянии относительно точки А.(Реакции находящиеся в точке А, в уравнении не учитываются, так как они не создают плеча с точкой).  Реакция направлена правильно. В уравнении учитываем все моменты, которые создаются действующими силами, находящимися на расстоянии относительно точки В.(Реакции, находящиеся в точке В, в уравнении не учитываются, так как они не создают плеча с точкой).  Реакция отрицательная, следовательно, нужно направить в противоположную сторону. Начиная решение с крайней левой точки, в уравнении учитываем все вектора сил, которые проецируются на ось х. 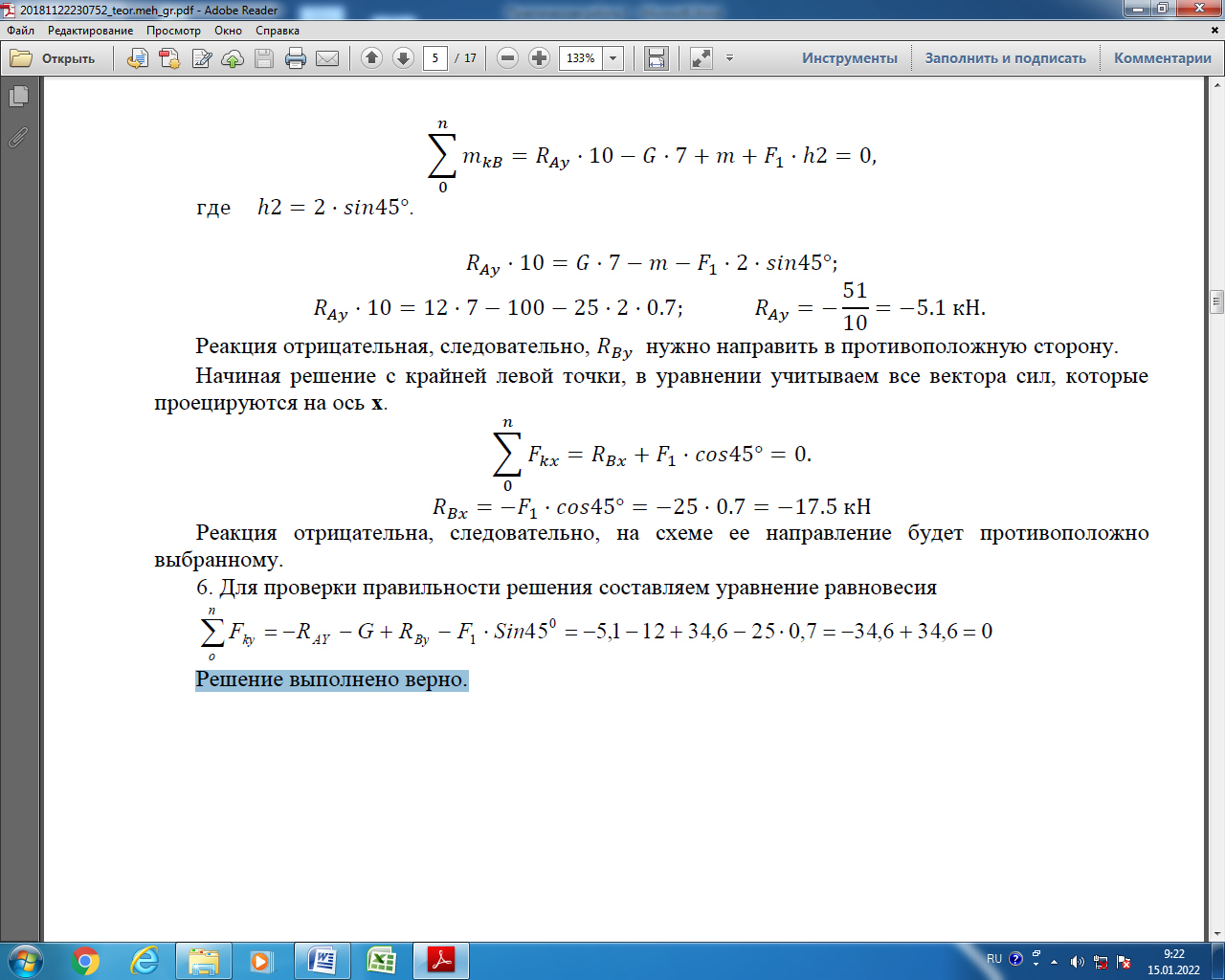 Реакция отрицательна, следовательно, на схеме ее направление будет противоположно выбранному. 6. Для проверки правильности решения составляем уравнение равновесия Решение выполнено верно. 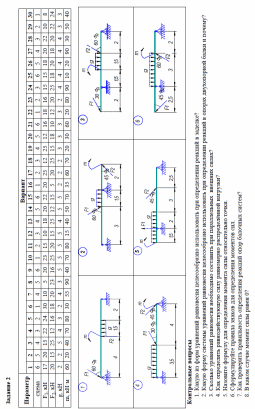 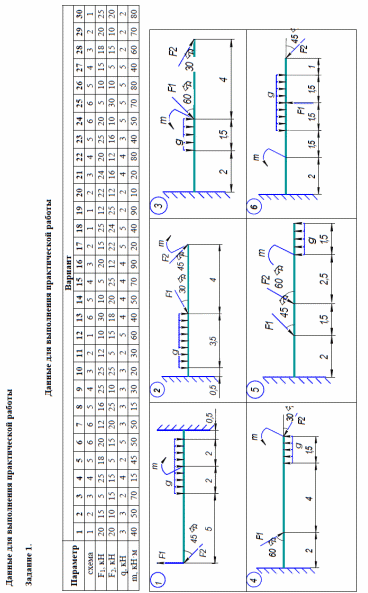 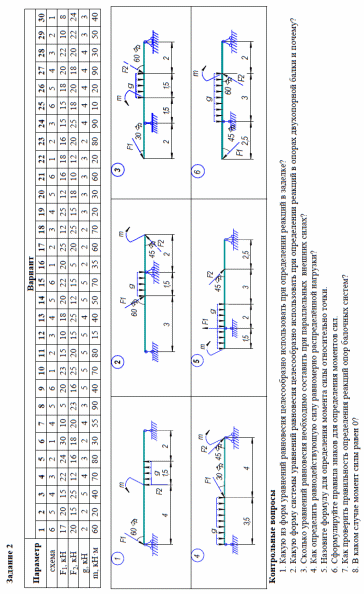 |
