солянка матеша. солянка из матеши. Определенный интеграл от функции по отрезку это предел интегральных сумм при. Геометрический смысл определенного интеграла заключается в том, что его значением является площадь криволинейной трапеции для непрерывной и неотрицательной функции вида расположенной на интервале.
 Скачать 6.87 Mb. Скачать 6.87 Mb.
|
Вычисление криволинейного интеграла I родаВычисление криволинейного интеграла I рода может быть сведено к вычислению определенного интеграла. Некоторые приложения криволинейного интеграла I родаКриволинейный интеграл I рода имеет разнообразные приложения в математике и механике. Длина кривойДлина I кривой АВ плоской или пространственной линии вычисляется по формуле 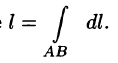 Плоиодь цилиндрической поверхностиЕсли направляющей цилиндрической поверхности служит кривая АВ, лежащая в плоскости Оху, а образующая параллельна оси Oz (см. рис. 235), то площадь поверхности, задаваемой функцией z = f(x; у), находится по формуле 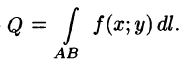 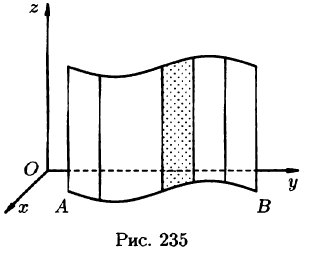 Масса кривойМасса материальной кривой АВ определяется формулой 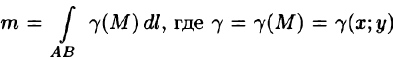 — плотность кривой в точке М. — плотность кривой в точке М.Разобьем кривую АВ на п элементарных дуг Пусть Суммируя, находим приближенное значение массы m: 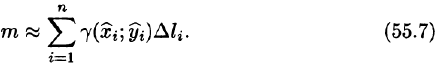 За массу кривой АВ примем предел суммы (55.7) при условии, что 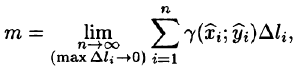 или, согласно формуле (55.2), 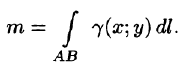 (Заметим, что предел существует, если кривая АВ гладкая, а плотность задана непрерывной в каждой точке АВ функцией.) Статические моменты, центр тяжестиСтатические моменты относительно осей Ох и Оу и координаты центра тяжести материальной кривой АВ определяются по формулам 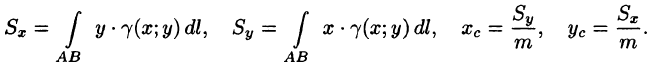 Моменты инерцииДля материальной кривой АВ моменты 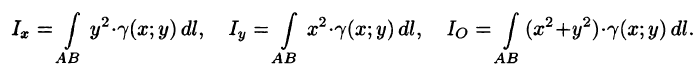 17. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ 2-ГО РОДА      18. Циркуляция. Условие независимости криволинейного интеграла от формы пути интегрирования. Теорема  Циркуляция векторного поля по замкнутому контуру равна потоку его ротора через поверхность, натянутую на данный контур в направлении, которое соответствует направлению обхода контура: а именно, если смотреть на поверхность из острия её нормальных векторов (вектора), то путь по контуру должен быть виден нам, как осуществляемый ПРОТИВ часовой стрелки. Циркуляция (Ц) векторного поля по контуру – это скалярная величина, численно равная криволинейному интегралу 2-го рода по этому контуру: 19. Формула Стокса. Ротор векторного поля, его физический смысл свойства. Формула Стокса. Циркуляция векторного поля по замкнутому контуру равна потоку его ротора через поверхность , натянутую на данный контур в направлении, которое соответствует направлению обхода контура: В качестве еще одной важной меры направленности физического поля выступает характеристика, получившая название ротор или вихрь. Ротор {вихрь) - это векторный дифференциальный оператор над векторным полем. Ротор поля F обозначается символом rot F, он определяется векторным произведением где V - векторный дифференциальный оператор набла. Результат действия этого оператора на конкретное векторное поле F представляет собой новое векторное поле. Физически поле ротора F, т.е. длина и направление вектора rot F в каждой точке пространства, характеризует в некотором смысле вращательную составляющую поля F соответственно в каждой точке. Или по-другому показывает, насколько и в каком направлении закручено поле в каждой точке. Математически ротор векторного поля F - есть вектор, проекция которого rotnF на каждое направление п равна пределу отношения циркуляции векторного поля по замкнутому контуру L, являющемуся краем плоской площадки AS, перпендикулярной к этому направлению, к величине этой площадки, когда размеры площадки стремятся к нулю, а сама площадка стягивается в точку: 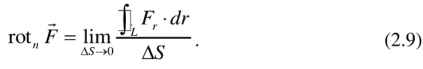 При этом направление обхода контура выбирается так, чтобы, если смотреть в направлении п, контур L обходился по часовой стрелке. В трехмерной декартовой системе координат ротор вычисляется следующим образом: 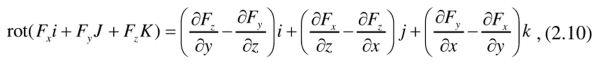 где i,j и к- единичные орты (векторы) для осейх,у иz соответственно. Для удобства представления можно условно представлять ротор в матричном виде как векторное произведение, формально представляющее векторное произведение как определитель: 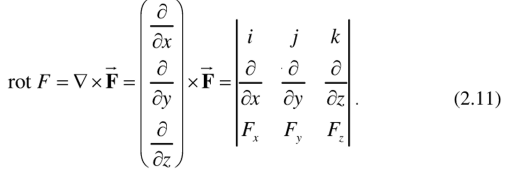 Основные свойства ротора: 1) - это векторная величина, которая является дифференциальной (т.е. точечной) характеристикой векторного поля . 2) Дивергенция ротора векторного поля равна нулю: т.е. поле не имеет источников. При этом верно и обратное: если поле F бездивергентно, оно есть поле ротора некоторого потенциального поля G: 3) Если поле F потенциально, то его ротор равен нулю в любой точке поля, т.е. поле F является безвихревым: Верно и обратное: если поле безвихревое, то оно потенциально для некоторого скалярного поля 20.Потенциальное поле, условие потенциальности. Условие независимости криволинейного интеграла от формы пути интегрирования. Векторное поле является потенциальным, если оно представляет собой поле градиентов некоторого скалярного поля . Функцию называют потенциальной функцией или просто потенциалом. Работа потенциального векторного поля по перемещению материальной точки из точки в точку не зависит от траектории её движения и выражается следующим криволинейным интегралом 2-го рода: Иными словами, в потенциальном поле имеет значение лишь начальная и конечная точка маршрута. И если эти точки совпадают, то суммарная работа сил по замкнутому контуру будет равна нулю: Векторное поле A назывется потенциальным, если его можно представить в виде градиента некоторого скалярного поля : Само скалярное поле называется при этом потенциалом векторного поля A. Иначе говоря, векторное поле A является потенциальным, если координаты вектора A можно представить в виде частных производных некоторого скаляного поля : 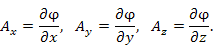 Условия потенциальности поля. Пусть Рассмотрим скалярное произведение векторов A и dr: 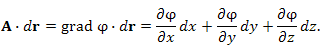 Выражение в правой части этого равенства представляет собой полный дифференциал функции . Если частные производные 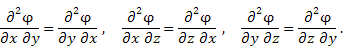 Учитывая, что частные производные от функции являются координатами вектора A, получаем следующие условия потенциальности поля A: 19 вопрос Понятие функции нескольких переменных (ФНП). 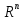 – множество упорядоченных действительных чисел ( – множество упорядоченных действительных чисел (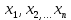 ) )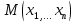 – точки пространства – точки пространства 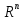 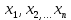 – координаты точки – координаты точкиОпределение  Если в каждой точки 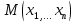 из некоторого множества D ( из некоторого множества D (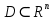 ) поставлено в соответствие по некоторому закону число u (единственное), то говорят, что на множестве D определена функция переменных u = f( ) поставлено в соответствие по некоторому закону число u (единственное), то говорят, что на множестве D определена функция переменных u = f(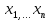 ) или u = f(M). ) или u = f(M).D = область определения функции Определение Пусть D – множество точек плоскости OXY. Если каждой точке 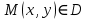 поставлено в соответствии по некоторому закон f число z, то говорят, что задана функция двух переменных z = f(x, y). поставлено в соответствии по некоторому закон f число z, то говорят, что задана функция двух переменных z = f(x, y).График функции z = f(x, y) поверхность в пространстве. 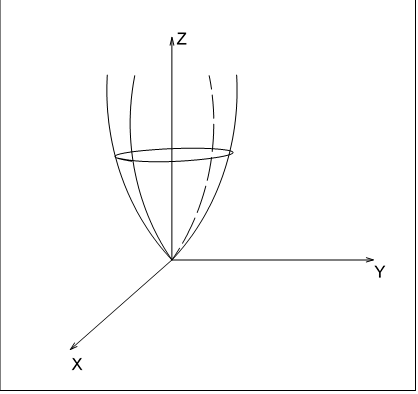 Линия уровня - кривые на которых z = f(x, y) принимает одно и тоже значение. f(x, y) = const. Определение Пусть  . Если каждой точки M(x, y, z) по некоторому закону f поставлено в соответствие число u, то говорят, что задана функция 3-ёх переменных f(x, y, z) = const. . Если каждой точки M(x, y, z) по некоторому закону f поставлено в соответствие число u, то говорят, что задана функция 3-ёх переменных f(x, y, z) = const.Определение 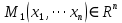 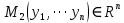 Расстояние 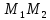 – число – число 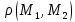 = = 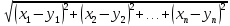 Определение 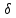 - окрестностью точки - окрестностью точки 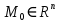 называется множество точек называется множество точек 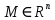 , для которых , для которых 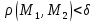 . .Определение частных производных. Определение Частной производной ФНП в точке 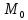 по переменной по переменной  называется предел отношения частного приращения по называется предел отношения частного приращения по  функции к функции к 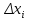 , когда , когда 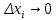 и обозначается и обозначается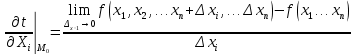 Для функции 2-ух переменных z = f(x, y), M(x, y) 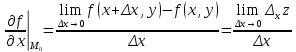 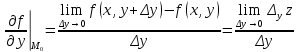 Геометрический смысл частных производных 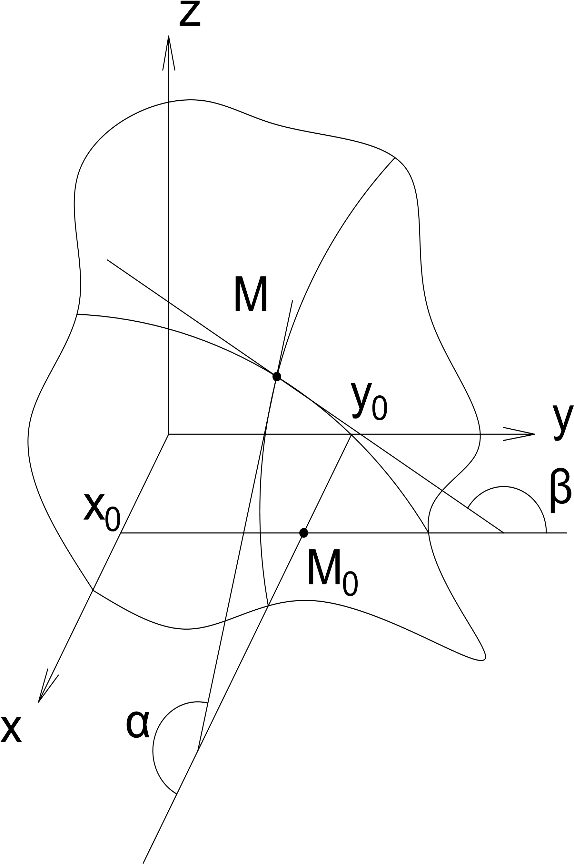  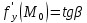 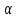 – угол между OX и касательной в точке – угол между OX и касательной в точке 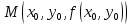 к линии пересечения поверхности z = = f(x, y) и плоскости y = к линии пересечения поверхности z = = f(x, y) и плоскости y = 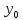 (аналогично (аналогично 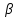 … x = … x = 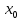 ) )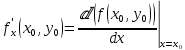 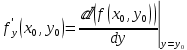 Т.е. частная производная в точке равна производной функции одного аргумента, вычисленного про соответствующем значении аргумента, поэтому при нахождении частной производной пользуются обычными правилами вычисления производных. |
