солянка матеша. солянка из матеши. Определенный интеграл от функции по отрезку это предел интегральных сумм при. Геометрический смысл определенного интеграла заключается в том, что его значением является площадь криволинейной трапеции для непрерывной и неотрицательной функции вида расположенной на интервале.
 Скачать 6.87 Mb. Скачать 6.87 Mb.
|
16Криволинейный интеграл I родаПусть на плоскости Оху задана непрерывная кривая АВ (или L) длины l. Рассмотрим непрерывную функцию f(x; у), определенную в точках дуги АВ. Разобьем кривую АВ точками   Ее называют интегральной суммой для функции f(x;y) по кривой АВ. Пусть 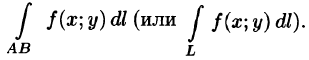 Таким образом, по определению,  Условие существования криволинейного интеграла I рода (существования предела интегральной суммы (55.1) при Теорема 55.1. Если функция f(х; у) непрерывна в каждой точке гладкой кривой (в каждой точке Аналогичным образом вводится понятие криволинейного интеграла от функции f(х; у; z) по пространственной кривой L. Приведем основные свойства криволинейного интеграла по длине дуги (I рода). 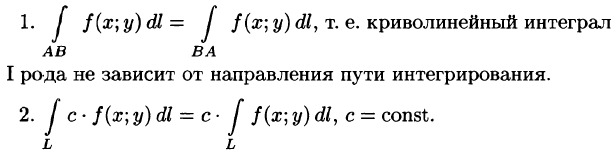 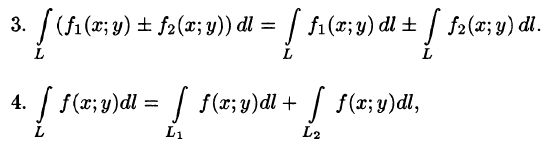 если путь интегрирования L разбит на части 5. Если для точек кривой L выполнено неравенство 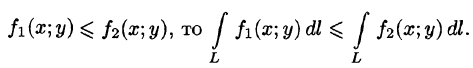 6. 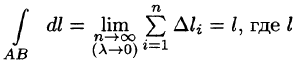 — длина кривой AB — длина кривой AB7. Если функция f(x; у) непрерывна на кривой АВ, то на этой кривой найдется точка 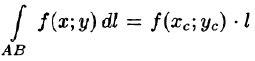 (теорема о среднем). (теорема о среднем). |
