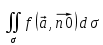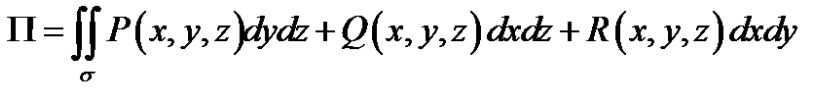При введении понятия определённого интеграла 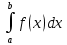 предполагалось, что выполняются следующие два условия: предполагалось, что выполняются следующие два условия:
а) пределы интегрирования а и b являются конечными;
б) подынтегральная функция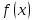 ограничена на отрезке [a,b] . ограничена на отрезке [a,b] .
Если хотя бы одно из этих условий не выполняется, то интеграл называется несобственным.
Определение. Пусть функция 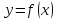 определена и непрерывна на промежутке [a,+∞), тогда определена и непрерывна на промежутке [a,+∞), тогда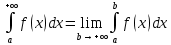 называется несобственным интегралом с бесконечным верхним пределом интегрирования (несобственным интегралом I рода). Если называется несобственным интегралом с бесконечным верхним пределом интегрирования (несобственным интегралом I рода). Если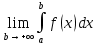 существует и конечен, то несобственный интеграл существует и конечен, то несобственный интеграл 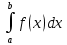 называется сходящимся; если данный предел не существует или равен ±∞ , то несобственный интеграл называется расходящимся. называется сходящимся; если данный предел не существует или равен ±∞ , то несобственный интеграл называется расходящимся.
Теорема 1(1-й признак сравнения)
Пусть 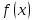 и и 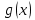 определены и непрерывны определены и непрерывны 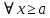 и при этом и при этом
0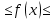 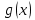 , тогда если , тогда если 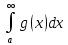 – сход, то и – сход, то и 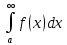 сход. И наоборот сход. И наоборот
Теорема 2(2-й признак сравнения)
Пусть 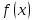 и и 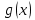 - непрерывны и положительны на [a,+∞),и пусть существует конечный предел - непрерывны и положительны на [a,+∞),и пусть существует конечный предел 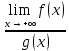 =A =A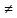 0, тогда интегралы 0, тогда интегралы 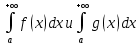 сходится и расходится одновременно. сходится и расходится одновременно.
6) Двойной интеграл и его геометрический смысл. Свойства двойного интеграла
Двойной интеграл от неотрицательной функции f(x;y)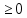 численно равен объему тела, которое сверху ограничено поверхностью z=f(x;y), снизу – замкнутой областью D плоскости Oxy, с боков – цилиндрической поверхностью, образующая которой параллельна оси Oz , а направляющей служит граница D , т.е. численно равен объему тела, которое сверху ограничено поверхностью z=f(x;y), снизу – замкнутой областью D плоскости Oxy, с боков – цилиндрической поверхностью, образующая которой параллельна оси Oz , а направляющей служит граница D , т.е.
V= 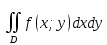
Свойства:
Линейность. f1=f1(x,y) f2=f2(x,y) 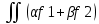 dT= dT=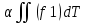 + +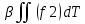
Если  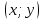  D и D и 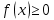 , то , то 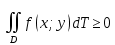
Если  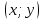  D и f1(x,y) D и f1(x,y)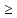 f2(x,y) f2(x,y) 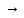 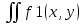 dT dT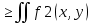 dT dT
Если f(x,y) =1, ∬DdT то равен площади этой области S(D)
Если область D является объединением двух областей D 1 и D 2, то 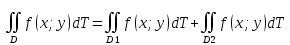
Теорема о среднем. Если функция 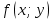 непрерывна на области D, то существует точка P ∈ D,такая что непрерывна на области D, то существует точка P ∈ D,такая что  f(P)*S(D); S(D)-площадь области D f(P)*S(D); S(D)-площадь области D
7) Замена переменной в двойном интеграле. Якобиан. ДИ в полярных координатах
Замена переменной в интеграле 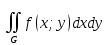 состоит в переходе от переменных x и y к новым переменным u и v, связанных соотношениями состоит в переходе от переменных x и y к новым переменным u и v, связанных соотношениями
x= X (u, v), y = Y (u,v), (u,v) D. (3.4)
При выполнении условий, что отображение (3.4) взаимно однозначно, а функции в соотношении (3.4) непрерывно-дифференцируемы, то якобиан отображения – определитель, составленный из первых частных производных:
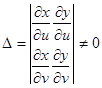 Обычно замена переменных производится с целью упрощения области интегрирования. Соотношения (3.4) называют переходом от прямоугольных декартовых координат к криволинейным. Примером криволинейных координат являются полярные координаты, связанные с прямоугольными формулами: x =rcos Обычно замена переменных производится с целью упрощения области интегрирования. Соотношения (3.4) называют переходом от прямоугольных декартовых координат к криволинейным. Примером криволинейных координат являются полярные координаты, связанные с прямоугольными формулами: x =rcos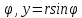 ; r = ; r = 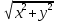

8) Тройной интеграл в сферических и цилиндрических координатах. Вывод якобиана
Переход от прямоугольных координат x, y, z к цилиндрическим координатам r,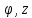 , связанным с x,y, z соотношениями x =rcos , связанным с x,y, z соотношениями x =rcos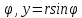 , z =z , z =z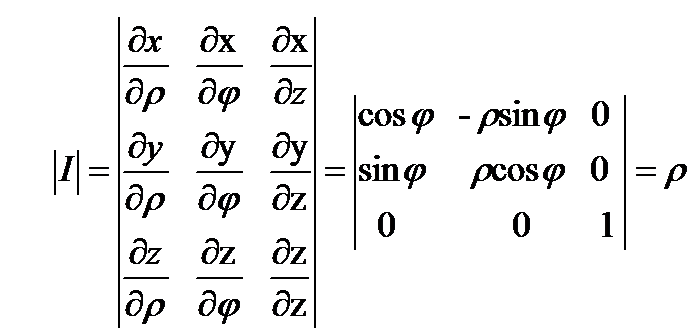
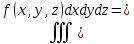 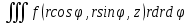 dz dz
Переход от прямоугольных координат x, y, z к сферическим координатам r,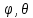 , связанным с x, y, z соотношениями x= , связанным с x, y, z соотношениями x=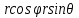 , y=r , y=r 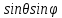 ,z=r ,z=r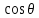
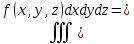 
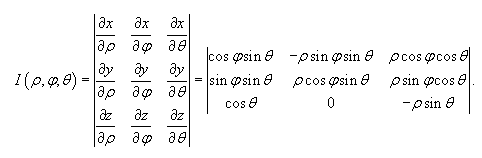 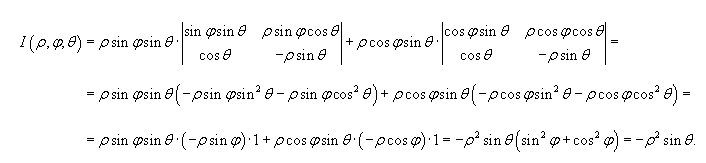
9) Поверхностный интеграл первого рода и его свойства
Определение. Поверхностным интегралом первого рода от функции f(P) по поверхности Ω называется предел интегральных сумм при , если этот предел существует и не зависит ни от способа разбиения поверхности Ω на частичные области Ω1 , ни от выбора в каждой из них точки P(i) если этот предел существует и не зависит ни от способа разбиения поверхности Ω на частичные области Ω1 , ни от выбора в каждой из них точки P(i) Ωi: Ωi: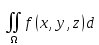 Ω= Ω=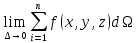
Свойство 1. Постоянный множитель можно выносить за знак интеграла
Свойство 2. Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций
Свойство 3. Если поверхность разбить на две поверхности и , то интеграл по всей поверхности будет равен сумме интегралов по поверхностям и
Свойство 4 (Теорема о среднем). Если функция непрерывна вдоль гладкой поверхности , то на этой поверхности существует такая точка , что справедлива формула
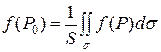
Свойство 5. При изменении стороны поверхности интегрирования величина интеграла не изменяется:
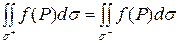 ,где и – стороны поверхности интегрирования . ,где и – стороны поверхности интегрирования .
10) Поток векторного поля через поверхность, его физический смысл. Свойство потока, его вычисление
Определение. Потоком вектора  через поверхность σ называется поверхностный интеграл от скалярного произведения вектора поля на нормальный единичный вектор к поверхности: через поверхность σ называется поверхностный интеграл от скалярного произведения вектора поля на нормальный единичный вектор к поверхности:
Flow=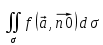
Поток можно записать в координатной форме, вычислив скалярное произведение векторов
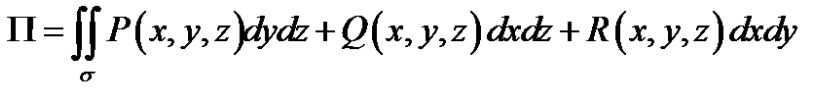
Физический смысл потока: если вектор-функция F есть поле скоростей текущей жидкости, то поток П этого векторного поля через поверхность S общему количеству жидкости, протекающей через S за единицу времени. 
Билет 13
Пусть в области задано некоторое векторное поле F i j k, где 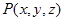 , ,  , , 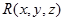 – непрерывно дифференцируемые в области функции. Пусть – гладкая ориентируемая поверхность, на которой выбрана определенная сторона, задаваемая единичной нормалью n – непрерывно дифференцируемые в области функции. Пусть – гладкая ориентируемая поверхность, на которой выбрана определенная сторона, задаваемая единичной нормалью n 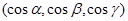 к этой поверхности. к этой поверхности.
Потоком векторного поля F через поверхность S в направлении единичной нормали n называют поверхностный интеграл первого рода:
П 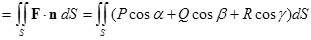 . .
|
(1)
|
Поверхностный интеграл первого рода в формуле (1) связан с поверхностным интегралом второго рода равенством:
П 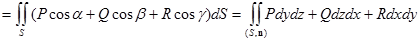 , ,
|
(2)
|
которое дает еще один способ вычисления потока.
Физический смысл потока: если вектор-функция F есть поле скоростей текущей жидкости, то поток П этого векторного поля через поверхность S общему количеству жидкости, протекающей через S за единицу времени.

Билет 14
Формула Гаусса—Остроградского.
Теорема. Пусть векторное поле  непрерывно дифференцируемо в замыкании элементарной области непрерывно дифференцируемо в замыкании элементарной области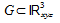 , граница которой , граница которой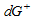 является кусочно-гладкой поверхностью, ориентированной полем внешних нормалей. Тогда справедлива формула Гаусса-Остроградского является кусочно-гладкой поверхностью, ориентированной полем внешних нормалей. Тогда справедлива формула Гаусса-Остроградского 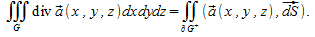 (1) (1)
Доказательство. Формулу Гаусса-Остроградского, опуская аргументы, можно представить в виде 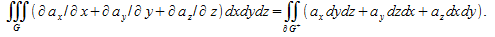 (2) (2)
Докажем равенство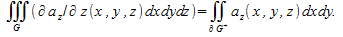 (3) (3)
В силу элементарности области G относительно оси z существует измеримое множество 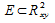 и функции и функции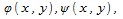 непрерывные на замыкании множества E и такие, что непрерывные на замыкании множества E и такие, что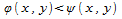 для любых для любых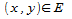 и и 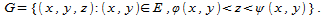
Поэтому поверхность «криволинейного цилиндра» G состоит из трёх частей:
«верхнего основания» 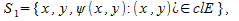 «нижнего основания» «нижнего основания» 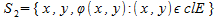 и «боковой поверхности» и «боковой поверхности» 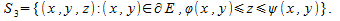
Поскольку вектор нормали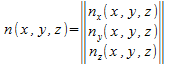 к «боковой поверхности» к «боковой поверхности»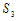 параллелен плоскости xy, то параллелен плоскости xy, то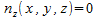 при при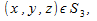 следовательно, сводя интеграл второго рода к интегралу первого рода, получаем следовательно, сводя интеграл второго рода к интегралу первого рода, получаем 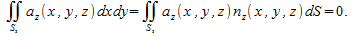
Пользуясь определением 2 для поверхностных интегралов второго рода по верхней стороне поверхности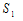 и нижней стороне поверхности и нижней стороне поверхности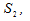 получаем получаем 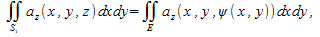 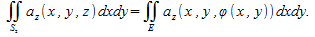
Следовательно,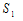 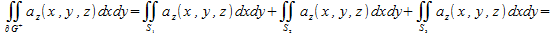 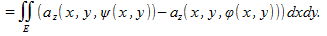
Пользуясь формулой Ньютона-Лейбница, получаем 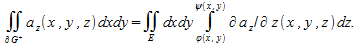
Отсюда и из теоремы о сведении кратного интеграла к повторному следует формула (3).
Аналогично, пользуясь элементарностью области G относительно осей x и y, можно получить равенства 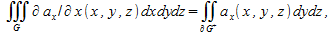 (4) (4) 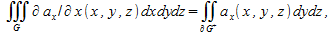 (5) (5)
Складывая равенства (3)-(5), получаем формулу Гаусса-Остроградского (2).
15
Дивергенция векторного поля и ее физический смысл
Математически дивергенция - это дифференциальный оператор divF, отображающий векторное поле на скалярное поле, т.е. осуществляющий операцию дифференцирования, в результате применения которой к векторному полю получается скалярное поле. Этот оператор определяет для каждой точки поля насколько расходятся входящий и исходящий потоки. Дивергенция векторного поля F определяется выражением

где Фр — поток векторного поля F через любую поверхность площадью S, ограничивающую объем V, при условии, что поверхность находится внутри сферы радиусом, стремящимся к нулю.
Если векторное поле дифференцируемо в некоторой области, тогда в трехмерном декартовом пространстве дивергенция будет определяться выражением
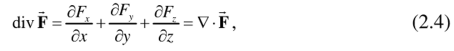
где V - векторный дифференциальный оператор набла.
Физический смысл дивергенции векторного поля состоит в том, что эта характеристика показывает то, в какой степени данная точка пространства является источником или стоком этого поля:
- если div F > 0, тогда точка поля является источником (истоком);
- если div F < 0, тогда точка поля является стоком;
- если divF = 0, тогда стоков и источников нет, либо они компенсируют друг друга.
|
 Скачать 6.87 Mb.
Скачать 6.87 Mb.
 непрерывно дифференцируемо в замыкании элементарной области
непрерывно дифференцируемо в замыкании элементарной области к «боковой поверхности»
к «боковой поверхности»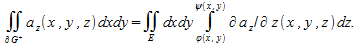

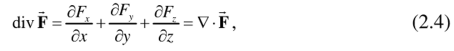

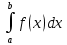 предполагалось, что выполняются следующие два условия:
предполагалось, что выполняются следующие два условия: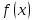 ограничена на отрезке [a,b] .
ограничена на отрезке [a,b] . 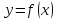 определена и непрерывна на промежутке [a,+∞), тогда
определена и непрерывна на промежутке [a,+∞), тогда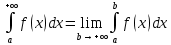 называется несобственным интегралом с бесконечным верхним пределом интегрирования (несобственным интегралом I рода). Если
называется несобственным интегралом с бесконечным верхним пределом интегрирования (несобственным интегралом I рода). Если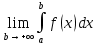 существует и конечен, то несобственный интеграл
существует и конечен, то несобственный интеграл  определены и непрерывны
определены и непрерывны 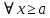 и при этом
и при этом 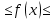
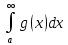 – сход, то и
– сход, то и 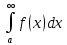 сход. И наоборот
сход. И наоборот 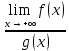 =A
=A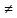 0, тогда интегралы
0, тогда интегралы 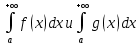 сходится и расходится одновременно.
сходится и расходится одновременно.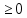 численно равен объему тела, которое сверху ограничено поверхностью z=f(x;y), снизу – замкнутой областью D плоскости Oxy, с боков –
численно равен объему тела, которое сверху ограничено поверхностью z=f(x;y), снизу – замкнутой областью D плоскости Oxy, с боков – 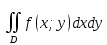
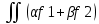 dT=
dT=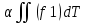 +
+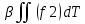

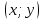
 D и
D и 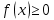 , то
, то 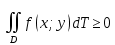
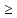 f2(x,y)
f2(x,y) 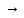
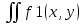 dT
dT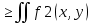 dT
dT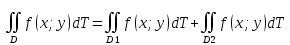
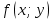

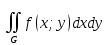 состоит в переходе от переменных x и y к новым переменным u и v, связанных соотношениями
состоит в переходе от переменных x и y к новым переменным u и v, связанных соотношениями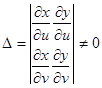 Обычно замена переменных производится с целью упрощения области интегрирования. Соотношения (3.4) называют переходом от прямоугольных декартовых координат к криволинейным. Примером криволинейных координат являются полярные координаты, связанные с прямоугольными формулами: x =rcos
Обычно замена переменных производится с целью упрощения области интегрирования. Соотношения (3.4) называют переходом от прямоугольных декартовых координат к криволинейным. Примером криволинейных координат являются полярные координаты, связанные с прямоугольными формулами: x =rcos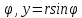 ; r =
; r = 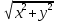
 , связанным с x,y, z соотношениями x =rcos
, связанным с x,y, z соотношениями x =rcos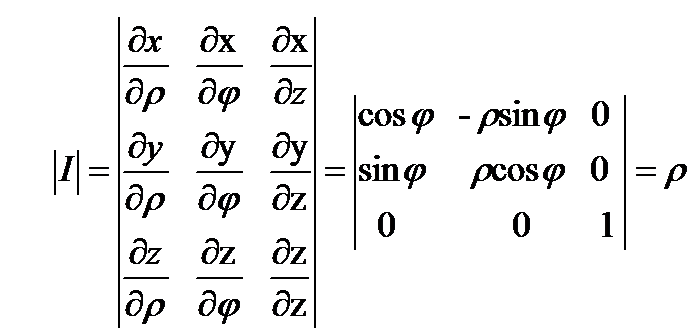
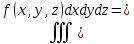
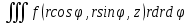 dz
dz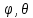 , связанным с x, y, z соотношениями x=
, связанным с x, y, z соотношениями x=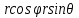 , y=r
, y=r 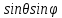 ,z=r
,z=r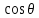

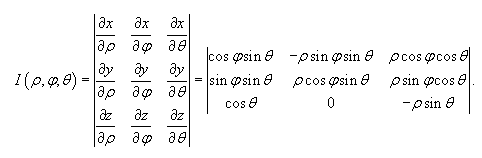
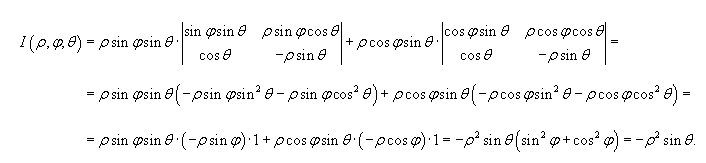
 если этот предел существует и не зависит ни от способа разбиения поверхности Ω на частичные области Ω1 , ни от выбора в каждой из них точки P(i)
если этот предел существует и не зависит ни от способа разбиения поверхности Ω на частичные области Ω1 , ни от выбора в каждой из них точки P(i)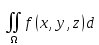 Ω=
Ω=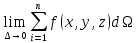
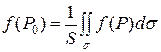
 через поверхность σ называется поверхностный интеграл от скалярного произведения вектора поля на нормальный единичный вектор к поверхности:
через поверхность σ называется поверхностный интеграл от скалярного произведения вектора поля на нормальный единичный вектор к поверхности: