солянка матеша. солянка из матеши. Определенный интеграл от функции по отрезку это предел интегральных сумм при. Геометрический смысл определенного интеграла заключается в том, что его значением является площадь криволинейной трапеции для непрерывной и неотрицательной функции вида расположенной на интервале.
 Скачать 6.87 Mb. Скачать 6.87 Mb.
|
|
20 вопрос Дифференцируемость функции нескольких переменных. Полный дифференциал. Определение Пусть функция z = f(x, y) определена в некоторой окрестности точки 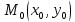 . .Функция z = f(x, y) называется дифференцируемой в точке 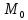 , если её полное приращение , если её полное приращение 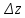 можно представить в виде можно представить в виде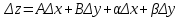 А и В некоторые константы, не зависящие от 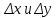 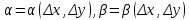 – бесконечно малые функции при – бесконечно малые функции при 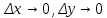 Определение Линейная (относительно 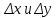 ) часть приращения функции ) часть приращения функции 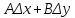 называется полным дифференциалом и обозначается называется полным дифференциалом и обозначается 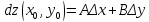 или или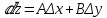  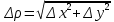 – расстояние между – расстояние между 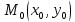 и и 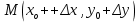 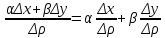 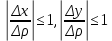 (ограничены) (ограничены)Тогда 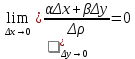 , т.е. , т.е. 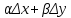 = = 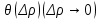 , тогда , тогда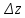 можно записать в виде можно записать в виде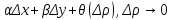 Теорема 1 (необходимое условие дифференцируемости) Если f(x, y) дифференцируема в точке 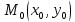 , то она непрерывна в этой точке. , то она непрерывна в этой точке.Доказательство: f – дифференцируема 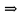 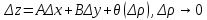   непрерывна в точке непрерывна в точке 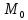 Теорема 2 (необходимое условие дифференцируемости) Если f(x, y) дифференцируема в точке 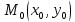 , то она имеет частные производные в этой точке. , то она имеет частные производные в этой точке.Доказательство: 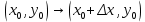 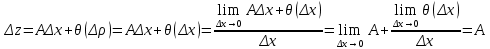 Аналогично 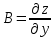 . .Теорема 3 (достаточное условие дифференцируемости) Если функция z = f(x, y) имеет частные производные в точке 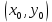 , непрерывные в этой точке, то она дифференцируема. , непрерывные в этой точке, то она дифференцируема.Доказательство: Пусть f(x, y) = z имеет непрерывные частные производные 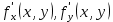 в точке в точке 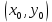 . .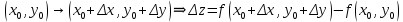 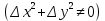 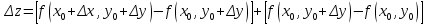 Рассмотрим функцию 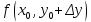 на [ на [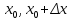 ] ( ] (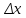 > 0) и на [ > 0) и на [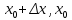 ] ( ] (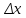 < 0). < 0).Тогда 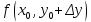 удовлетворяет условиям теоремы Лагранжа. удовлетворяет условиям теоремы Лагранжа.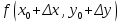 - - 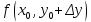 = = 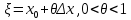 Так как частное производное 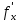 в точке в точке 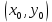 непрерывна, то непрерывна, то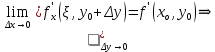 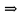 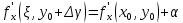 , где , где  при при 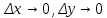 Тогда получаем 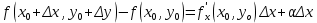 Аналогично, по формуле Лагранжа для функции f(x, y) на 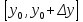 ( (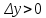 ) и на ) и на 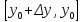 ( (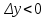 ). ).Получаем 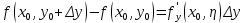 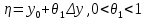 Так как 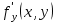 непрерывна, то аналогично действию выше получаем непрерывна, то аналогично действию выше получаем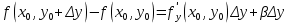 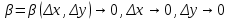 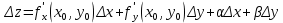 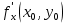 = A, = A, 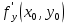 = B – const, не зависящие от = B – const, не зависящие от 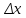 и и 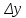 . .Ч.Т.Д 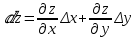 21 вопрос Производная по направлению. Пусть задана функция u = u(x, y, z), определённая и дифференцируема в некоторой окрестности точки 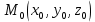 . Рассмотрим вектор . Рассмотрим вектор  , где , где 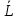 образует с координатными осями углы α, β, γ; точка образует с координатными осями углы α, β, γ; точка 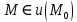 , , 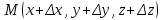 ( (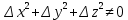 ). ).Тогда полное приращение функции 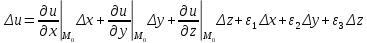 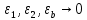 при при 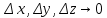 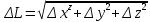 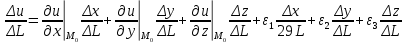 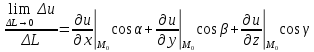 (1) (1)Определение Если существует предел (1) при 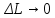 , то он называется производной функции , то он называется производной функции 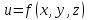 в точке в точке 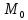 по направлению по направлению 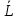 и обозначается и обозначается 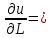 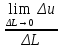 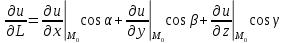 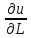 не зависит от длины вектора L, а зависит только от направления не зависит от длины вектора L, а зависит только от направления 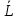 . .Градиент скалярного поля Если в каждой точке пространства определенно значение некоторой величины, то говорят, что в данной области задано поле этой величины. Если величина скалярная, то поле называется скалярным, в случае векторной величины – векторным полем. z = f(x, y) – плоское скалярное поле Скалярное поле задаётся функцией u = f(M). Определение Вектор 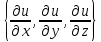 называется градиентом скалярного поля u = u(x, y, z) в точке (x, y, z) и обозначается называется градиентом скалярного поля u = u(x, y, z) в точке (x, y, z) и обозначается 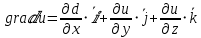 Вопрос 22 Экстремум функции двух переменных. Необходимое условие. Достаточные условия экстремума. Пусть определена в некоторой окрестности точки 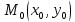 . .Определение Точка 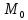 называется точкой локального максимума (минимума), если существует окрестность этой точки, в которой называется точкой локального максимума (минимума), если существует окрестность этой точки, в которой 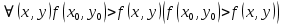 . .Точки max и min называются точками экстремума, 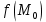 -- экстремумом. -- экстремумом.Теорема 1 (необходимое условие экстремума) Если в точке 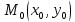 функция z = f(x, y) имеет экстремум, то её частное производное в точке функция z = f(x, y) имеет экстремум, то её частное производное в точке 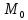 равно 0 или не существует. равно 0 или не существует.Доказательство: Пусть 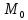 – точка экстремума функции z = f(x, y) – точка экстремума функции z = f(x, y)Предположим, что это точка max, тогда в некоторой окрестности 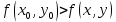 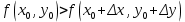 Зафиксируем 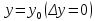 , получаем функцию одного аргумента , получаем функцию одного аргумента 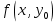 . Эта функция по определению имеет max в точке . Эта функция по определению имеет max в точке 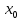 , тогда , тогда 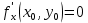 или или 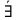 . .Аналогично по переменной y (фиксируем x = 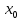 … ) … )Если точка 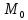 – точка min, то доказательство аналогичное. – точка min, то доказательство аналогичное.Ч.Т.Д. Определение Точка 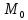 – называется точкой max (min), если существует окрестность этой точки, в которой – называется точкой max (min), если существует окрестность этой точки, в которой 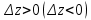 . .Теорема 2 (достаточное условие экстремума) Пусть функция f(x, y) имеет непрерывные частные производные до 2-го порядка, включительно, в некоторой окрестности точки 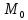 . Если в точке . Если в точке 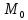 частные производные равны 0, а частные производные равны 0, а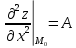 , , 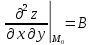 , , 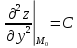 , то , топри 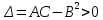 точка точка 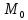 является точкой экстремума, причём, если А < 0, то является точкой экстремума, причём, если А < 0, то 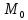 – точка max, если А > 0, то – точка max, если А > 0, то 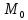 – точка min, – точка min,при 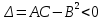 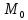 не является точкой экстремума. не является точкой экстремума.Доказательство: Формула Тейлора при n = 1 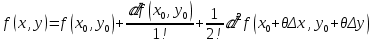 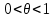 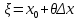  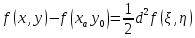  Так как частные производные 2-го порядка – непрерывны. 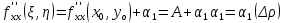 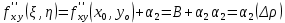 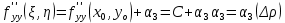  при при 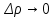 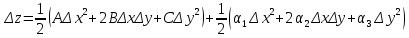 Пусть 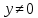 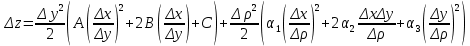 При достаточно малом 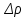 знак правой части последнего равенства совпадает со знаком квадратного трёхчлена. знак правой части последнего равенства совпадает со знаком квадратного трёхчлена.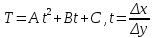 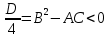 , то Т имеет постоянный знак , то Т имеет постоянный знакПри А < 0 – Т < 0; При А > 0 – T >0 Если 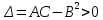 и А < 0, то и А < 0, то 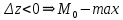 А > 0, то 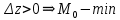 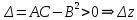 меняет знак, следовательно меняет знак, следовательно 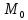 не является точкой экстремума. не является точкой экстремума.Ч.Т.Д. 25. БИЛЕТ: Обыкновенные дифференциальные уравнения. Решение дифференциального уравнения. Общее и частное решение. Формулировка теоремы о существовании и единственности решения задачи Коши для дифференциального уравнения первого порядка.   26. БИЛЕТ:Линейные однородные и неоднородные дифференциальные уравнения n-го порядка. Структура общего решения(одна теорема с доказательством).   27. БИЛЕТ: Линейные однородные дифференциальные уравнения n-го порядка с постоянным коэффициентами. Фундаментальная система решений. Метод Эйлера.    28. БИЛЕТ: Линейные неоднородные дифференциальные уравнения n-го порядка с постоянными коэффициентами. Теорема о структуре решения. Метод подбора частного решения.    |
