стерио. "Оптическая изомерия"

• Название: "Оптическая изомерия"
• Дата: 29.04.2019
• Размер: 225.15 Kb.
• Имя файла: стерио.docx
• Тип: Литература; #75685
• страница: 2 из 3

1.2 в. Корпускулярная теория

В настоящее время возрождается интерес к корпускулярной теории света, которой придерживался еще Ньютон. Частицей света является фотон - реальная элементарная частица. В фотонной теории поляризацию света связывают с поляризацией фотонов, которая обусловлена наличием у этих частиц спина и его определенной направленностью в пространстве. Спиновые квантовые числа - это как бы дополнительные внутренние степени свободы частицы. В отличие от электронов, имеющих спин J = 1/2, спин фотона J = 1. (Это означает, что электроны принадлежат к классу фермионов, для которых справедлив запрет Паули, а фотоны - к классу бозонов, для которых не действует принцип запрета). Согласно квантовой механике, частица со спином J и ненулевой массой покоя имеет (2J + 1) внутренних квантовых состояний, определяющих ее поляризацию, т.е. степень асимметрии частицы в пространстве. Но масса покоя фотона равна нулю, и поэтому число спиновых состояний на единицу меньше, т.е. равно двум (+1 и - 1). Это означает, что возможны лишь две ориентации проекции спина фотона на направление его движения: параллельная и антипараллельная. В таком случае возникает понятие "спиральность частицы". Если проекция спина на направление движения положительна, то говорят, что частица имеет правовинтовую (правую) спиральность, а если отрицательна - левовинтовую (левую) спиральность. Спиральные объекты хиральны, поэтому фотоны являются как бы хиральными частицами.

Поскольку фотоны обладают целочисленным спином, в одном и том же состоянии может находится любое число фотонов. Это обусловливает возможность описания электромагнитных взаимодействий с участием большого числа фотонов в рамках классической (а не только квантовой) механики. Циркулярно-поляризованный свет можно рассматривать как поток фотонов, имеющих только правую или только левую спиральность. Плоскополяризованный свет состоит из одинакового количества "левых" и "правых" фотонов. Взаимодействие по-разному поляризованных фотонов с хиральной анизотропной средой происходит неодинаково, что приводит к хироптическим эффектам.

Ахиральная молекула не вращает плоскость поляризации света только при определенной ее ориентации по отношению к падающему лучу. Например, ахиральная молекула, имеющая плоскость симметрии, не вращает плоскость поляризации лишь в том случае, если плоскость поляризации совпадает с плоскостью симметрии. Все же остальные молекулы, не ориентированные таким образом, вращают плоскость поляризации, даже не будучи хиральными. Однако в целом образец не вращает, так как в массе молекулы ориентированы беспорядочно, и одни молекулы вращают плоскость поляризации в одном направлении, а другие молекулы, встречающиеся на пути светового луча, вращают ее в противоположную сторону. Таким образом коллектив ахиральных молекул имеет суммарное вращение, равное нулю, хотя каждая молекула может вращать плоскость поляризации. В случае хиральных соединений молекул противоположной ориентации (если это не рацемическая смесь) просто не может существовать, и вращение наблюдается.

2. Хиральные молекулы

В случае простых молекул легко проводится зрительное распознавание несовместимости с зеркальным отображением. Однако многие органические молекулы настолько сложны, что такой способ требует очень развитого пространственного воображения, которым обладают далеко не все.

2.1 Точечные группы симметрии

Шар самый симметричный объект, его не возможно отразить в зеркале. Он всегда выглядит одинаково. Тетраэдр "менее симметричен", чем шар, поскольку вокруг высоты его нужно повернуть лишь на определенный угол (1200), чтобы он выглядел так же, как до поворота. Вращение вокруг оси является одной из операций симметрии. Операцией симметрии называется действие над объектом, которое приводит к его новой ориентации, неотличимой от исходной и совмещаемой с нею.

Каждой операции симметрии соответствует определенный элемент симметрии. Элементом симметрии называется геометрическое место точек, остающихся неподвижными при данной операции симметрии. Основными элементами симметрии являются собственные оси вращения, которые в системе обозначений Шенфлиса имеют символ Cn, где n - порядок оси, означающий, что поворот молекулы на угол 2p /n радиан приводит к структуре, неотличимой от первоначальной, несобственные оси вращения или зеркально-поворотные оси (s n), зеркальные плоскости симметрии (s), делящие молекулу пополам, так, что одна половина является зеркально-симметричной другой половине, центр инверсии (i) и тождественное преобразование (Е). В соответствии с этим операции симметрии делят на поворот оси вокруг оси симметрии Сn, поворот вокруг оси с последующим отражением в плоскости, перпендикулярной этой оси (Sn), отражение в плоскости симметрии s, инверсию в центре симметрии i и операцию идентичности Е. При операции идентичности с молекулой ничего не делают, но эта операция не бессмысленна, т.к. она позволяет включить в единую классификацию как симметричные, так и асимметричные объекты.

2.1 а. Собственная ось симметрии

Все молекулы имеют тривиальную ось С1, поскольку в любом случае вращение на 3600 возвращает молекулу в исходное состояние. Следовательно, операция С1 эквивалентна операции идентичности (С1 є Е). Дихлорметан имеет ось С2, аммиак - ось С3, метан - четыре оси С3, тетрахлорплатинат - ось С4.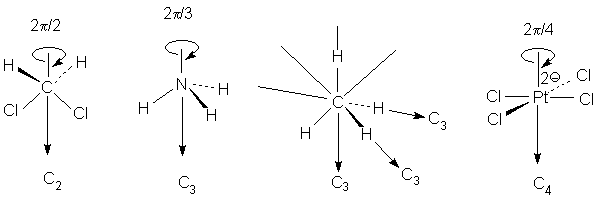



2.1 б. Несобственная ось симметрии

Простейшая зеркально поворотная ось S1 эквивалентна перпендикулярной ей плоскости симметрии (S1 є s). Примером является молекула хлорфторметана. Зеркально-поворотные оси более высокого порядка (Sn) можно рассматривать как комбинацию вращения на угол 2p /n с последующим отражением в плоскости, перпендикулярной оси вращения. Так, аллен и изображенный ниже изомер 1,2,3,4-тетраметилциклобутана имеет зеркально-поворотную ось S4: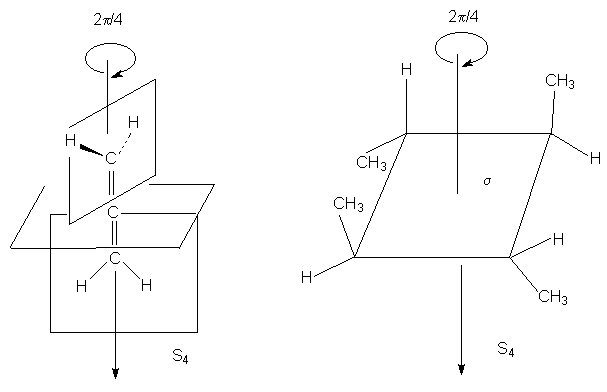



1,2-Дихлор-1,2-дифторэтан обладает осью S2, которая совпадает со связью С-С. Операция S2 эквивалентна инверсии в центр симметрии, который находится посредине связи С-С (S2 є i)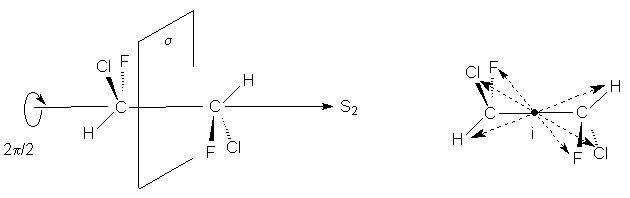



Поскольку у молекул может быть не один, а несколько элементов симметрии, их удобнее классифицировать по точечной группе симметрии. Набор все операций симметрии объекта образует его группу симметрии. Если при всех этих преобразованиях остается неподвижным центр тяжести фигуры, то группа симметрии называется точечной. Известны четыре типа точечных групп симметрии.

2.1 в. Типы точечных групп симметрии

К типу 1 относятся точечные группы С1, Сs, Ci, которые не имеют нетривиальных поворотных осей, поэтому их называют неаксиальными. К типу 2 относятся группы с единственной поворотной осью. В группе Cn других элементов симметрии нет, в группе Cnv имеется n вертикальных плоскостей s n, проходящих через ось Cn, а в группе Сnh одна горизонтальная плоскость s h, перпендикулярная оси Сn. Сюда же входит группа Sn, поскольку при наличии зеркально-поворотной оси порядка n обязательно имеется и собственная ось порядка n/2 (C2 у S4, C3 у S6 и т.д.). При нечетном n оси Sn могут быть представлены как комбинации других операций. Для низших порядков S1 є s и S2 є i. Точечные группы типа 3 имеют одну ось Сn и n осей второго порядка, перпендикулярных оси Сn. Такие группы называются диэдральными. Если нет плоскостей симметрии, группа обозначается как Dn, если имеется несколько плоскостей s v (вертикальных) - Dnd, а если еще и горизонтальная плоскость s h, то группа обозначается Dnh. К типу 4 относятся точечные группы, имеющие более чем одну ось порядка выше двух. Такие группы называются кубическими. К ним относятся точечные группы правильных тетраэдра (Td), октаэдра и куба (Oh), икосаэдра и додекаэдра (Ih). Максимальную симметрию имеет шар, который принадлежит предельной группе Kh, включающей все возможные операции симметрии.

2.2 Симметричное определение хиральности

Хиральна любая истинно асимметрическая молекула, относящаяся к группе С1, не имеющая никаких элементов симметрии, кроме идентичности (и оси С1, т.к. С1 Е). Очевидно, также, что молекулы, имеющие плоскость симметрии (s) или центр симметрии (i) ахиральны, поскольку они состоят из двух одинаковых "половинок" и в зеркальном отображении левая и правая половинки преобразуются друг в друга или без поворотов (при наличии плоскости), или с поворотом на 1800 (при наличии центра инверсии). Молекулы, имеющие зеркально-поворотные оси (Sn) также совмещаются со своим зеркальным отображением, и поэтому ахиральны. Следовательно, хиральны только молекулы, относящиеся к аксиальным точечным группам Сn и Dn.

Таким образом, можно сформулировать симметрийный критерий хиральности: любая молекула, которая не имеет несобственной оси вращения Sn хиральна.

Впервые доказательство справедливости данного определения хиральных молекул получено при исследовании изомерных четвертичных аммонийных солей со спирановым атомом азота IV, V, VII и IX. Изомеры IV и V асимметричны (группа C1), изомер VII диссимметричен (группа D2). Поэтому эти три изомера должны быть хиральными. И действительно, они были получены в оптически активной форме. Однако изомер VIII относится к группе S4, т.е. ахирален, и получить его в оптически активной форме нельзя.

2.3 Типы хиральности

Молекулы, содержащие тетраэдрический атом, например, углерода с четырьмя разными заместителями принадлежат к точечной группе С1. Они асимметричны и центральный атом называется асимметрическим атомом.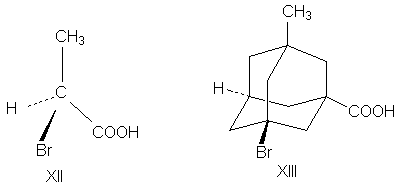



Адамантаны, у третичных атомов углерода которых имеется четыре разных заместителя, хиральны и оптически активны. При сравнении формул симметрия обоих соединений очень похожа. Остов адамантана можно представить как тетраэдр с "изломанными ребрами", он имеет симметрию Td которая переходит в C1, когда все четыре заместителя у третичных атомов углерода разные. У производного адамантана нет асимметрического атома углерода, как в a-бромпропионовой кислоте, но есть центр, находящийся внутри молекулы (центр тяжести незамещенного адамантана).

Асимметрический центр - это частный случай более общего понятия хиральный центр. Хиральный центр может иметь не только асимметрические молекулы, но и молекулы симметрии Cn или Dn. Хиральный центр является лишь одним из возможных элементов хиральности. Однако кроме центрального существуют еще и аксиальный, планарный и спиральный типы хиральности.

Аксиальной хиральностью обладают молекулы, имеющие хиральную ось. Хиральную ось легко получить, мысленно "растягивая" центр хиральности: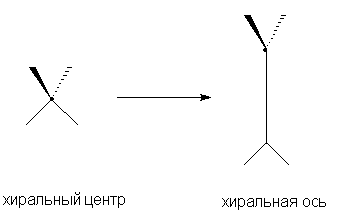



Хиральную ось имеют такие классы молекул, как аллены и дифенилы. В алленах центральный атом углерода sp-типа имеет две взаимно-перпендикулярные p-орбитали, каждая из которых перекрывается с p-орбиталью соседнего атома углерода, в результате чего остающиеся связи концевых атомов углерода располагаются в перпендикулярных плоскостях. Сам аллен хирален, так как имеет зеркально-поворотную ось S4, но несимметрично замещенные аллены типа abС=С=Сab хиральны.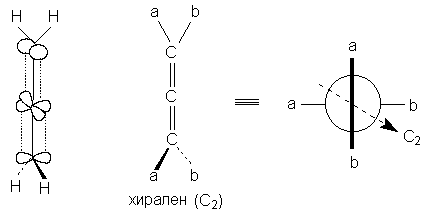



Аллены хиральны только в том случае, если оба концевых атома углерода замещены несимметрично: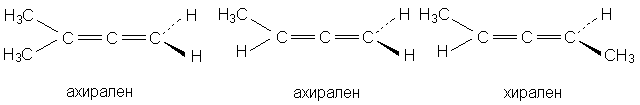



При любом нечетном числе кумулированных двойных связей четыре концевые группы располагаются уже не в разных, а в одной плоскости, например, для 1,2,3-бутатриена: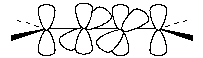



Такие молекулы ахиральны, но для них наблюдается цис-транс-изомерия.

Так, соединение было разделено на оптические изомеры.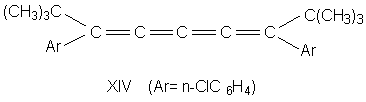



Если одну или обе двойные связи симметрично замещенного аллена заменить на циклическую систему, то полученные молекулы будут тоже обладать аксиальной хиральностью, например: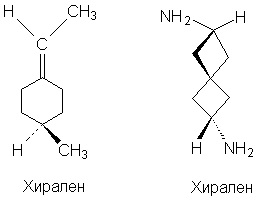



В бифенилах, содержащих четыре объемистые группы в орто-положениях, свободное вращение вокруг центральной связи затруднено из-за стерических препятствий, и поэтому два бензольных кольца не лежат в одной плоскости. По аналогии с алленами, если одно или оба бензольных кольца замещены симметрично, молекула ахиральна; хиральны же молекулы только с двумя несимметрично замещенными кольцами, например: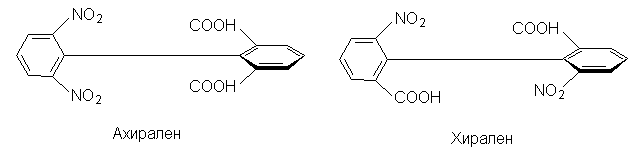



Изомеры, которые можно разделить только благодаря тому, что вращение вокруг простой связи затруднено, называются атропоизомерами.

Иногда для предотвращения свободного вращения в бифенилах достаточно трех и даже двух объемистых заместителей в орто-положениях. Так, удалось разделить на энантиомеры бифенил-2,2-дисульфокислоту (XV). В соединении XVI свободное вращение полностью не заторможено, и, хотя его можно получить в оптически активной форме, при растворении в этаноле оно быстро рацемизуется (наполовину за 9 мин. при 250).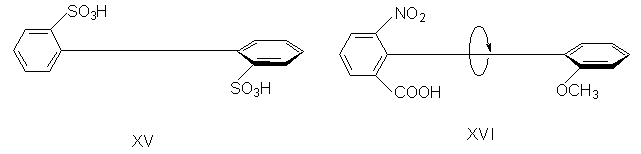



Для некоторых хиральных молекул определяющим структурным элементом является не центр, не ось, а плоскость. Простейшую модель планарной хиральности легко сконструировать из любой плоской фигуры, не имеющей осей симметрии, лежащих в этой плоскости, и отдельной точки вне плоскости. Наиболее изучены планарно-хиральные производные ферроцена (XVII). Другими примерами являются ареновые комплексы хромтрикарбонила (XVIII), а также соединения XIX и XX.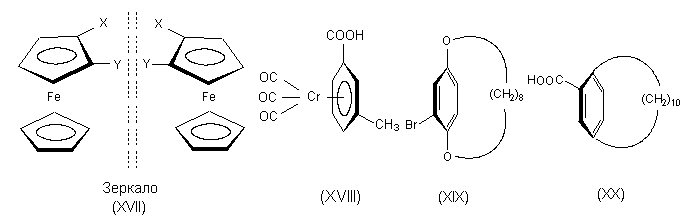



Спиральная хиральность обусловлена спиральной формой молекулы. Спираль может быть закручена влево или вправо, давая энантиомерные спирали. Например, в гексагелицене одна часть молекулы из-за пространственных препятствий вынуждена располагаться над другой.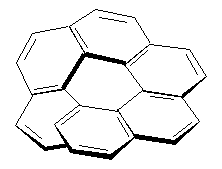



3.Номенклатура энантиомеров

Определение конфигурации-это экспериментальная работа, выполняемая химическими и физическими методами с целью установить, какая из двух зеркальных пространственных моделей отвечает правовращающему энантиомеру, а какая - левовращающему. При полной определенности самой конфигурации (пространственной модели) вопрос об ее обозначении может решаться по-разному.

3.1 По конфигурации: R - и S

Система R/S - наиболее важная номенклатурная система для характеристики энантиомеров. По этой системе, центр хиральности называется R или S в соответствии с системой, по которой каждое замещающее звено наделяется приоритетом в соответствии с правилами Кана-Инголда-Прелога, основываясь на атомном номере. Если центр ориентирован так, что низший из возможных четырёх направлен от наблюдателя, наблюдатель увидит два возможных варианта: если приоритет оставшихся трёх замещающих групп уменьшается по часовой стрелке, название даётся R (Rectus), если уменьшается против часовой стрелки, то S (Sinister). Эта система маркирует каждый хиральный центр молекулы (и также имеет распространение на хиральные молекулы, не затрагивая хиральных центров). Несмотря на это, она более обобщённа, чем система D/L, и может, например, наименовать изомер, в котором (R,R) - группа расположена напротив (R,S) - диастереомер. У системы R/S нет отношения к (+/-) - системе. R-изомер может быть правоповоротным, так и левоповоротным, в зависимости от фактических замещающих групп. У системы R/S нет и отношения к D/L системе. По этой причине система D/L остаётся в повседневном использовании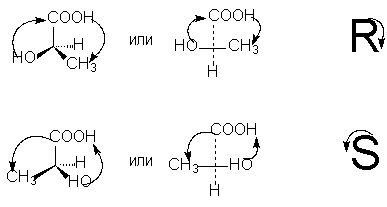



3.2 По оптической активности: +/-

Энантиомер именуется по направлению света, в котором вращает плоскость поляризованного света. Если вращение происходит по часовой стрелке (по отношению к наблюдателю, к которому направляется свет), то в названии энантиомера отмечается (+). Его зеркальный образ именуется (-). (+) - и (-) - изомеры также определяются как D - и L соответственно (от англ. Dextrorotatory - правоповоротный и Levorotatory - левоповоротный).

3.3 По конфигурации: D - и L-

Оптический изомер может быть назван по пространственной конфигурации его атомов. Система D/L делает это, опираясь на молекулу глицераля. Сам по себе глицераль хирален, и два его изомера именуются D и L. С глицералем можно провести определённые химические манипуляции без изменения конфигурации, и его историческое использование с этой целью (в совокупности с удобством его использования как одной из наименьших широко используемых хиральных молекул) вылилось в его использование в номенклатуре. В этой системе составные части называются по аналогии с глицералем, который, в общем, производит недвусмысленные обозначения, да к тому же и легче всего увидеть в маленьких биомолекулах, похожих на глицераль. Маркировка D/L не относится к (+) / (-) никаким образом; она не указывает, какой энантиомер правоповоротный, какой - левоповоротный. Однако она сообщает, что стереохимия соединений имеет отношение к тому, что из право - или левоповоротного энантиомеров глицераля правоповоротный будет D-изомером. Общая закономерность для определения D/L изомерии аминокислот называется правилом “CORN”. Группы COOH, R, NH3 и H (где R - отличная от других углеродная цепь) выстраиваются вокруг атома углерода хирального центра. Когда смотреть так, чтобы атом водорода был направлен вдаль от наблюдателя, если эти группы расположены по часовой стрелке вокруг атома углерода, то это D-форма. Если против часовой, то L-форма.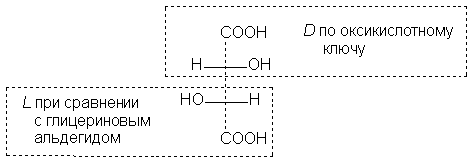