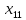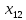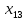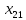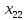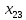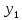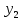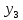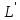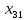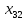РГР по ТПР(1). Оптимизация целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях
 Скачать 29.33 Kb. Скачать 29.33 Kb.
|
|
Содержание ВведениеВ настоящее время оптимизация находит применение в науке, технике и в любой другой области человеческой деятельности. Оптимизация — целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях. Поиски оптимальных решений привели к созданию специальных математических методов и уже в XVIII веке были заложены математические основы оптимизации (вариационное исчисление, численные методы и др). Однако до второй половины XX века методы оптимизации во многих областях науки и техники применялись очень редко, поскольку практическое использование математических методов оптимизации требовало огромной вычислительной работы, которую без ЭВМ реализовать было крайне трудно, а в ряде случаев - невозможно. Постановка задачи оптимизации предполагает существование конкурирующих свойств процесса, например: количество продукции - расход сырья, количество продукции - качество продукции. Выбор компромиссного варианта для указанных свойств и представляет собой процедуру решения оптимизационной задачи. Критерием оптимальности называется количественная оценка оптимизируемого качества объекта. На основании выбранного критерия оптимальности составляется целевая функция, представляющая собой зависимость критерия оптимальности от параметров, влияющих на ее значение. Вид критерия оптимальности или целевой функции определяется конкретной задачей оптимизации. Таким образом, задача оптимизации сводится к нахождению экстремума целевой функции. В зависимости от своей постановки, любая из задач оптимизации может решаться различными методами, и наоборот – любой метод может применяться для решения многих задач. Линейное программирование - один из первых и наиболее подробно изученных разделов математического программирования. Именно линейное программирование явилось тем разделом, с которого начала развиваться сама дисциплина «математическое программирование». Можно сказать, что линейное программирование применимо для построения математических моделей тех процессов, в основу которых может быть положена гипотеза линейного представления реального мира: экономических задач, задач управления и планирования, оптимального размещения оборудования и пр. Задачами линейного программирования называются задачи, в которых линейны как целевая функция, так и ограничения в виде равенств и неравенств. Кратко задачу линейного программирования можно сформулировать следующим образом: найти вектор значений переменных, доставляющих экстремум линейной целевой функции при m ограничениях в виде линейных равенств или неравенств. Линейное программирование представляет собой наиболее часто используемый метод оптимизации. К числу задач линейного программирования можно отнести задачи: рационального использования сырья и материалов; задачи оптимизации раскроя; оптимизации производственной программы предприятий; оптимального размещения и концентрации производства; составления оптимального плана перевозок, работы транспорта; управления производственными запасами; и многие другие, принадлежащие сфере оптимального планирования. В настоящее время линейное программирование является одним из наиболее употребительных аппаратов математической теории оптимального принятия решения. Для решения задач линейного программирования разработано сложное программное обеспечение, дающее возможность эффективно и надежно решать практические задачи больших объемов. Эти программы и системы снабжены развитыми системами подготовки исходных данных, средствами их анализа и представления полученных результатов. Современные методы линейного программирования достаточно надежно решают задачи общего вида с несколькими тысячами ограничений и десятками тысяч переменных. Для решения сверхбольших задач используются уже, как правило, специализированные методы. Построение математической модели Цель оптимизации: максимизация прибыли производства костюмов при выполнении установленного производственного плана производства. Составим математическую модель. Введем переменные данной задачи: i - вид костюма( i=1..3) j – номер цеха (j=1..3) Пусть xij – количество костюмов i-го вида, производимых на j-ом цехе Ci – стоимость одного костюма i-го вида aij - издержки от производства одного i-го костюма в j-ом цехе bj – мощность производства j-го цеха Составим ограничения, которым должны удовлетворять эти переменные. Количество произведенных костюмов на j-ом цехе не должно превышать мощности цеха: 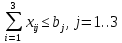 Данная задача относится к классу задач целочисленного линейного программирования, поэтому 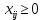 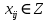 Эти ограничения означают, что отрицательное количество костюмов не имеет содержательного смысла, также как и дробное число костюмов. Составим целевую функцию, которая в математической форме, отражает критерий эффективности выбора лучшего варианта. Так как необходимо составить оптимальный план производства, дающий максимальную прибыль, то максимальная прибыль будет получена от произведения произведенного количества костюмов на их стоимость минус издержки производства этих костюмов: 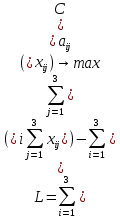 Итак, математическая модель будет иметь вид: 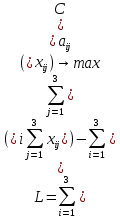 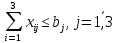 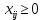 , (i= , (i=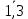 , j= , j=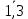 ) )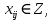 (i= (i=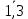 , j= , j=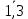 ) )Математическая модель: 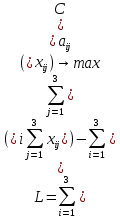 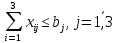 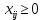 , (i= , (i=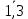 , j= , j=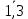 ) )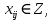 (i= (i=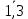 , j= , j=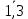 ) )Рассмотрим пример: Пусть 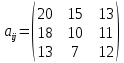 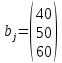 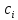 = =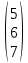 Тогда 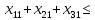 40 40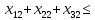 50 50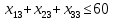 Задача в специальной форме: 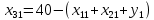 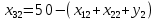 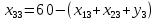 После преобразований получим следующую целевую функцию: 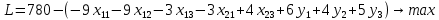 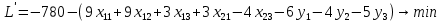 Решим задачу симплекс-методом. Составим симплекс-таблицу: 
Соответственно получаем: 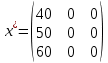 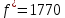 |