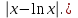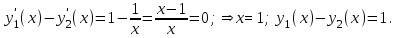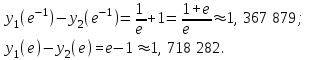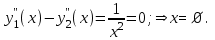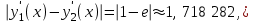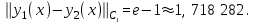Оптимизация в автоматизированных системах управления
 Скачать 1.35 Mb. Скачать 1.35 Mb.
|
2.2. Выполнение заданийЗадание 1. Рассмотрите пример. Найти расстояние в классе функций C0 и C1 (близких в смысле близости нулевого и первого порядков, соответственно) между функциями y1(x)=x и y2(x)=lnx на отрезке x  [e−1, e]. [e−1, e]. Для вычисления расстояния в классе C0 используем формулу
Чтобы вычислить максимальную по модулю разность между двумя функциями, воспользуемся обычными приёмами нахождения наибольшего значения функции на отрезке. Найдём все экстремумы функции y1(x)−y2(x) в интервале x  (e−1, e), затем вычислим значения этой функции на краях интервала и выберем наибольшее по модулю значение − это и будет расстояние между y1(x) и y2(x) в C0. Исследуем на экстремум: (e−1, e), затем вычислим значения этой функции на краях интервала и выберем наибольшее по модулю значение − это и будет расстояние между y1(x) и y2(x) в C0. Исследуем на экстремум:
Значения функции y1(x)−y2(x) на краях интервала x  (e−1, e): (e−1, e):
Из трёх вычисленных значений функции (они все положительные) выбираем максимальное − это и есть расстояние между функциями в C0:
Нарисуйте с помощью MATLAB [4 – 6] графики функций y1(x) и y2(x) (прил.). Опишите функции в виде символических выражений, так как дальше необходимо будет построить графики их производных: clear all % очистили всё syms x % символический аргумент y1=x; % описали функции y2=log(x); xpl=linspace(exp(-1),exp(1)); % массив для графика y1pl=subs(y1,x,xpl); % вычислили функции y2pl=subs(y2,x,xpl); plot(xpl,y1pl,'-b',xpl,y2pl,'-r') % рисуем set(get(gcf,'CurrentAxes'),... 'FontName','Times New Roman Cyr','FontSize',12) title(['\bfГрафики функций '... '\rm\ity\rm_1(\itx\rm) и \ity\rm_2(\itx\rm)']) xlabel('\itx') % метка оси OX ylabel('\ity\rm_1(\itx\rm), \ity\rm_2(\itx\rm)') da=daspect; % получили масштаб da(1:2)=min(da(1:2)); % уравняли daspect(da); % установили xlim([exp(-1) exp(1)]); % пределы по оси OX. 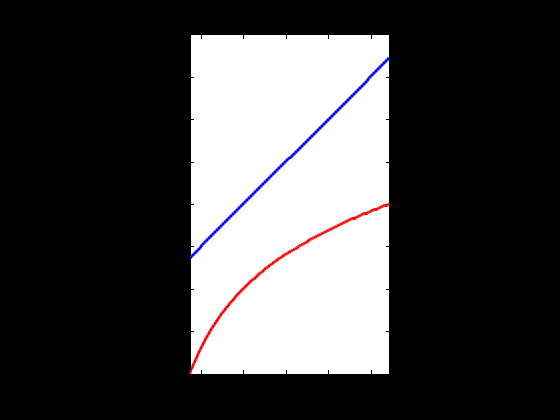 На полученных графиках видно, что, действительно, максимальная по модулю разность между функциями y1(x)=x и y1(x)=lnx на интервале x  [e−1,e] достигается на правом краю интервала при x=e. [e−1,e] достигается на правом краю интервала при x=e. Теперь надо найти расстояние между функциями в C1. Максимальная по модулю разность между значениями функции получена – это (9). Надо найти максимальную по модулю разность между производными. Экстремумы внутри интервала [e−1, e]:
Значения на концах интервала:
Максимальная по модулю разность между производными:
расстояние между y1(x) и y1(x) в C1 − это максимальная из величин (9)и (12):
Проверьте этот результат с помощью MATLAB: нарисуйте графики производных рассматриваемых функций. Дифференцирование провести аналитически, с помощью команды diff. Далее выполнить те же действия, что и в предыдущей зоне ввода: подставить значения аргументов, нарисовать график, подписать заголовок и метки осей, уравнять масштабы и установить границы по оси Ox. Dy1=diff(y1,'x') % вычисляем производные Dy2=diff(y2,'x') Dy1pl=subs(Dy1,x,xpl); % подставляем аргументы Dy2pl=subs(Dy2,x,xpl); figure % новая фигура plot(xpl,Dy1pl,'-b',xpl,Dy2pl,'-r') % рисуем set(get(gcf,'CurrentAxes'),... 'FontName','Times New Roman Cyr','FontSize',12) title(['\bfГрафики функций '... '\rm\ity\rm''_1(\itx\rm) и \ity\rm''_2(\itx\rm)']) xlabel('\itx') % метка оси OX ylabel('\ity\rm''_1(\itx\rm), \ity\rm''_2(\itx\rm)') da=daspect; % получили масштаб da(1:2)=min(da(1:2)); % уравняли daspect(da); % установили xlim([exp(-1) exp(1)]); % пределы по оси OX 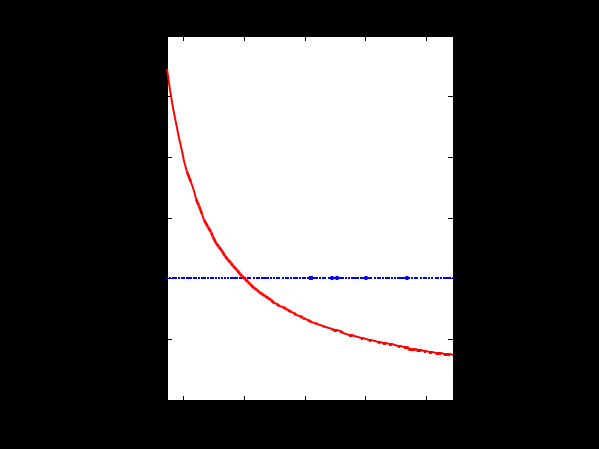 На графиках видно, что максимальная по модулю разность значений производных достигается на левом краю интервала при 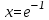 . . Задание 2. Установить, близки ли в смысле близости нулевого и первого порядков кривые 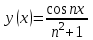 и и 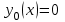 на отрезке на отрезке 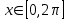 при при 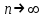 . Проверить результат с помощью MATLAB: нарисовать графики функций и их производных. . Проверить результат с помощью MATLAB: нарисовать графики функций и их производных.Задание 3. Установить, близки ли в смысле близости нулевого и первого порядков кривые 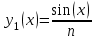 и и 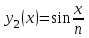 к функции к функции 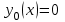 на отрезке на отрезке 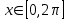 при при 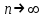 . Проверить результат с помощью MATLAB: нарисовать графики функций и их производных. . Проверить результат с помощью MATLAB: нарисовать графики функций и их производных. |