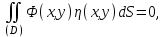Оптимизация в автоматизированных системах управления
 Скачать 1.35 Mb. Скачать 1.35 Mb.
|
Контрольные вопросыВ чём состоит основная задача вариационного исчисления? Какое утверждение правильное: C0  C1 или C1 C1 или C1 C0? C0? Если на функции y(x) достигается сильный экстремум, то достигается ли слабый? А если достигается слабый, то достигается ли сильный? 3. ОСНОВНАЯ ЛЕММА ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ 1. Лемма ЛагранжаВажную роль в вариационном исчислении играет лемма Лагранжа, которая называется основной леммой вариационного исчисления. Она используется при выводе дифференциальных уравнений Эйлера. Сформулируем и докажем эту лемму для функции одной переменной. Лемма. Если 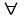 η(x) η(x) Ck на [x1, x2] интеграл от произведения этой функции на другую функцию Φ(x) Ck на [x1, x2] интеграл от произведения этой функции на другую функцию Φ(x)  Ck по [x1, x2] равен нулю: Ck по [x1, x2] равен нулю:
то это возможно только в том случае, если Φ(x)≡0 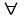 x x [x1, x2]. [x1, x2]. Доказательство. Проведём доказательство от противного. Пусть в какой-либо точке x0  [x1, x2]: Φ(x0)≠0. Для определённости будем считать, что Φ(x0)=A>0. Свойством функции, непрерывной на интервале, является то, что если непрерывная функция в какой-то точке x0 отлична от нуля, то существует некоторая малая окрестность этой точки, в которой функция тоже отлична от нуля и имеет тот же знак, что и в точке x0. В нашем случае Φ(x) [x1, x2]: Φ(x0)≠0. Для определённости будем считать, что Φ(x0)=A>0. Свойством функции, непрерывной на интервале, является то, что если непрерывная функция в какой-то точке x0 отлична от нуля, то существует некоторая малая окрестность этой точки, в которой функция тоже отлична от нуля и имеет тот же знак, что и в точке x0. В нашем случае Φ(x)  Ck, то есть является непрерывной. Поэтому существует некоторый интервал [x−, x+], в котором Φ(x)>0. Ck, то есть является непрерывной. Поэтому существует некоторый интервал [x−, x+], в котором Φ(x)>0. Покажем теперь, как можно построить такую функцию η(x)  Ck, что (1) будет нарушаться. Возьмём η(x) в виде Ck, что (1) будет нарушаться. Возьмём η(x) в виде
За счёт показателя n можно добиться дифференцируемости нужное число раз, а за счёт k − сделать функцию сколь угодно большой или малой. Тогда (1) будет нарушаться:
Так как каждый из сомножителей под интегралом положительный. Аналогично, если в какой-либо точке Φ(x0)<0, то для этой же η(x) интеграл (3) будет отрицательный. Отсюда по принципу от противного следует, что, если 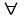 η(x) будет выполняться (1), то это возможно, только если Φ(x)≡0. η(x) будет выполняться (1), то это возможно, только если Φ(x)≡0. Замечание. Основная лемма вариационного исчисления справедлива и для функции нескольких переменных. Сформулируем и докажем её для функции двух переменных. Формулируется она так: если 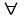 η(x,y) η(x,y)  Ck в области D Ck в области D
то это возможно только в том случае, если Φ(x,y)≡0 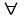 (x,y) (x,y)  D. D. Доказательство проводится так же, методом от противного. Предположим, что в какой-то точке (x0,y0)  D: Φ(x0,y0)=A>0. Значит, существует некоторая малая δ‑окрестность точки (x0,y0), в которой Φ(x0,y0)>0. Построим функцию η(x,y) в виде D: Φ(x0,y0)=A>0. Значит, существует некоторая малая δ‑окрестность точки (x0,y0), в которой Φ(x0,y0)>0. Построим функцию η(x,y) в виде
Для этой функции η(x,y) условие (4) будет нарушаться: подынтегральная функция будет отлична от нуля (причём положительна) только в δ -окрестности точки (x0,y0), поэтому интеграл (4) будет положительный. Аналогично, если в какой-то точке Φ(x0,y0) < 0, то для подобранной нами η(x,y) интеграл (4) будет отрицательный. Следовательно, добиться выполнения (4) при произвольной η(x,y) можно, только если Φ(x,y) ≡ 0. |