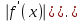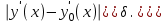Оптимизация в автоматизированных системах управления

• Название: Оптимизация в автоматизированных системах управления
• Дата: 11.05.2021
• Размер: 1.35 Mb.
• Имя файла: 33_38.docx
• Тип: Документы; #203420
• страница: 2 из 5

Контрольные вопросы

1. 
   Каким образом распределены по уровням функции управления в автоматизированных системах управления предприятием? Приведите примеры критериев оптимальности для разных уровней управления.
   
2. 
   Для подсистем какого уровня иерархии ставится задача динамической оптимизации? Для каких подсистем ставится задача статической оптимизации?
   
3. 
   Какого типа критерии качества автоматизированных систем называют скалярными?
   
4. 
   В каком случае при оптимизации процессов управления необходимо выбирать векторный критерий?
   
5. 
   Какие задачи оптимизации можно решать методами классического вариационного исчисления?
   

2. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ

2. 2.1. Введение в вариационное исчисление

Определение 1. Функционалом называется правило, по которому заданной функции y(t) из некоторого их множества ставится в соответствии число J.

Функционал обозначается J=J(y(t)). Множество функций y(t), на которых определен функционал J, называется классом функций.

Определение 2. Основной задачей вариационного исчисления является исследование на экстремум функционалов [1–3], то есть нахождение таких функций из данного класса, которые доставляют функционалу наибольшее или наименьшее значение. Такие функции называются экстремалями.

Определение 3. Классом функций C₀ на [a,b] называется множество функций, непрерывных на [a,b], для которых норма вычисляется по формуле

(1)

Две функцииy₀(t) иy(t) считаются близкимив классе C₀, если максимум модуля их разности мал:

(2)

где δ – малое число.

Определение 4. Близостью нулевого порядка называется близость в
смысле C_О.

Определение 5. Классом функций C₁ на [a,b] называется множество функций, дифференцирумых в [a,b], для которых норма вычисляется по формуле

(3)

Две функцииy₀(t) иy(t) считаются близкимив классе C₁, если малы расстояния между функциями и между их производными:

(4)

Определение 6. Близостью первого порядка называется близость в
смысле C₁.

Определение 7. Классом функций C_kна [a,b] называется множество функций, k раз дифференцирумых в [a,b], для которых норма вычисляется по формуле

((5)

Две функцииy₀(t) иy(t) считаются близкимив классе C_k, если малы расстояния между функциями и между их производными до k-го порядка включительно.

Определение 8. Близостью k-го порядка называется близость в смысле C_k.

Определение 9. Функция y₀(x) называется точкой минимума функционала J(y(x)), если 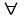y(x) из ее малой δ-окрестности выполняется условие J(y(x)) ≥ J(y₀(x)).

Определение 10. Функция y₀(x) называется точкой минимумаk-го порядкафункционала J(y(x)), если условие из определения 9 выполняется в δ-окрестности функции y₀(x) в C_k.

Определение 11. Экстремум нулевого порядка называется сильным. Экстремум первого порядка называется слабым (или слабым 1-го порядка). Экстремум k-го порядка называется слабым экстремумом k-го порядка. Если на какой-то функции достигается сильный экстремум, то достигается и слабый экстремум (любого порядка). Если на какой-то функции достигается слабый экстремум меньшего порядка, то достигается и слабый экстремум большего порядка.