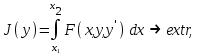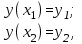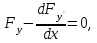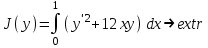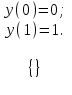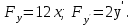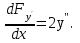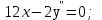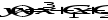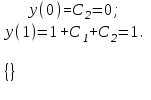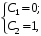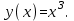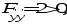Оптимизация в автоматизированных системах управления

• Название: Оптимизация в автоматизированных системах управления
• Дата: 11.05.2021
• Размер: 1.35 Mb.
• Имя файла: 33_38.docx
• Тип: Документы; #203420
• страница: 5 из 5

3.2. Выполнение заданий

Задание 1. Нарисуйте с помощью MATLAB пример функции η(x) C_k в соответствии с (2) для n = 2 и k =1 при x₋=0,4 и x₊₌0,6.

clear all % очистили всё

Xminus=0.4;

Xplus=0.6;

n=2;

k=1;

x=linspace(Xminus,Xplus);

y=k.*(x-Xminus).^(2*n).*(x-Xplus).^(2*n);

plot([0 x 1],[0 y 0]) % рисуем

set(get(gcf,'CurrentAxes'),...

'FontName','Times New Roman Cyr','FontSize',12)

title('\bfГрафик функции \rm\eta\rm(\itx\rm)')

xlabel('\itx') % метка оси OX

ylabel('\eta\rm(\itx\rm)') % метка оси OY

xlim([0 1]); % пределы по оси OX.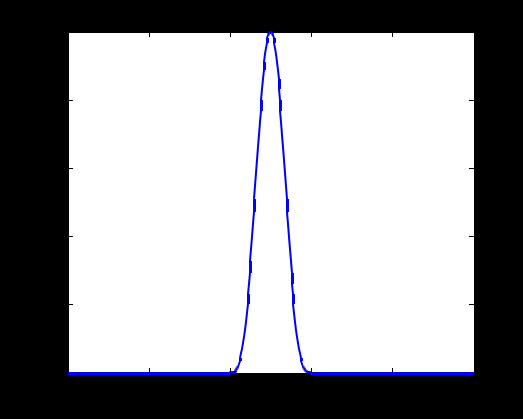



Задание 2. Нарисуйте трёхмерный график этой функции с помощью MATLAB для n =2 и k =1 при x₀=0,5, y₀=0,5, δ=0,2.

Чтобы вычислить функцию z на заданной сетке, надо провести вычисления по первой части формулы (5), а затем умножить поэлементно на булевский массив. При этом происходит автоматическое приведение типов, и булевский массив преобразуется в массив нулей и единиц. Таким образом, в области D вычисления проводятся по первой части (10), а вне D будет 0.

clear all % очистили всё

x0=0.5;

y0=0.5;

delta=0.2;

n=2;

k=1;

[X,Y]=meshgrid(linspace(0,1),linspace(0,1));

z=k.*((X-x0).^2+(Y-y0).^2-delta^2).^n.*...

((delta^2-(X-x0).^2-(Y-y0).^2)>0);

surf(X,Y,z) % рисуем

set(get(gcf,'CurrentAxes'),...

'FontName','Times New Roman Cyr','FontSize',12)

title(['\bfГрафик функции '...

'\rm\eta\rm(\itx\rm,\ity\rm)']) % заголовок

xlabel('\itx') % метка оси OX

ylabel('\ity') % метка оси OY

zlabel('\eta\rm(\itx\rm,\ity\rm)') % метка оси OZ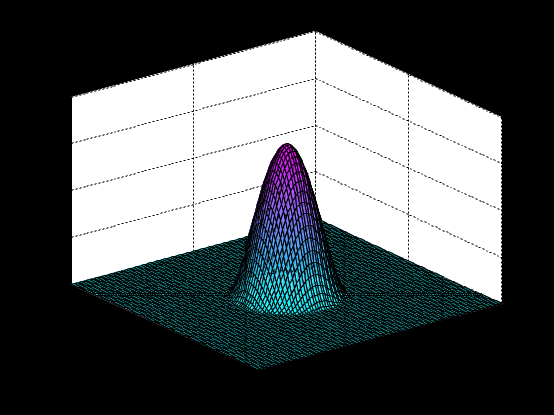

8. Контрольные вопросы

1. 
   Сформулируйте основную лемму вариационного исчисления и докажите её.
   

4. РЕШЕНИЕ ВАРИАЦИОННЫХ ЗАДАЧ С ИСПОЛЬЗОВАНИЕМ

ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ЭЙЛЕРА

9. 4.1. Дифференциальное уравнение Эйлера

Определение 1. Задача вариационного исчисления называется элементарной, если она формулируется следующим образом.

Задан функционал, зависящий от функции одной переменной y(t) и её производной y^’(t):

(1)

и граничные условия

(2)

где F(x,y,y^’) – непрерывная функция трех переменных и дифференцируемая функция двух своих последних аргументов.

Определение 2. Дифференциальным уравнением Эйлера называется уравнение

(3)

где F_y и F_y' – частные производные от F(x,y,y^’) по ее второму и третьему аргументам.

Определение 3. Любое решение задачи (3) с граничными условиями (2) называется экстремалью.

10. 4.2. Выполнение заданий

Задание 1. Рассмотрите пример.

Требуется найти экстремум функционала:

(4)

при граничных условиях

(5)

Решить пример аналитически. Найти частные производные F_y и F_y' от функции F(x,y,y^’) по второму и третьему аргументам:

(6)

Вычислить полную производную по x от F_y':

(7)

Составить дифференциальное уравнение Эйлера вида :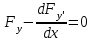

(8)

или после упрощений

(9)

Его общее решение имеет вид

(10)

Для нахождения произвольных постоянных C₁ и C₁ подставить решение (10) в граничные условия(5):

(11)

Видно, что система (11) имеет единственное решение. Решая эту систему, найти значения C₁ и C₂:

(12)

и тогда уравнение экстремали примет вид

(13)

По условию Лежандра, если на экстремали выполняется условие F_y'y' > 0, а на функциях, близких к экстремали, для произвольных y' имеет место F_y'y' ≥ 0, то достигается сильный минимум. В нашем случае это выполняется:

(14)

и, следовательно, на экстремали достигается сильный минимум.

Проверить этот результат: вычислить J(y) на нескольких функциях вида 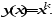Эти функции удовлетворяют граничным условиям (5) и, следовательно, являются допустимыми. Для вычислений применить MATLAB.

clear all % очистили всё

syms x % описали символический аргумент

k=1:5; % показатели степени

y=x.^k; % символические функции

Dy=diff(y,x); % производные

F=Dy.^2+12*x.*y; % подынтегральные функции

J=int(F,x,0,1); % функционалы

Jm=eval(J); % посчитали значения

disp('k J(x^k)') % печатаем заголовок

fprintf('%d %12.10f\n',[k;Jm]) % печатаем результаты

J(x^k)

1 5. 000 000 000 0

2 4. 333 333 333 3

3 4. 200 000 000 0

4 4. 285 714 285 7

5 4. 492 063 492 1

Убедитесь, что полученный результат не противоречит выводу о том, что на функции 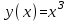достигается минимум. Проведенная проверка не доказывает этот факт, так как проверили только несколько из бесконечного числа функций, графики которых проходят через точки M₁(0,0) и M₂(1,1).

Доказать, применив необходимые условия экстремума функционала, что на экстремали достигается минимум.

Построить с помощью MATLAB график функции J(k).

Библиографический список

1. 
   Советов, Б.Я. Теоретические основы автоматизированного управления: учеб. для вузов / Б.Я. Советов, В.В. Цехановский, В.Д. Чертовской. − М.: Высш. школа, 2006.
   
2. 
   Куропаткин, П.В. Оптимальные и адаптивные системы: учеб. пособие для вузов / П.В. Куропаткин. − М.: Высш. школа, 1980.
   
3. 
   Краснов, Л.М. Вариационное исчисление / Л.М Краснов, Г.И. Макаренко, А.И. Киселев. − М.: Наука, 1973.
   
4. 
   Корн, Г. Справочник по математике для научных работников и инженеров / Г. Корн., Т. Корн. − М.: Наука, 1973.
   
5. 
   Иглин, С.П. Математические расчеты на базе MATLAB / С.П. Иглин. − СПб.: БВХ-Петербург, 2005.
   
6. 
   Дьяконов, В.П. MATLAB 6/6.1/6.5 + Simulink 4/5. Основы применения: полное руководство пользователя / В.П. Дьяконов. − М.: Солон-Пресс, 2002.
   
7. 
   Потемкин, В.Г. Система MATLAB: справ. пособие / В.Г. Потемкин. − М.: Диалог-МИФИ, 1998.
   

Приложение

элементы программирования на MATLAB

Рассмотрены элементы программирования на MATLAB, используемые для решения приведенных задач: символические вычисления, построение графиков, решение конечных и дифференциальных уравнений. Для более полного ознакомления с системой инженерных и научных расчетов MATLAB рекомендуется обратиться, например, к [5 – 7].

11. 1. Символические вычисления

Символические переменные описываются с помощью команды syms. Функция от символических переменных, построенная по обычным правилам, автоматически становится символической.

Для печати в MATLAB можно использовать два приёма.

1. 
   Не ставить точку с запятой в конце выражения при вычислении какой-либо величины. Точка с запятой подавляет вывод на экран.
   
2. 
   Использовать команды форматированной печати fprintf.
   

Команда fprintf не печатает непосредственно символические переменные. Для печати такую переменную нужно представить в виде строки символов. Преобразование любых типов в строку выполняется с помощью команды char.

Символическую функцию можно аналитически дифференцировать и интегрировать. Производные вычисляются с помощью команды diff.

Для интегрирования символических выражений используется функция int, которая позволяет вычислять и неопределённые, и определённые интегралы. Если пределы интегрирования не указаны, то вычисляется неопределённый интеграл, а если указаны – то определённый. Пределы могут быть константами или символическими переменными.

Вычисление значения символического выражения осуществляется с помощью функции eval.

Если строка с командой или оператором очень длинная, её можно перенести на следующую строку с помощью многоточия.

12. 2. Построение графиков

Простейший двумерный (2D) график можно построить с помощью команды plot. В этой команде нужно задать массивы абсцисс и ординат одинаковой длины. График будет построен по точкам и автоматически масштабирован.

Линейный массив аргументов на заданном интервале можно задать командой linspace. Этот массив нужно подставить в функцию вместо аргумента командой subs.

Для построения на одном графике нескольких функций нужно указать несколько массивов абсцисс и ординат.

После построения графика можно вручную оформить рисунок: написать заголовок (команда title), метки осей (команды xlabel и ylabel); отрегулировать масштаб (функция и команда daspect); установить пределы по координатным осям (команды xlim и ylim).

Трёхмерные (3D) графики рисуются так же. Вместо команды plot используются её 3D аналоги: команды plot3, mesh или surf. Они рисуют 3D графики в разных вариантах.

13. 3. Решение конечных уравнений

Для аналитического решения систем нелинейных уравнений служит команда solve. Уравнения задаются в виде символьных строк, а также символьной строкой задается список переменных, относительно которых нужно решить систему. Результат возвращается в виде массива символических переменных.

Для численного решения систем нелинейных уравнений в инструментарии для решения задач оптимизации Optimization Toolbox есть команда fsolve. При вызове команды fsolve информация о решаемой системе передается в виде функции, записанной в отдельный файл, озаглавленный так же, как называется функция (расширение дать *.m). Эта функция (написанная пользователем) по заданному вектору аргументов возвращает значения функций, которые должны обращаться в нуль.

14. 4. Решение дифференциальных уравнений

Для аналитического решения систем дифференциальных уравнений применятся команда dsolve. Она позволяет находить как общее, так и частное решение. Если начальные (или граничные) условия заданы, то команда находит частное решение, а если нет − то общее.

Сами дифференциальные уравнения, а также начальные или граничные условия должны быть заданы в виде строковых переменных. При этом применяются такие правила для обозначения производных: Dy – для первой производной; D2y − для второй; D3y − для третьей; и так далее, если y − искомая функция. Нужно указать, относительно какого аргумента решать уравнение. Результат возвращается в виде массива символических переменных. Длина массива − это количество найденных решений. Если искомых функций несколько, то каждый элемент массива является структурой, поля которой имеют такие же имена, как и искомые переменные.

Вывод строк для граничных условий осуществляется с помощью функции sprintf, которая выдаёт результат в строку.

Для численного решения систем дифференциальных уравнений в MATLAB существуют решатели дифференциальных уравнений: ode113, ode23, ode45 и др. Они применяются для разных систем (мягкие, жёсткие) и используют различные схемы численного интегрирования. Для них систему уравнений нужно привести к нормальному виду и задать начальные условия.

Преобразование типов от строки к символическому выражению создаётся командой sym. Обратная команда char применяется для преобразования символического выражения в строку.

СОДЕРЖАНИЕ

Предисловие 3

1. Критерии оптимальности автоматизированных систем управления 4

2. Основные понятия и определения вариационного исчисления 13

3. Основная лемма вариационного исчисления 19

4. Решение вариационных задач с использованием диффренциального

уравнения Эйлера 23

5. Исследование экстремалей функционалов 28

6. Решение вариационных задач в частных случаях уравнения Эйлера 34

7. Решение вариационных задач для функционалов с ограничениями 39

Библиографический список 46

Приложение. Элементы программирования на MATLAB 47