Оптимизация в автоматизированных системах управления
 Скачать 1.35 Mb. Скачать 1.35 Mb.
|
|
оптимизация в автоматизированных системах управления Развитие теории и практики автоматизированных систем управления (АСУ) связано с выявлением предельных возможностей систем и построением систем, наилучших (оптимальных) по какому-либо критерию. В качестве критерия оптимальности АСУ могут быть приняты различные технические, экономические, технико-экономические показатели и оценки. Например, он может отражать технико-экономическую выгоду (производительность, КПД, прибыль и т.п.), при этом оптимизация должна обеспечить максимум критерия оптимальности; может выражать также потери (расход энергии, топлива, средств и т.п.), в этом случае оптимизация должна обеспечить его минимум. Проектирование систем должно осуществляться комплексно, на основе системного подхода к оптимизации процесса автоматизированного управления [1]. При оптимизации автоматизированных систем инженер должен быть способен количественно оценить требуемое качество системы, сформулировав цели оптимизации, которые математически выражаются как требования обеспечения экстремальных значений критериев оптимальности в общем случае являющихся функционалами [2]. При создании автоматизированных систем рассматриваются задачи оптимизации режимов с учетом ограничений, определяемых условиями работы объекта управления, для детерминированных и случайных сигналов как при неизменных, так и при изменяющихся параметрах и характеристиках объекта управления и сигналов внешних воздействий. Качество функционирования АСУ характеризуется широким спектром различных функционалов, в зависимости от конкретных задач, объектов управления и условий их эксплуатации. В АСУ, относящихся по функционально-алгоритмическому признаку к системам оптимального управления, решение задачи оптимизации осуществляется на основании получаемой от управляемого объекта информации и принятых математических моделей. Такими системами, например, являются системы прямого многосвязного цифрового управления с оптимизацией, системы управления последовательными технологическими операциями, связанными по качеству, системы адаптивного управления технологическими комплексами. Выработка регулирующих воздействий или советов лицу, принимающему решения, производится в реальном времени. При решении задач об оптимизации систем управления в динамике, сформулированных так, что управления и переменные состояния объекта управления не достигают ограничений, используются методы классического вариационного исчисления. 1. Критерии оптимальности автоматизированных систем управления При проектировании и оптимизации АСУ важным моментом является формулировка цели оптимизации, которая математически выражается как требование обеспечения экстремального значения некоторого критерия оптимальности. Оптимизация автоматизированных систем управления предприятиями (АСУП), служит для совершенствования управления производством и повышения его эффективности. АСУ технологическими процессами (АСУ ТП) составляют основу современного производства и созданы в связи с его большими объемами и сложностью. Существенными принципами построения АСУ являются: системный подход, рассмотрение их как больших систем с многоуровневой иерархической структурой и разработка на основе принципов оптимальности и адаптации. При этом решение задачи управления на базе модели всего предприятия встречает значительные трудности, обусловленные большой размерностью модели и высокой степенью неопределенности возмущающих воздействий. Эти трудности преодолеваются путем перехода к рассмотрению многоуровневой иерархической модели. В общем случае АСУП можно рассматривать как иерархическую систему, в которой функции управления распределены по уровням следующим образом: оптимальное планирование; оперативное управление; оптимизация процессов; оптимизация режимов установки. Подсистемы управления первых двух уровней решают задачи управления предприятием в целом, т. е. административно-хозяйственные задачи (распределение запасов, оперативный учет, планирование, анализ деятельности предприятия за длительное время, оптимизация графиков планово-предупредительного ремонта и т.п.). Это автоматизированные системы, для которых характерно присутствие человека в качестве элемента управляющей системы. Выбор критерия эффективности при решении задач оптимизации на этих уровнях определяется экономическими требованиями. Управление на третьем и четвертом уровнях осуществляется с помощью автоматических систем. При этом системы управления третьего уровня иерархии могут быть многомерными и относиться к классу больших систем. Управляемые технологические процессы могут быть элементарными и сложными. Элементарные процессы ведутся в отдельных аппаратах, агрегатах. Число управляющих переменных в таких процессах мало, критерий оптимальности представляет собой некоторый технологический показатель. Для проведения сложных процессов требуется технический комплекс, образованный совокупностью аппаратов и агрегатов. При большом числе переменных, характеризующих сложный процесс, критерий оптимальности носит экономический характер. К четвертому уровню относятся локальные системы управления, предназначенные для поддержания определенных на третьем уровне оптимальных режимов установок и агрегатов. Высокая точность ведения процессов приводит к экономии энергетических и материальных ресурсов, более эффективному использованию средств автоматизации. Это в свою очередь сказывается на снижении затрат, а следовательно, уменьшении себестоимости продукции, повышении производительности труда и эффективности производства в целом. Системы управления каждой иерархической ступени выполняют свои функции в рамках установленных производственных и технологических ограничений; в то же время они связаны между собой как общими материальными и энергетическими потоками, так и общими назначением и целью всего производственного цикла. Каждая система различных иерархических уровней имеет свою цель, задаваемую извне системой более высокого ранга. Качество процесса достижения этой цели обычно характеризуется показателем эффективности управления. Основными критериями качества автоматических систем являются: стоимость разработки, изготовления и эксплуатации систем; качество функционирования; надежность; потребляемая энергия; масса; объем и т. п. Каждый из этих частных критериев является некоторой функцией нескольких переменных, характеризующих систему в целом. При разработке простейших локальных систем управления обычно рассматривают задачу оптимизации по критериям, характеризующим качество функционирования системы (точность и быстродействие), а остальные частные критерии не учитывают. В зависимости от конкретных условий функционирования систем обычно рассматривают две задачи оптимизации режимов: статических и динамических. Задача динамической оптимизации ставится для подсистем нижнего уровня, статической – характерна для верхних уровней управления. В теории автоматического управления широко распространены функционалы, характеризующие качество функционирования системы. В общем случае функционал зависит от координат состояния, управления и возмущающих воздействий и может быть представлен как
где [t0, tk] — рассматриваемый интервал времени; G(...) — функция, отражающая показатель качества; X, U, F — векторы координат состояний, управлений и возмущений соответственно. Достижение максимального (или минимального) значения этого функционала указывает на оптимальное поведение или состояние системы. Критерии типа (1) называют скалярными, если они представляют только один частный критерий из совокупности всех критериев, характеризующих качество автоматических систем. При этом наиболее часто рассматривают задачи обеспечения минимума отклонений X и U во время переходного процесса при единичном входном воздействии или возмущении F, минимума времени переходного процесса и минимума среднеквадратичной ошибки. В задачах обнаружения сигналов, где важно знать не величину ошибки, а лишь факт ее наличия или отсутствия, приходится пользоваться другими критериями оптимальности, например критериями минимума вероятности ошибочного решения, условного минимума вероятности ошибочного решения, минимума среднего риска и др. В зависимости от принадлежности к переходному или установившемуся режиму работы объектов и системы управления сложными процессами применяются следующие типы критериев оптимальности. В качестве показателя качества может приниматься время переходного процесса:
Полученная при этом система является оптимальной по быстродействию, если обеспечивается минимум критерия (2) с учетом ограничений координат. В качестве критерия оптимальности могут быть применены известные в теории автоматического управления интегральные оценки качества переходного процесса. Так , например, при использовании квадратичной интегральной оценки система будет оптимальной, если обеспечивается минимум интеграла
где ε(t)=yзад–y(t) – отклонение выходной переменной у(t) от заданного значения yзад. Полученная при этом система является оптимальной по точности в динамических режимах при отработке ненулевых начальных условий или единичном задающем воздействии. В общем случае может быть использована обобщенная интегральная оценка, когда рассматривается отклонение не только выходной переменной у(t), но и ее производных. Критерий оптимальности (3) может быть использован для оценки качества адаптации системы в условиях неопределенности. В качестве критериев оптимальности автоматических систем при случайных сигналах может быть использовано среднее значение квадрата ошибки системы 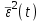 или среднее значение квадрата выходной координаты или среднее значение квадрата выходной координаты 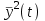 : :
где ε(t) и y(t) – случайные процессы ошибки и выходной координаты. Полученная при этом система является оптимальной по точности в статистическом смысле, если обеспечивается минимум интегралов (4) или (5). В качестве критериев оптимальности системы при возмущающих воздействиях fв(t) могут быть приняты функционалы, характеризующие взаимную корреляцию между координатами выхода y(t) и возмущения fв(t):
Полученная при этом система является оптимальной по точности в динамике при возмущениях fв(t), если обеспечивается минимум интегралов (6) и (7). При управлении от источников энергии, ограниченных по мощности, используется частный критерий в виде функционала, характеризующего расход энергии на управление. Например, для электрического источника энергии:
где u(t) и i(t) – напряжение и ток нагрузки источника; r= 1/R – коэффициент пропорциональности, R – сопротивление электрической цепи. Полученная из условия минимума функционала (8) система является оптимальной по расходу энергии на управление. Функционал типа (8) характеризует стоимость управления в ряде случаев, когда u(t) – координата управления, а r – весовой коэффициент. В механических системах для оценки энергии управления иногда принимают функционал вида
где u(t) – координата управления; 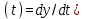 – производная выходной переменной объекта. – производная выходной переменной объекта.В качестве критерия оптимальности, характеризующего расход топлива, используется функционал
Полученная из условия минимума функционала (10) система является оптимальной по расходу топлива. В более общей постановке задачи синтеза оптимального управления вместо (1) минимизируемый функционал для детерминированных и стохастических объектов может быть записан соответственно как
где Gk– функция, характеризующая качество в конечный момент времени tk. При оптимизации статики и установившихся режимов многомерных объектов обычно ставится задача получения минимума или максимума функций многих переменных, характеризующей качество в статических или установившихся |режимах работы объекта:
где Q(...) – функция, характеризующая показатель качества; xi – переменные, определяющие режим работы объекта. Полученная при этом система является оптимальной в установившихся режимах. В частном случае функция Q(X) может быть нелинейной статической характеристикой многомерного объекта. Управление технологическим процессом состоит в поиске и реализации технологических режимов, обеспечивающих наилучшее соотношение между количественными и качественными показателями процесса при минимуме производственных затрат. Математическое описание технологических процессов на оперативных интервалах принимается неизменным и обычно представляется в виде нелинейных (в общем случае) регрессионных зависимостей, связывающих количественные и качественные показатели выходных продуктов с количественными и качественными показателями потоков на входе и управляющими воздействиями Ui. При статической оптимизации технологического процесса в качестве критерия оптимальности может быть принята функция пользы:
где Хвх – вектор входных переменных технологического процесса; Y – вектор переменных выхода; U – вектор управляющих воздействий. В качестве критерия оптимальности сложных систем управления может быть принят критерий максимума прибыли (чистого дохода) технологического процесса
где qj – цена j-го продукта; Пj – производительность процесса по j-му целевому продукту; S – затраты. Критерий максимума прибыли технологического процесса не всегда согласуется с глобальным критерием производства. Это обстоятельство ограничивает его использование в качестве основного скалярного критерия на низших уровнях оптимизации. Если скорость протекания технологических процессов такова, что переменные процесса на рассматриваемом интервале времени нельзя считать постоянными, то функция пользы (13) будет зависеть от времени. В таких случаях в качестве критерия оптимальности принимается либо усредненная функция пользы
где Т – оперативный интервал управления, либо функция пользы в конечный момент времени. Оптимизация технологических процессов может быть также выполнена в соответствии с критерием минимума потерь
где n – число реализуемых переменных технологического процесса; xi – i-я реализуемая переменная процесса; Si – стоимость потерь от нестабильности i-й переменной ( 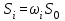 , причем , причем 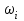 – весовые коэффициенты ( – весовые коэффициенты (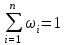 ); Sо – общие потери от колебаний стабилизируемых переменных в локальных системах регулирования технологического процесса). ); Sо – общие потери от колебаний стабилизируемых переменных в локальных системах регулирования технологического процесса).В некоторых случаях оптимизации статики технологических процессов критерий оптимальности может быть выражен в виде функции многих переменных типа (12). Если скорость протекания технологического процесса такова, что критерий оптимальности типа (12) нельзя считать неизменным во времени, то необходимо оптимизировать технологический процесс в динамике, используя функционал, например, вида
В случаях, когда необходимо обеспечить наилучшую работу системы в наихудших возможных условиях, применяют критерий оптимальности, называемый минимаксным. Встречаются также типы задач по определению оптимальных решений, когда имеются две стороны, интересы которых противоположны и каждая сторона стремится получить максимальную выгоду для себя. Эти задачи являются предметом теории игр. Формирование критерия оптимальности, определяющего цель оптимиза-ции, – это инженерная и инженерно-экономическая задача, которая решается на основе всестороннего изучения управляемого объекта. В общем случае качество автоматических систем может быть определено несколькими критериями. Иногда можно ограничиться выбором одного частного критерия, принимаемого в качестве основного, важнейшего для данной задачи оптимизации. Если необходимо учесть различные показатели качества автоматической системы, то задача выбора критерия оптимальности существенно усложняется, так как требования, предъявляемые к системе, обычно оказываются противоречивыми. Например, желательно всегда иметь максимально надежную (частный критерий J1), простую по конструкции (частный критерий J2), дешевую по стоимости (частный критерий J3) систему, потребляющую мало энергии на управление (частный критерий J4), и хорошо функционирующую (частный критерий J5). Среди этих критериев противоречивыми являются, например, критерии J1, J2 и J3. В связи с этим обычно при оптимизации автоматизированных систем в виде основного принимают критерий качества функционирования. Чтобы улучшить АСУ по другим частным критериям, необходимо их также учитывать при постановке задачи оптимизации. Процессы в сложных системах можно достаточно полно оценить только совокупностью различных показателей качества, поэтому для их оптимизации необходимо выбирать несколько частных критериев, характеризующих векторный критерий 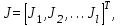 где l – число частных критериев. где l – число частных критериев.В некоторых случаях можно заменить векторный критерий эквивалентным обобщенным скалярным критерием оптимальности. Если частные критерии независимы друг от друга, и можно оценить выгоду от каждого частного критерия Jj в одних и тех же единицах измерения (например, денежных), то вместо векторного критерия можно применить обобщенный скалярный критерий, определяемый функционалом
где cj(Jj) – функция, выражающая стоимость выигрыша от значения критерия Jj. В частном случае стоимость выигрыша может быть пропорциональной критерию Jj, т. е. 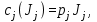 где pj – коэффициенты пропорциональности. где pj – коэффициенты пропорциональности.Тогда вместо (18) получим обобщенный функционал в виде суммы частных критериев
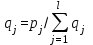 – весовые коэффициенты. – весовые коэффициенты.Функционалы вида (19) позволяют свести задачу оптимизации по векторному критерию к эквивалентной задаче оптимизации по обобщенному скалярному критерию и для ее решения применить известные методы синтеза оптимальных систем. Например, в задачах оптимизации систем по точности при детерминированных сигналах и расходу энергии на управление применяют функционал (3) частного критерия J1, характеризующего качество функционирования системы, и функционал (8) частного критерия J2, характеризующего расход энергии при управлении. При этом векторный критерий, определяемый совокупностью критериев J1 и J2, имеющий вид
может быть заменен эквивалентным обобщенным скалярным критерием типа (19):
где 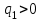 и и 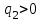 – весовые коэффициенты. – весовые коэффициенты.Если частные критерии Jj многомерных объектов и процессов являются зависимыми и объединить их в один обобщенный скалярный критерий вида (18) или (19) не удается, то при оптимизации таких объектов и процессов принимается векторный критерий. Например, в задачах оптимизации систем по быстродействию и расходу энергии на управление с учетом ограничения сигнала управления необходимо применить векторный критерий, который определяется функционалами (2), (8):
Неудобство применения векторных критериев состоит в том, что при оптимизации объекта управления требуется выполнять сложные многоэтапные решения задачи максимизации (или минимизации) каждого частного функционала. В связи с этим на практике обычно ограничиваются решением задачи оптимизации по какому-либо одному частному критерию. В задачах оптимизации объектов по быстродействию, например, вместо векторного критерия (22) применяют критерий типа (2), в результате чего стоимость управления не минимизируется. Таким образом, основу оптимизационных задач составляет формализация представления о качестве функционирования систем управления. Подобная формализация предполагает, прежде всего, построение количественных характеристик качества функционирования, величины которых зависят от принимаемых проектных решений. Такими характеристиками могут служить различные функционалы, характеризующие качество процессов в АСУ, учитывая наиболее важные требования, предъявляемые к системе. Задачи оптимизации системы управления в динамике при выбранном критерии качества в виде функционала (1), имеющие ограничения в виде математической модели динамики объекта управления могут быть решены методами классического вариационного исчисления. |

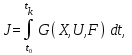

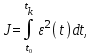

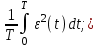
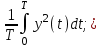
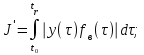
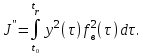
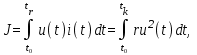
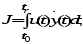
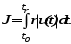 .
.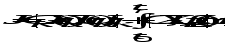

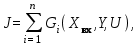
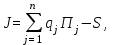




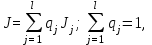
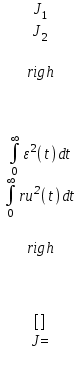
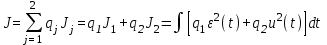 ,
,