Ориентированные графы курсовая. Курсовая_Зебольд. Ориентированные графы

• Название: Ориентированные графы
• Анкор: Ориентированные графы курсовая
• Дата: 12.01.2023
• Размер: 70.53 Kb.
• Имя файла: Курсовая_Зебольд.docx
• Тип: Курсовая; #882839

МИНИСТЕРСТВО НАУКИ И Высшего ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФГАОУ ВО «СЕВЕРО-КАВКАЗСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

Факультет математики и компьютерных наук имени профессора Н.И. Червякова

КАФЕДРА вычислительной математики и кибернетики


КУРСОВАЯ РАБОТА
по дисциплине

«Дискретная математика»

на тему:

«Ориентированные графы»
Выполнил:

Зебольд Даниил Александрович

студент 2 курса

группы ПМИ-б-о-21-1

направления 01.03.02 – Прикладная математика и информатика

Направленность (профиль) Вычислительная математика и математическое моделирование

очной формы обучения

________________________

(подпись)
Руководитель работы:

Самойленко В.В.

доцент кафедры Вычислительной математики и кибернетики

Работа допущена к защите _______________________ ______________

(подпись руководителя) (дата)
Работа выполнена и

защищена с оценкой _________________________ Дата защиты______________
Члены комиссии: ________________ __________ _______________

(должность) (подпись) (И.О. Фамилия)

________________ _______________ _______________

(должность) (подпись) (И.О. Фамилия)

________________ _______________ _______________

(должность) (подпись) (И.О. Фамилия)
Ставрополь, 2022 г.

Содержание
Введение 3

1. Ориентированные графы 4

1.1 Основные определения 4

1.2 Полустепени исхода и полустепени захода 8

1.3 Пути 11

2. Описание алгоритма 15

3. Описание программы 17

3.1. Общие сведения 17

3.2. Функциональное назначение 17

3.3. Описание логической структуры программы 17

3.4. Использование технических средств 18

3.5. Описание данных 18

3.6. Руководство пользователю 18

3.7. Структурная схема программы 19

Заключение 20

Список литературы 21

Введение

В настоящее время дискретная математика и смежные с ней разделы привлекают большое внимание специалистов различных областей науки и техники, являясь эффективным аппаратом формализации современных инженерных задач, связанных с дискретными объектами. Особое значение с практической точки зрения имеет теория графов, использующаяся при проектировании интегральных схем и схем управления, исследовании автоматов и логических цепей, при системном анализе, автоматизированном управлении производством, при разработке вычислительных и информационных сетей, в схемотехническом и конструкторско-топологическом проектировании, и т.д. Обширное применение теория графов находит в современной вычислительной технике и кибернетике: в теоретическом программировании, при проектировании ЭВМ, баз данных, систем логического управления.

В приложениях часто приходится рассматривать гра­фы с ориентированными ребрами, т. е. ребрами, для ко­торых указаны начало и конец. Примерами таких графов являются сети автомобильных дорог с односторонним дви­жением или схемы программ для ЭВМ. Недостаточно простых (неориентированных) графов и для описания несимметричных отношений. Примерами подобных отно­шений могут служить порядок выполнения комплекса ра­бот, задаваемый с помощью сетевого графика, или тур­нирная ситуация в спортивных соревнованиях.

Темой курсовой работы является поиск сильных компонент ориентированного графа. Работа состоит из трех частей: в первой, теоретической, будет дан обзор основных понятий для ориентированных графов; во второй – приведен алгоритм поиска сильных компонент; в третьей – программная реализация алгоритма и описание программы.

1. Ориентированные графы

1.1 Основные определения

Пусть V — конечное непустое множество, V² — его де­картов квадрат. Ориентированный граф (орграф)—это па­ра (V, А), где A  V². Элементы множества V называют­ся вершинами орграфа G=(V, А), а элементы множества А — его дугами. Таким образом, дуга — это упорядочен­ная пара вершин. Множества вершин и дуг орграфа G обозначаются через VG и AG соответственно. Число |VG| называется порядком орграфа G и обозначается через |G|.

Если х = (u, v) — дуга, то вершины u и v называются ее концевыми вершинами, причем u называется началом дуги х, а. v — концом. Говорят, что дуга инцидентна каж­дой из своих концевых вершин. Говорят также, что дуга исходит из своего начала и заходит в свой конец. Дуга с совпадающими началом и концом, т. е. дуга вида (v, v), называется петлей. Можно определить ориентированные графы с несколькими дугами, имеющими общее начало и общий конец (мультиграфы). Такие дуги называются параллельными.

На рисунке дуга изображается направленной линией, идущей от начала дуги к концу. Направление линии обозначается стрелкой. Например, для графа G, представленного на рис. 1, VG={v₁, v₂, v₃, v₄, v₅}, AG= {x₁, x₂, x₃, x₄, x₅, x₆, x₇}, причем x₁ и x₂ —параллель­ные дуги, a x₇ — петля.

Вершины орграфа называются смежными, если они являются концевыми для некоторой дуги. Дуги называ­ются смежными, если они имеют общую концевую вершину.

Пусть G— некоторый орграф. Ориентированным марш­рутом (или просто маршрутом) в графе G называется такая последовательность

S = (v₀, x₁, v₁, x₂, v₂, x₃, v₃, x₄,.., v_n, x_n,) (1)

его чередующихся вершин v_i и дуг х_j, что x_i = (v_i-1, v_i) (i = 1, n). Такой маршрут назо­вем (v₀, v_n) – маршрутом. Вер­шины v₀ и v_n назовем крайни­ми, а остальные вершины маршрута (1) — промежуточны­ми (внутренними). Длиной маршрута называется число входящих в пего дуг. Маршрут называется цепью, если все входящие в пего дуги различны, и путем, если все входящие в него вершины, кроме, возможно, крайних, различны.

Если в орграфе G нет параллельных дуг, то маршрут (1) может быть задан последовательностью входящих в него вершин: S=( v₀, v₁, v₂, v₃,.., v_n). В любом случае марш­рут можно задать последовательностью входящих в него дуг: S = (x₁, x₂, x₃, x₄,.., x_n,)

Рис. 1.
Маршрут называется циклическим, если его первая и последняя вершины совпадают. Циклический путь назы­вается контуром. Очевидно, что любой (u, v) – маршрут при u  v содержит (u, v)-путь, а при u = v — контур.

Последовательность (1) чередующихся вершин и дуг орграфа G, таких что x_i = (v_i-1, v_i) или x_i = (v_i, v_i-1), на­зывается полумаршрутом. Аналогично определяются по­луцепь, полупуть и полуконтур.

Если в орграфе существует (u, v) -маршрут, то гово­рят, что вершина v достижима из вершины u. Любая вер­шина считается достижимой из себя самой.

Орграф называется сильным (или силъносвязным), если любые две его вершины достижимы друг из друга. Орграф называется односторонним (или односторонне-связным), если для любой пары его вершин по меньшей мере одна достижима из другой. Орграф называется сла­бым (слабосвязным, связным), если любые две его вер­шины соединены полупутем.

Поскольку любая вершина графа достижима из себя, то одновершинный граф одновременно и сильный, и одно­сторонний, и слабый.

Очевидно, что каждый сильный граф является одно­сторонним, а каждый односторонний — слабым. Очевидно также, что любые две несовпадающие вершины сильного орграфа принадлежат некоторому циклическому маршруту.

На рис. 2, а изображен сильный орграф, на рис. 2, б — односторонний, а на рис. 2, в — слабый.

Рис. 2.
Маршрут, содержащий все вершины орграфа G, на­зывается остовным.

Утверждение 1. Орграф является сильным тогда и только тогда, когда в нем есть остовный цикличе­ский маршрут.

 Необходимость. Пусть G — сильный орграф и T = (v₀, x₁, v₁, x₂, v₂,.., x_n, v₀)—его циклический маршрут, проходящий через максимально возможное число вершин. Если этот маршрут не является остовным, то возьмем вне его вершину v. Так как G — сильный орграф, то сущест­вуют маршруты

T₁ = (v₀, y₁, .., v), T₂ = (v₀, z₁, .., v₀)

Но тогда циклический маршрут

T’ = (v₀, x₁, v₁, .., x_n, v₀, y₁, .., v, .., z₁, v₀)

содержит большее, чем Т, число вершин, что противоре­чит выбору маршрута Т. Следовательно, Т — остовный маршрут.

Достаточность. Пусть u и v — две произвольные вершины орграфа G, а

T = (v₀, x, .., v, y, .., v, .., z,.., v₀)

— циклический маршрут. Тогда u достижима из v с по­мощью маршрута (v, у, ..., u)—части маршрута Т, — а v из u — с помощью маршрута (u, z, ..., v₀, х, ..., v).

Аналогично доказывается

Утверждение 2. Орграф является односторон­ним тогда и только тогда, когда в нем есть остовный маршрут. Орграф является слабым тогда и только тогда, когда в нем есть остовный полумаршрут.

Подграфы и порожденные подграфы ориентированного графа определяются так же, как и для неориентиро­ванного. Так же определяются и операции над оргра­фами.

Введем важное понятие сильной компоненты орграфа. Сильной (или силъносвязной) компонентой ориентирован­ного графа называется любой его максимальный относи­тельно включения сильный подграф.

Очевидно, что отношение взаимной достижимости вер­шин ориентированного графа G рефлексивно, симметрич­но и транзитивно. Следовательно, мы получим разбиение множества VG на классы, объединив в один класс все вершины, достижимые друг из друга. Подграфы, порож­денные классами этого разбиения, и только они, служат сильными компонентами орграфа G.


Рис. 3.
В орграфе могут быть дуги, не входящие ни в одну из его сильных компонент.

Орграф G, изображенный на рис. 3, имеет четыре сильные компоненты с множествами вершин {v₁, v₂, v₃, v₄}, {v₅, v₆, v₈}, {v₇} и {v₉}.

Пусть {S₁, S₂, ..., S_m} — множество всех сильных ком­понент ориентированного графа G. Конденсацией орграфа G называется орграф G*, вершины s₁, s₂, ..., s_m которого соответствуют сильным компонентам орграфа G, и пара (s_i, s_j) является дугой в G* тогда и только тогда, когда в G есть дуга, начало которой принадлежит компоненте S_i а конец — S_j.

На рис. 3 представлены орграф G и его конденса­ция G*.

Утверждение 3. Конденсация G* любого оргра­фа G не имеет контуров.

 Проведем доказательство от противного. Пусть Т = (s₀, x₁, s₁, …, s₀) — контур в G*. Тогда каждая вер­шина, входящая в компоненту S_i, достижима из любой вершины, входящей в компоненту S_j. Но это противоречит максимальности сильных компонент.

Неориентированный мультиграф, получающийся в ре­зультате снятия ориентации с дуг орграфа G, называется основанием орграфа G и обозначается через G_b.

Очевидно, что орграф является слабым тогда и только тогда, когда его основание — связный мультиграф.

Орграф называется несвязным, если его основание — несвязный мультиграф.

Ориентированный граф называется турниром, если его основание является полным графом. Этот класс графов получил свое название в связи со спортивными турнира­ми без ничьих, проводимыми по круговой системе. Резуль­таты встреч можно описать ориентированным графом, вершины которого соответствуют участникам соревнова­ний, а дуга (u, v) есть в орграфе, если участник u побе­дил участника v.

1.2 Полустепени исхода и полустепени захода

Пусть G — ориентированный граф и v  VG. Множе­ство концов всех дуг, исходящих из вершины v, обозна­чается через Г(v), а множество начал всех дуг, заходя­щих в v — Г^-1(v).

.Полустепенью исхода d⁺(v) вершины v называется число дуг, исходящих из v, т. е. d⁺(v) = |Г(v)|. Анало­гично определяется полустепень захода d^-(v) вершины v:

d^-(v) = |Г^-l(v)|.

Степень deg v вершины v орграфа — это число инци­дентных ей дуг:

deg v = d⁺(v) +d^-(v)

Для произвольной бинарной m*n – матрицы А вектор c_A = (c₁, c₂, …, c_m), i-я координата с_i, которого равна чис­лу единиц в i-й строке этой матрицы, называется векто­ром строчных сумм. Аналогично определяется вектор столбцовых сумм d_A = (d₁, d₂, …, d_n): координата d_i равна числу единиц в i-м столбце. Очевидно, что

(2)

поскольку каждая из этих сумм равна числу всех единиц матрицы А.

Если А = А(G) — матрица смежности орграфа G, то



т. е. число единиц в i - й строке матрицы A(G) равно по­лустепени исхода i- й вершины, а число единиц в j - м столбце равно полустепени захода j-й вершины. Таким образом, для A =A(G) имеем

c_A = (d⁺(1), d⁺(2), …, d⁺(n))

d_A = (d^-(1), d^-(2), …, d^-(n))

Поэтому верно следующее утверждение, являющееся ана­логом леммы о рукопожатиях.

Утверждение 4. Сумма полустепеней исхода всех вершин орграфа равна сумме полустепеней захода и равна числу его дуг:



Нетрудно убедиться в том, что равенство (2) не явля­ется достаточным условием для существования бинарной n*m – матрицы А с векторами строчных сумм с_A и столб­цовых сумм d_A. Например, нет матрицы А, для которой с_A = (3, 0), d_A = (2, 1).

Пара векторов c = (c₁, c₂, …, c_m), d = (d₁, d₂, …, d_n) с целыми неотрицательными координатами называется графической, если существует бинарная m*n – матрица А, для которой с_А = с, d_А = d. Если истолковывать эту мат­рицу как приведенную матрицу смежности двудольного графа, то вектор с_А окажется списком степеней вершин этого графа, принадлежащих одной доле, а вектор d_А — списком степеней вершин другой доли, так что условия графичности пары векторов являются условиями сущест­вования соответствующего двудольного графа — реализа­ции этой пары. Этим и объясняется термин «графическая пара векторов».

При m = n ту же матрицу А можно истолковывать как матрицу смежности орграфа, и тогда условия графично­сти пары векторов станут условиями существования ори­ентированного графа с заданными списками полустепеней исхода и полустепеней захода вершин.

Критерий графичности пары векторов устанавливается следующей теоремой.

Теорема 5. Пара векторов

c = (c₁, c₂, …, c_m), d = (d₁, d₂, …, d_n) (3)

является графической тогда и только тогда, когда выпол­няются следующие два условия:

1) последовательность

(c₁+m-1, c₂+m-1, …, c_m+m-1, d₁, d₂, …, d_n) (4)

графическая;

2)

 Очевидно, что пара векторов (3) реализуется дву­дольным графом тогда и только тогда, когда последова­тельность (4) реализуется расщепляемым графом, для которого (c₁+m-1, c₂+m-1, …, c_m+m-1) и (d₁, d₂, …, d_n) — списки степеней вершин верхней и ниж­ней долей соответственно. Поэтому доказываемое непо­средственно вытекает из критерия расщепляемости гра­фической последовательности.

Коснемся вопроса о реконструируемости орграфов. Ги­потезу Келли — Улама для ориентированных графов мож­но попытаться сформулировать так же, как и для неори­ентированных. Но для орграфов эта гипотеза не верна.

П. Стокмейер (1977, 1981 гг.) нашел несколько семейств нереконструируемых орграфов. Одно из них состоит из сильных турниров специального вида. Два нереконструи­руемых турнира изображены на рис. 4. Ф. Харари и Е. Палмер доказали (1967 г.), что любой турнир, не яв­ляющийся сильным, реконструируем.


Рис. 4.
А. Рамачандран предложил новый вариант гипотезы реконструируемости для орграфов. Пусть G — ориентиро­ванный граф. Вместе с каждым подграфом G_v = G — v, v  VG, будем рассматривать упорядоченную пару (d⁺(v), d^-(v)) полустепеней исхода и захода вершины v. Орграф G назовем N-реконструируемым, если он опреде­ляется с точностью до изоморфизма набором {(G_v, d⁺(v), d^-(v)): v  VG}.

Гипотеза Рамачандрана (1981 г.). Любой орграф N-реконструируем.

Эта гипотеза пока не доказана и не опровергнута.

1.3 Пути

Пусть

М = (P₁, P₂,…, P_i) (5)

— какое-либо множество путей орграфа G, попарно не имеющих общих вершин. Если множества VP_i вершин этих путей составляют разбиение для VG, т. е.

VG = VP₁  VP₂  ...  VP_i,

то множество путей М называется разбиением орграфа G на пути. Минимальное число l путей, составляющих раз­биение орграфа G, обозначим через l(G).

Ниже фигурируют понятия числа независимости ₀(G) и хроматического числа (G) орграфа G, которые для ориентированных графов определяются так же, как и для неориентированных, т. е. ₀(G) = ₀(G_b), (G) =  (G_b).

Теорема 6. Для любого орграфа G верно неравенство l(G)  ₀(G)

Фиксируем некоторое разбиение (2) орграфа G на пу­ти. Пусть N(M) = (a₁, a₂, …, a_i), a_i  Р_i — множество на­чальных вершин этих путей. Докажем более сильное ут­верждение:

существует такое разбиение М' орграфа G на пути, что

N(M’)  N(M), |M’|  ₀(G)

Доказательство последнего утверждения проведем индукцией по n = |G|. Утверждение очевидно при n = 1, 2. Пусть n > 2 и утверждение верно для орграфов, порядки которых меньше n.

Вначале покажем, что, не ограничивая общности, мож­но считать |М|  ₀(G)+1. В самом деле, пусть |М|  ₀(G)+2. Рассмотрим орграф G₁ = G —VP₁. Очевид­но, что ₀(G₁) . ₀(G). По индуктивному предположе­нию существует разбиение М₁ орграфа G₁ на пути с N(M₁)  N(M) и |М₁|  ₀(G₁)  ₀(G). Но тогда М' = M₁  P₁ — разбиение орграфа G с N(M')N(M) и |М’|  ₀(G)+1. Поэтому всегда можно считать, что |М|  ₀(G)+1.

Пусть теперь |М| = ₀(G)+1. Тогда множество N(M) = (a₁, a₂, …, a_i) не является независимым, т. е. в нем есть хотя бы одна пара смежных вершин. Предполо­жим, что (a₁, a₂)  AG. Если путь P₁ состоит из единст­венной вершины a₁, то объединив P₁ и P₂ в путь (a₁, a₂, …), получим нужное разбиение.

Если же путь Р = (а₁, b₁, ...) имеет более чем одну вершину, то рассмотрим орграф G₁ = G—a₁. По индук­тивному предположению существует такое разбиение M₁ орграфа G₁ на пути, что |М₁|  ₀(G₁)  ₀(G) и N(M₁) = {b₁, a₂, a₃, ..., а_i}. Если b₁  N(M₁), то М' полу­чим из M₁, добавив вершину a₁ к пути, начинающемуся в b₁. Аналогично можно поступить и тогда, когда а₂  N(M₁). Если же b₁  N(M₁) и a₂  N(M₁), то М' = M₁  {(a₁)}.

Из теоремы 6 вытекают два важных следствия.

Орграф G называется транзитивным, если истинна импликация

((x, y) AG и (y, z)  AG)  (x, z)  AG

Следствие 7. Если орграф G транзитивен, то l(G) = ₀(G).

Согласно предыдущей теореме l(G)  ₀(G). Но две вершины транзитивного орграфа, принадлежащие од­ной цепи, смежны, поэтому ₀(G)l(G). Итак, l(G) = ₀(G).

Следствие 8. В каждом турнире существует гамилътонов путь.

Поскольку любые две вершины, произвольного тур­нира Т смежны, то ₀(T)=1. Поэтому существует цепь Р, содержащая все вершины турнира Т.

Для сильных турниров верно следующее более общее утверждение.

Теорема 9. Пусть Т — сильный турнир порядка n. Тогда для любой его вершины u и для любого числа k, 3  k  n, в Т есть контур длины k, содержащий вер­шину u.

Пусть S (u) и Р(u) — множество всех тех вершин v и, соответственно, w турнира Т, для которых (u, v)  AT и (w, u)  АТ. Оба эти множества не являются пу­стыми, поскольку орграф Т сильный. По той же причине существует хотя бы одна дуга (v, w), идущая из S (u) в Р(u) (рис. 5). Следовательно, вершина и лежит на контуре длины 3.

Далее воспользуемся индукцией по k. Пусть вершина u входит в контуры всех длин от 3 до k, где k < n. По­кажем, что она входит в контур длины k + 1.

Пусть С=(v₀, v₁, …, v_k), v₀ = v_k = u, — контур дли­ны k. Предположим, что для некоторой вершины w, не входящей в этот контур, су­ществуют такие дуги (w, x) и (у, w), что x  VC и у  VC. Тогда в С есть такие две смежные вершины v_i, и v_i+1, что (v_i, w) и (w, v_i+1)—ду­ги турнира Т.

Сле­довательно, вершина u вхо­дит в контур

С=(v₀, v₁, …, v_i, w, v_i+1, …, v_k)

v₀ = v_k = u

длины k + 1.

Рис. 5.
Если же указанной выше вершины w нет, то множе­ство вершин турнира Т, не входящих в контур С, можно разбить на две части S (С) и Р(С) так, чтобы для любых вершин aS(C), bP(C) и v  С выполнялись усло­вия (v, а)  AG и (b, v)  AG. Так как орграф T сильный, то S(С) и Р(С) не пусты и существует дуга, идущая из некоторой вершины a  S(С) в некоторую вершину b  Р(С) (рис. 6). Таким образом, вершина u входит в контур

С‘ = (v₀, a, b, v₂, …, v_k)

длины k + 1.

Очевидно

Следствие 10. Сильный турнир гамильтонов. Заметим, что предыдущее следствие вытекает также из теоремы 9.

Теорема 11. Если k—максимальная длина путей в орграфе G, то (G).k + 1.

Обозначим через В такое минимальное относительно включения подмножество в АG, что орграф G₁ = G — В не имеет контуров. Для любой вершины v определим t(v) как число вершин пути в орграфе G₁ с началом в v, имею­щем максимальную длину. Приписав каждой вершине v цвет t(v), получим раскраску орграфа G не более чем k + 1 цветами. Остается доказать, что эта раскраска пра­вильная, т. е. что t(u)  t(v) для любых двух смежных вершин u и v. Но если (u, v)  АG₁, то t(u)>t{v). Если же (u, v)  В, то G₁+(u,v) имеет контур. Поэтому в G₁ существует (v, u) - путь и, следовательно, t(v)>t(u).

Итак, доказано, (G).k + 1.

Рис. 6.

2. Описание алгоритма

Матрицей достижимости графа с n вершинами называется квадратная матрица R порядка n, элементы которой определяются следующим образом:



Матрицей контрдостижимости графа с n вершинами называется квадратная матрица Q порядка n, элементы которой определяются следующим образом:





Матрицей сильной связности орграфа с n вершинами называется квадратная матрица S порядка n, элементы которой определяются следующим образом:



При машинной реализации алгоритмов на графах матрицы расстояний, достижимости, контрдостижимости и сильной связности можно определять через матрицу смежности.

Пусть дан граф G, - его матрица смежности. Элементы матрицы расстояний D можно вычислить при машинной реализации следующим образом: d_ij равно наименьшему из чисел n, для которых a_ijⁿ > 0, где a_ijⁿ - элемент матрицы Aⁿ и равно бесконечности, если таких чисел нет.

Пример. Дан граф G (рис. 7). Найти матрицу расстояний D.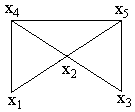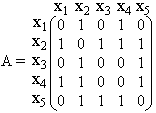


Рис. 7

Сначала найдем матрицу смежности A, элемент a_ij которой равен 1, если вершины x_i и x_j графа G смежны, и равен нулю в противном случае. В матрице D диагональные элементы будут равны нулю, так как расстояние между вершинами x_i и x_j, если i = j, считается равным нулю. Если элемент a_ij матрицы A равен 1, то соответствующий элемент d_ij матрицы D тоже будет равен 1. Недоопределенная матрица D изображена ниже.

Умножим матрицу А саму на себя по правилу умножения матриц и найдем матрицу A².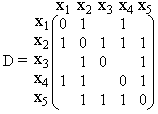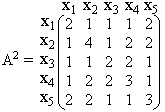



Так как в матрице A² нет нулевых элементов, то оставшиеся неопределёнными элементы матрицы D равны 2. Окончательно матрица D будет иметь вид: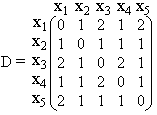



Матрицу достижимости R можно найти с помощью матрицы смежности А следующим образом R = T(E+A+A²+...+A^n-1), где n  число вершин, E  единичная матрица, а оператор T определяется следующим образом:



Матрица контрдостижимости Q находится транспонированием матрицы достижимости R: Q = R^T.

Последовательность определения сильных компонент.

1. Построение матриц достижимости R и контрдостижимости .

2. Определение матриц .

3. Выделение сильных компонент графа. Вершины, соответствующие одинаковым строкам и столбцам матрицы S, принадлежат одной сильной компоненте графа.

3. Описание программы

3.1. Общие сведения

Программа написана на языке Turbo Pascal версии 7.0 Отладка производилась в операционной системе MS Windows 95 на компьютере совместимом с IBM PC с процессором 80486 DX4.

3.2. Функциональное назначение

Программа предназначена для определения сильных компонент ориентированного графа. Максимальное число вершин обрабатываемого графа может быть не более 15. Ввод матрицы графа осуществляется из текстового файла с именем STRONG. Вывод результатов расчета производится на экран.

3.3. Описание логической структуры программы

Константы.

Nmax = 15 - максимальное число вершин обрабатываемого графа.

Типы:

Link = ^PLink - тип - список.

PLink = record - тип запись с полями:

sled - ссылочное поле - связь со следующим элементом.

P - признак наличия пути: 1 - есть, 0 - нет.

Mat2 - двумерный массив максимальной размерностью 15 * 15 состоящий из 0 и 1.

Mas1 - одномерный массив максимальной размерностью 15 с элементами от 0 до 15.

MasMno - массив максимальной размерностью 15 с элементами типа множество 1..15.

Переменные (основные).

G - матрица смежности исходного графа;

R - матрица достижимости;

Q - матрица контрдостижимости;

C - произведение Адамара;

C1 - матрица С, приведенная к блочно - диагональному виду.

SetOfStr - массив множества сильных компонент;

Описание процедур

1) Процедура Dostig

Составление матрицы достижимости графа.

2) Процедура BDG

Формирует блочно - диагональную матрицу.

3) Процедура Silnie

Нахождение сильных компонент графа.

3.4. Использование технических средств

Для использования программы необходимы следующие условия:

Требования к компьютеру. Для нормальной работы программы требуется любой IBM - совместимый компьютер с процессором 80386 или выше с минимальной конфигурацией: оперативная память не менее 1024 Кбайт, размер свободного дискового пространства не менее 50 Кбайт для размещения основной программы, цветной графический монитор EGA, VGA, SVGA.

Программное обеспечение. Разработка и отладка программы производилась с использованием интегрированной среды Turbo Pascal 7.0.

Программа может работать в операционной системе MS-DOS не ниже пятой версии.

3.5. Описание данных

Входные данные:

 матрица смежности графа, расположенная в текстовом файле с именем STRONG. Каждая строка этого файла представляет собой набор из 0 и 1, разделенных одним пробелом.

 число вершин графа – определяется программно при считывании матрицы смежности.

Выходные данные:

 количество сильных компонент графа;

 список вершин для каждой компоненты.

3.6. Руководство пользователю

Запуск программы производится выбором из панели Norton Commander файла с именем SILNYE.EXE и нажатия клавиши Enter.

После этого работа с программой производится без вмешательства пользователя в следующей последовательности:

- чтение данных их текстового файла с именем STRONG;

- преобразование списка и формированием матрицы смежности графа;

- формирование матриц достижимости, контрдостижимости и произведения Адамара;

- приведение матрицы Адамара к блочно - диагональному виду;

- поиск сильных компонент графа;

- вывод решения.

3.7. Структурная схема программы

Начало

Чтение данных из файла
Вывод матрицы смежности
Формирование матрицы достижимости Dostig и расчет произведения Адамара

Приведение к блочно – диагональному виду BDV
Поиск сильных компонент Silnie
Вывод сильных компонент
Конец

Заключение

Главным итогом выполнения курсовой работы было создание программы определения сильных компонент ориентированного графа в соответствии с поставленной задачей и получение практических результатов работы программы. Созданная программа позволяет:

- ввод размерности исходной матрицы смежности графа из файла;

- формировать решение в соответствии с условием поставленной задачи;

- вывод на экран исходного графа и полученных компонент.

Созданная программа полностью удовлетворяет поставленной задаче, но при этом имеет ряд недостатков:

- нет вывода на печать результатов расчета;

- нет контроля правильности вводимых данных;

- ограниченная размерность графа.

Доработка указанных недостатков позволит сделать программу более универсальной и надежной.

Список литературы

1. Бондарев В.М. Основы программирования. Харьков: Фолио, 1997, 367 с.

2. Лекции по теории графов / Емеличев В.А., Мельников О.И., Сарванов В.И., Тышкевич Р.И. -М.: Наука, 1990, 384 с.

3. Нефедов В.Н., Осипова В.А. Курс дискретной математики / Учебное пособие. -М:. МАИ, 1992 г. -264 с.

4. Фаронов В.В. Программирование на персональных ЭВМ в среде ТУРБО - ПАСКАЛЬ. -М., изд - во МГТУ, -1991, -580 с.

5. Фаронов В.В. Turbo Pascal 7.0. Начальный курс. -М.: Нолидж, -1997, 616 с.