термодинамика. Основы химической термодинамики
 Скачать 1.12 Mb. Скачать 1.12 Mb.
|
|
Свойства энтропии Зависимость энтропии от объема Рассмотрим, как изменится энтропия одного моля газа при изменении объема системы. Вместо отношения термодинамических вероятностей подставим соответствующую зависимость (3.7) для 1 моля газа: 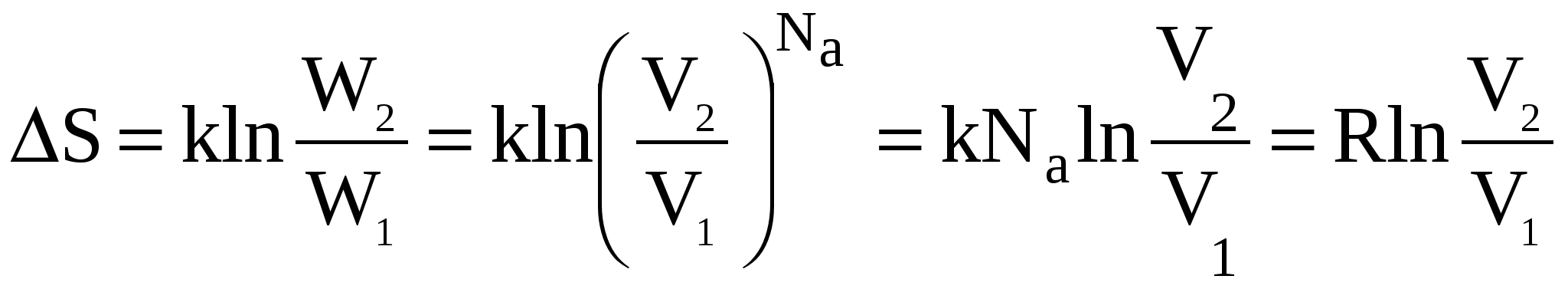 (10) (10)R = 8,31 Дж/моль Из этого уравнения следует, что процессы, сопровождающиеся увеличением объема системы при сохранении числа молекул, участвующих в процессе, протекают с увеличением энтропии системы. Зависимость энтропии от давления Из уравнения состояния идеального газа следует, что для 1 моля газа: Подставляя это выражение в уравнение (3.9), получим для изотермического (протекающего при постоянной температуре) процесса: При увеличении давления энтропия системы уменьшается. Если давление выразить в атмосферах, атмосферное давление обозначить ро (напомним, что ро = 1, а энтропию при этом давленииSo, то получим: или энтропия
Следует обратить внимание, что в уравнении (13) р выражено в абсолютных атмосферах. Если в условиях задачи давление дается в атмосферах избыточных, необходимо перевести его в абсолютные: рабс. = ризб. +1. Полученная зависимость (13) характерна только для газовой фазы, на энтропию конденсированных (твердых, жидких) систем изменение давления практически не оказывает влияние, а влияют такие факторы, как тип кристаллической решетки, прочность связей и т.д. Так, величины энтропии твердого фосфора значительно различаются в зависимости от типа кристаллической решетки («белая» или «красная» модификация): Sо298,Р(бел) = 41,09 Дж/моль·К; Sо298,Р(кр) = 22,8 Дж/моль·К. Зависимость энтропии от температуры С повышением температуры энтропия возрастает. Действительно температура повышается за счет подвода теплоты (по мерее увеличения температуры становится возможным все большее число состояний, так как молекулы могут переходить в состояние со все более высокими значениями энергии, что приводит к увеличению термодинамической вероятности), 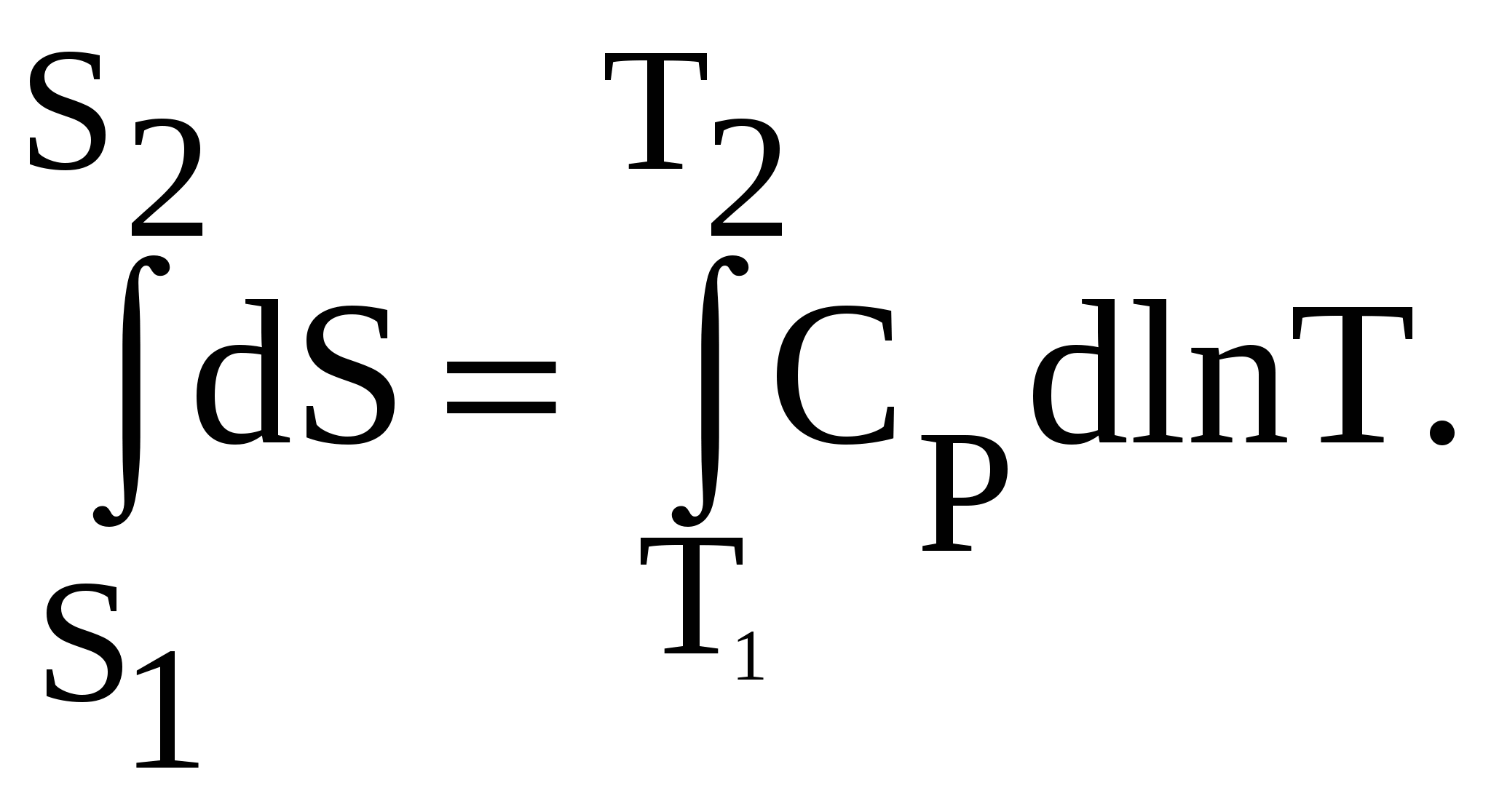 (14) (14)Интегрируя это уравнение, получаем следующее выражение: На рис. 4. показан характер зависимости энтропии вещества от температуры. Как видно из рисунка 4, при фазовом переходе (ф.п.) вещества (из твердого состояния в жидкое, из жидкого в газообразное состояние) энтропия вещества скачкообразно возрастает, что связано с переходом в состояние с большей неупорядоченностью. Изменение энтропии вещества при любых фазовых переходах (ф.п.) равно:
Зависимость энтропии вещества от температуры при постоянстве фазового состава определяется уравнением (14а). В интервале умеренных температур (300 - 500К) этим изменением при ориентировочных расчетах часто пренебрегают. Уравнение температурной зависимости энтропии 1 моля вещества в пределах одного фазового состояния: где Ср – мольная теплоемкость при р = const. 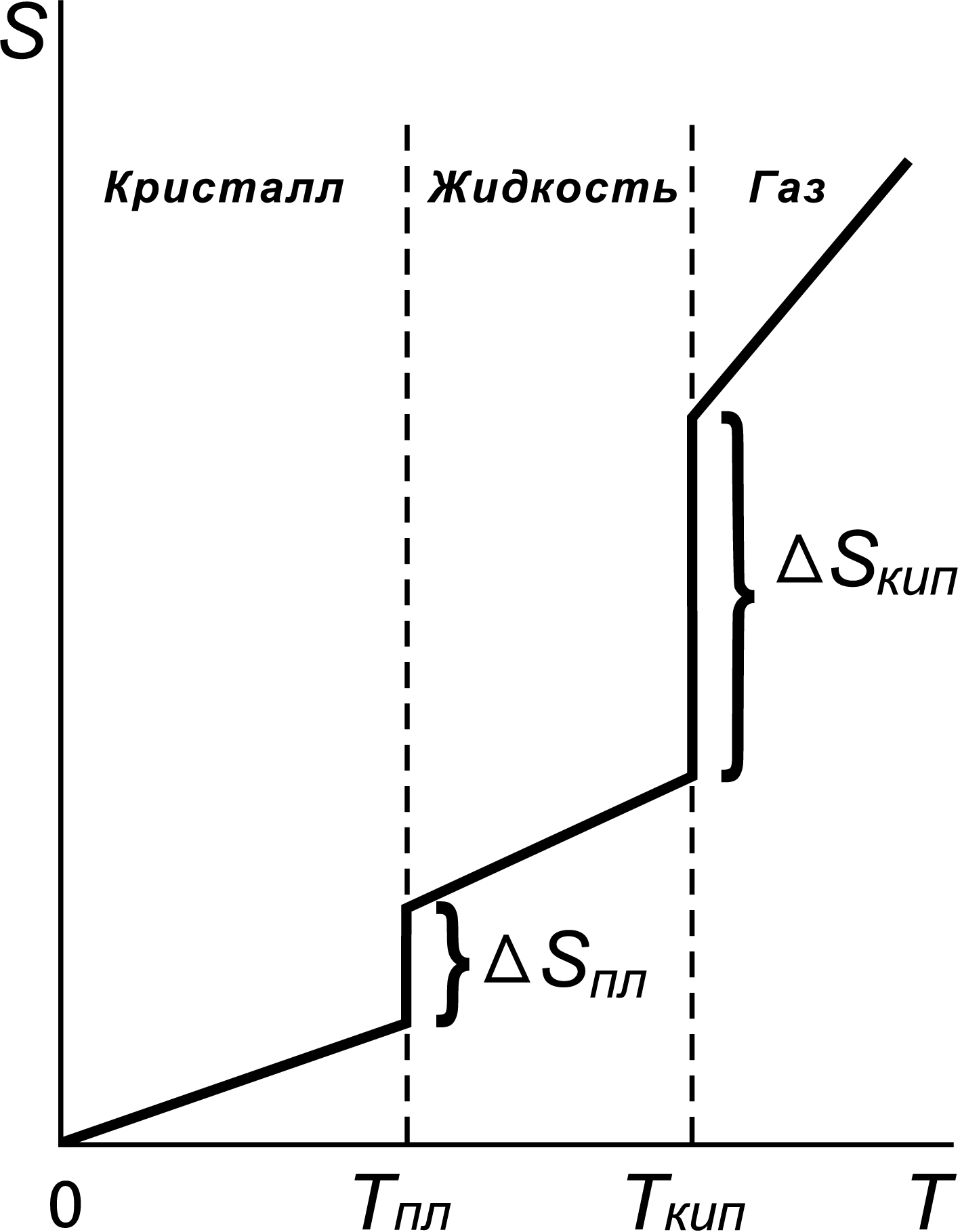 Рис. 4. Зависимость энтропии вещества от температуры. Принимая Ср = const в интервале температур Т1 и Т2 получаем Обратите внимание, что зависимость на рис.4 выходит из начала координат. При температуре равной абсолютному нулю тепловое движение отсутствует, все атомы в идеальном кристалле занимают строго определенные места в пространстве. Такое состояние системы может быть реализовано единственным способом, поэтому при этом W = 1, а S = 0. Это третий закон термодинамики, называемый также постулатом Планка. Энергия Гиббса и состояние химического равновесия Для реакции АВ(г) А(г) + В(г) энтропийно выгодным будет процесс распада АВ(г) на компоненты Учитывает эти противоположные тенденции предложенная американским физико - химиком Д. Гиббсом функция состояния, которая называется энергией Гиббса:
В этом уравнении произведение энтропии и температуры (TS) определяет величину “связанной” энергии, т.е. ту часть энергии (энтальпии) системы, которую невозможно перевести в работу. Тогда разница между «энергосодержанием» системы (Н) и «связанной» энергией дает долю энергии, которую можно в принципе перевести в работу. Таким образом, энергия Гиббса определяет работоспособность системы. При обратимом и изотермическом проведении процесса G равно по абсолютной величине, но обратно по знаку максимальной полезной работе (Аmax), которую система может произвести в данном процессе: GР = - Аmax. Использование энергии Гиббса позволяет однозначно определить направление самопроизвольных процессов, происходящих в системе. Возможен только самопроизвольный переход системы из состояния с большей энергией Гиббса в состояние с меньшей энергией Гиббса. Это другая, более общая формулировка второго закона термодинамики). Таким образом, критерием самопроизвольного протекания процесса при изобарно-изотермических условиях является неравенство GР 0, справедливое для любых систем. В любой самопроизвольной реакции происходит превращение исходных веществ, имеющих некоторую величину энергии Гиббса, в продукты, имеющие меньшую ее величину. Заметим, что полученный ранее критерий для изолированных систем S 0 является частным случаем: эти системы не обмениваются энергией с окружающей средой, поэтому для них H = 0 и G 0, только тогда, когда S 0. Если при переходе из одного состояния в другое энтропия системы не изменяется (S = 0), то фактором, определяющим направление реакции, будет изменение энтальпии: уменьшение энтальпии (H 0) соответствует уменьшению энергии Гиббса (G 0). В этом случае протекает реакция, идущая с выделением теплоты. Для любых реакций из уравнения G = H - TS следует: 1) если H 0 и S 0, то всегда G 0, т.е. реакция с выделением теплоты и увеличением степени беспорядка возможна при любой температуре; 2) если H 0 и S 0, то всегда G 0, т.е. реакция с поглощением теплоты и увеличением степени порядка невозможна ни при каких условиях; Во всех остальных случаях (H 0, S 0 и H 0, S 0) знак G зависит от соотношения членов H и TS. 3) если H 0, S 0; в этом случае G 0 при 4) если H 0, S 0; тогда G 0 при 5) при равенстве G=0 в системе устанавливается термодинамическое равновесие, которое может смещаться в любую сторону при изменении внешних факторов (температура, давление, концентрации реагирующих веществ). Знак G указывает на направление реакции. При G 0 реакция протекает в прямом направлении, при G 0 возможен лишь обратный процесс. При G = 0 все вещества находятся в химическом равновесии и внешне незаметно никаких изменений и процессов в системе. При фазовых переходах исходя из этого, получается уравнение: 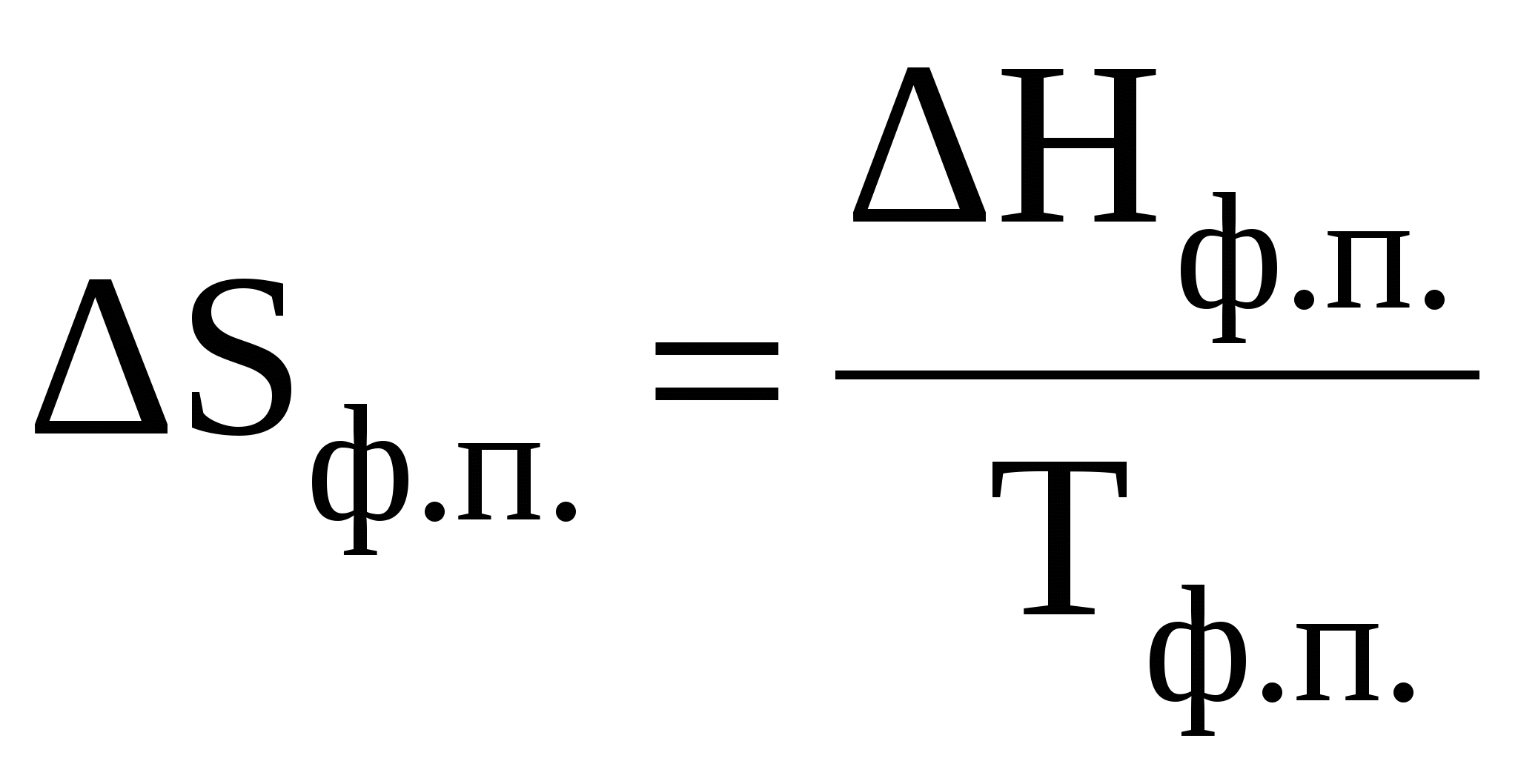 . . Величина энергии Гиббса вещества зависит как от природы этого вещества, так и от его количества. В соответствии с уравнением (18) при условиях отличных от стандартных, при парциальном давлении вещества А равном рА (рА Величина Так как то для n молей вещества А получим: GA = (GoA + RTlnpA)nA, (20) где GA – энергия Гиббса образования вещества А при его парциальном давлении рА (pА1атм); GoA - энергия Гиббса образования 1 моль вещества А при стандартных условиях (рА = 1 атм и Т = 298 К), это стандартная величина, значения которой сведены в таблицы; nA – число молей вещества А. Стандартная энергия Гиббса образования вещества Gо298 – изменение энергии Гиббса в реакции образования 1моль вещества из простых веществ, находящихся в устойчивых состояниях при стандартных условиях (р = 101,3 кПа и Т = 298 К). Значения Gо298 для некоторых веществ приводятся в справочной литературе, размерность Gо298 – кДж/моль. Стандартные энергии Гиббса образования простых веществ, находящихся в стандартном состоянии в устойчивой модификации, равны нулю. Например, Gо298, Н2(газ) = 0. Энергия Гиббса химических реакций. В изобарно-изотермических условиях (т.е. при постоянных давлении и температуре) изменение энергии Гиббса в реакции аА + bВ = сС + dD запишется как 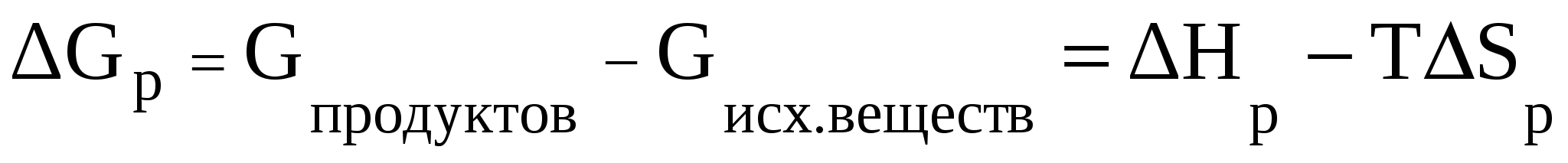 . .В этом уравнении где Изменение энергии Гиббса химической реакции при стандартных условиях (р =101,3 кПа и Т =298 К) можно вычислить по уравнению: Gо298, реакции = Hо 298, реакции – TSо298, реакции , (21) где Hо298,реакции, Sо298,реакции – стандартные изменения энтальпии и энтропии химической реакции, соответственно в кДж и Дж/К; Т - стандартная температура, равная 298 К. Поскольку энергия Гиббса является функцией состояния, то ее значение не зависит от пути протекания процесса, а зависит только от исходного и конечного состояний системы. Изменение энергии Гиббса при стандартных условиях (Gо298, реакции) можно рассчитать, используя стандартные значения энергий Гиббса образования исходных веществ и продуктов реакции с учетом стехиометрических коэффициентов: Gо298, реакции = Изменение энергии Гиббса GТ для реакции, протекающей при температуре, отличной от стандартной (Т GТ = Hореакции – TSореакции. (23) Химическое равновесие Рассмотрим как меняется энергия Гиббса веществ при равновесии химической реакции: аА(Г) Очевидно, что по мере расходования вещества А его энергия Гиббса будет уменьшаться, а энергия Гиббса конечного продукта будет возрастать. При достижении равновесия энергия Гиббса реакции станет равной нулю: Gреакции = Для рассматриваемой реакции: Gреакции = b GB - а GА = 0 или аGА = bGB (24) При равенстве энергий Гиббса продуктов реакции и исходных веществ движущая сила реакции исчерпана, и реакция останавливается, т.е. парциальные давления всех веществ становятся постоянными и не меняются как угодно долго (при данных условиях). Такое состояние химической системы называется состоянием химического равновесия. Установившиеся при этом парциальные давления веществ называются равновесными. Запишем условие равновесия с учетом уравнений (20) и (24): Для нашего случая: 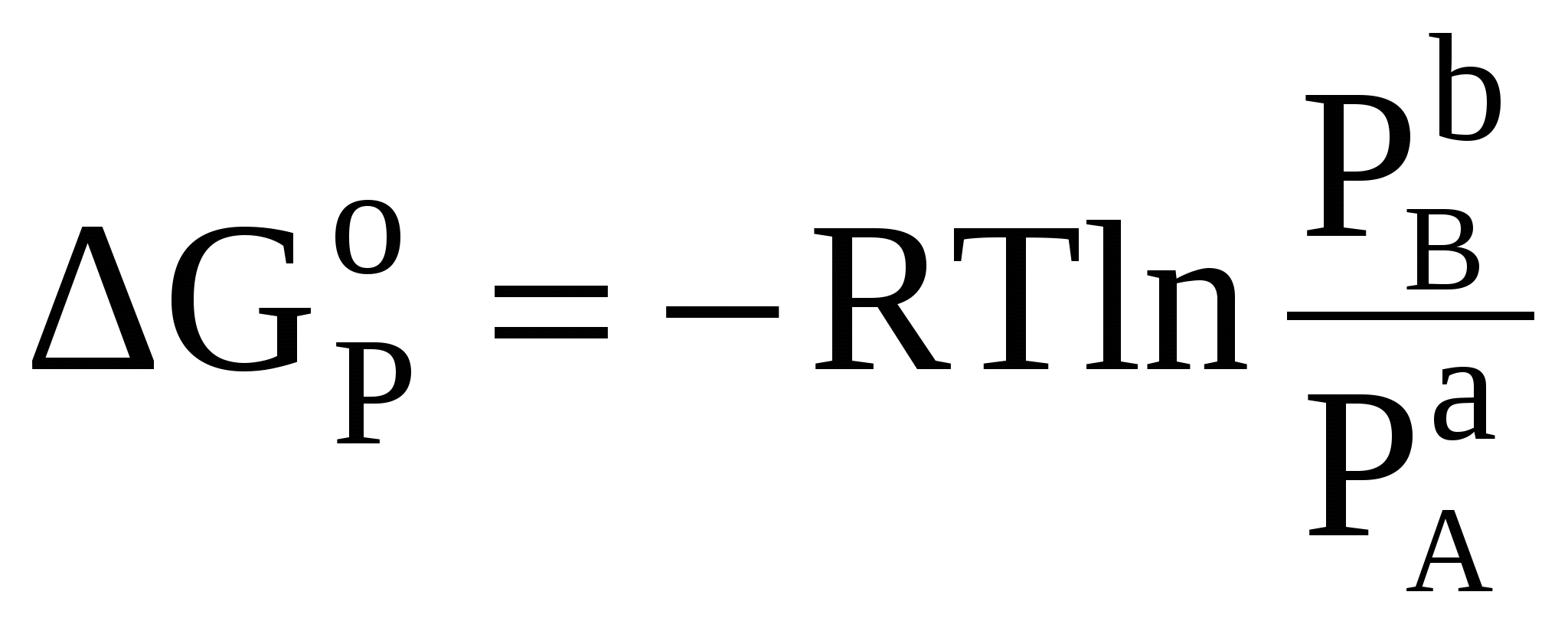 . . Размерность Соотношение равновесных парциальных давлений 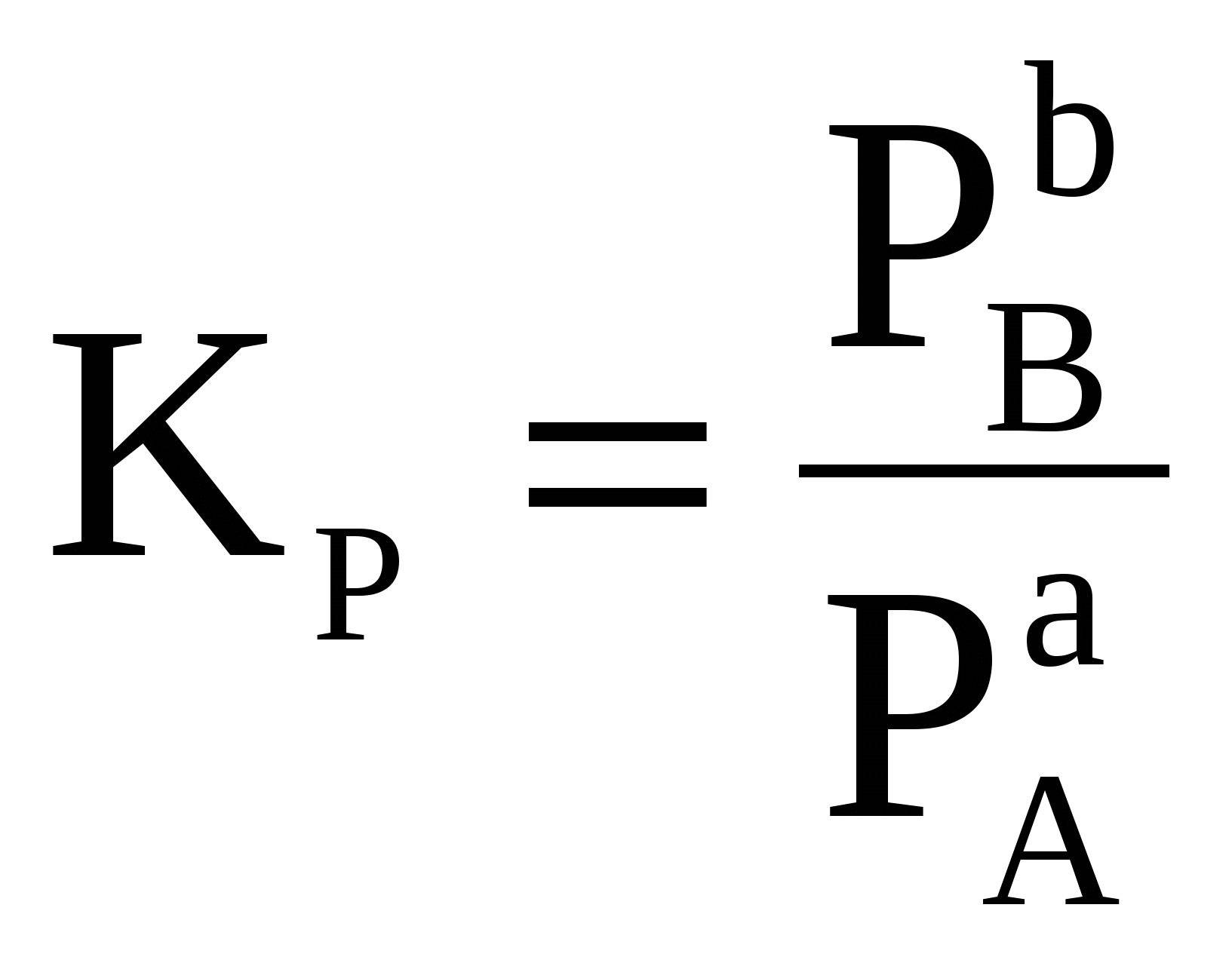 . . Следовательно, можно записать, что: Константа равновесия равна отношению произведения равновесных парциальных давлений продуктов реакции и исходных веществ, возведенных в степени, равные стехиометрическим коэффициентам веществ в рассматриваемой реакции. Например, для реакции N2(Г) + 3H2(Г) « 2 H3(Г) константа равновесия запишется как 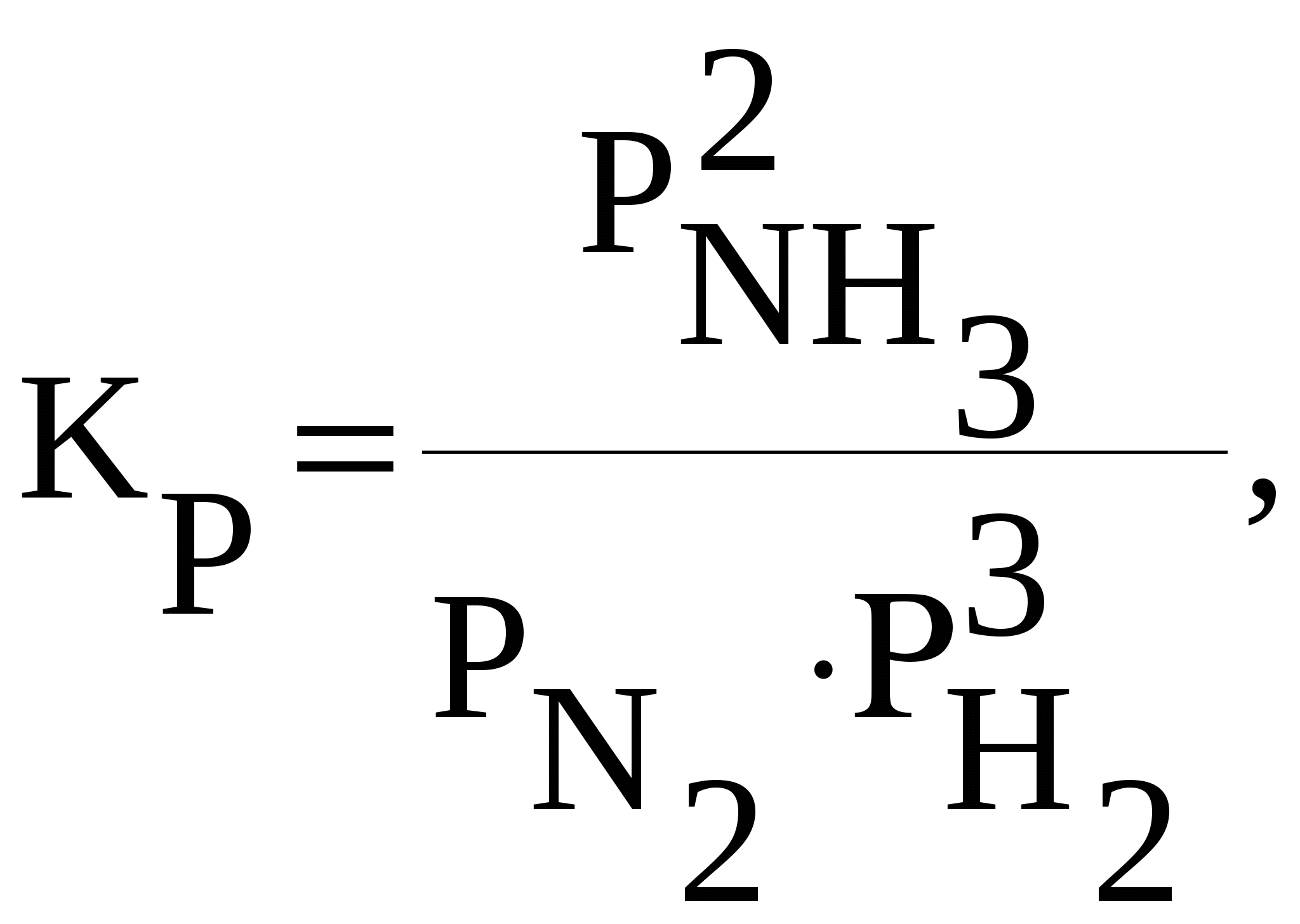 где р – равновесные относительные парциальные давления соответствующих веществ.
КР = КС (RT) ∆v , (27) где R – газовая постоянная, равная 0,082 латм/мольК, если давление выражено в атмосферах, а концентрация в моль/л; ∆ Например, для реакции синтеза аммиака N2(Г) + 3H2(Г) «2 NH3(Г) ∆ Например, для рассмотренной выше реакции константа равновесия запишется как 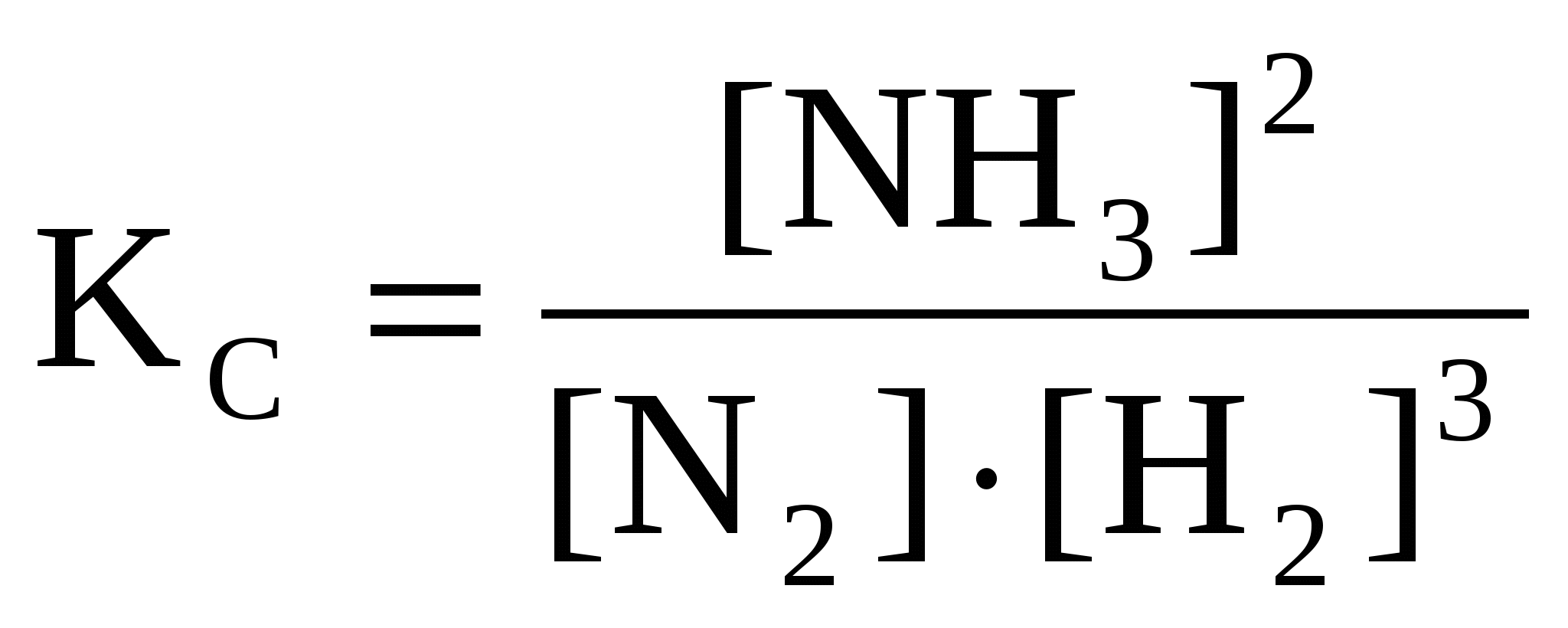 , ,где Если реакция идет без изменения объема (количества молей газообразных веществ в результате реакции не меняется), или реакция протекает в растворе, то КР = КС. Например, для реакции N2(Г) + O2(Г) « 2 NO(Г), КР = КС. Парциальные давления (концентрации) твердых веществ, принимающих участие в реакции, в выражение константы равновесия не включаются. Например, для реакции MgCO3(тв) КР = Л И Т Е Р А Т У Р А 1. Глинка, Н.Л. Общая химия: учеб. / Н.Л. Глинка. – М.: КноРус, 2012. 2. Коровин, Н.В. Общая химия: учеб. / Н.В. Коровин. – изд. Академия, 2011, серия: Высшее профессиональное образование. | ||||||||||||||||||

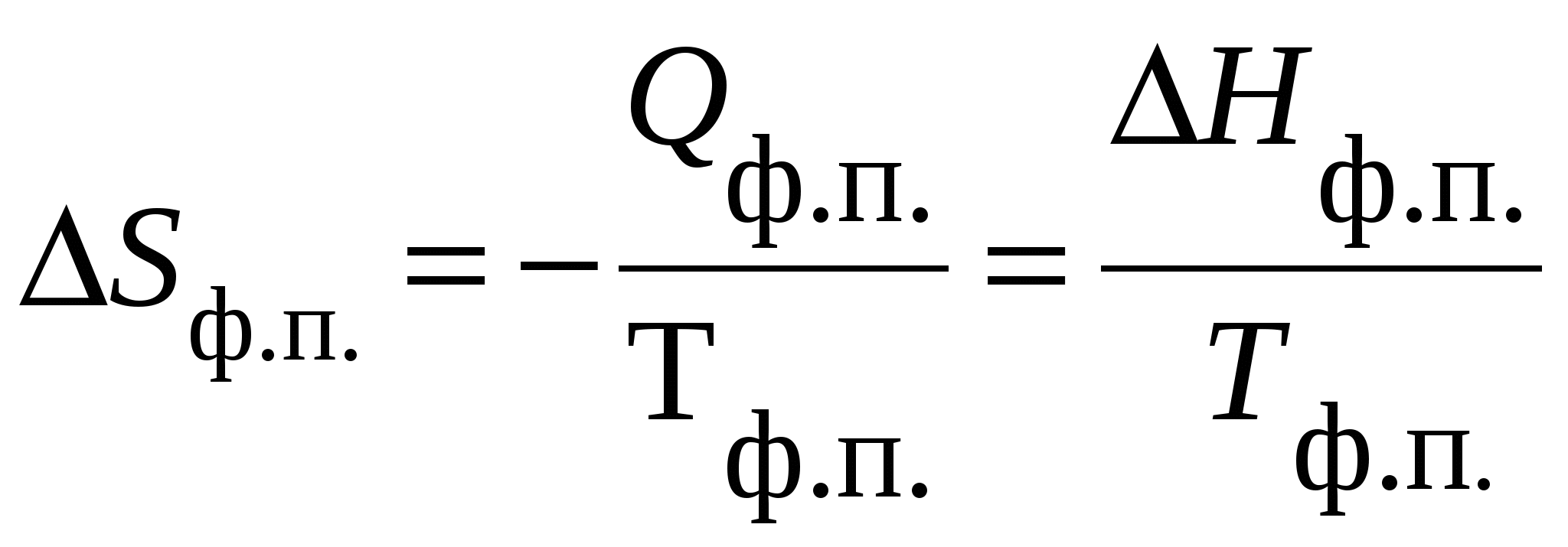 .
.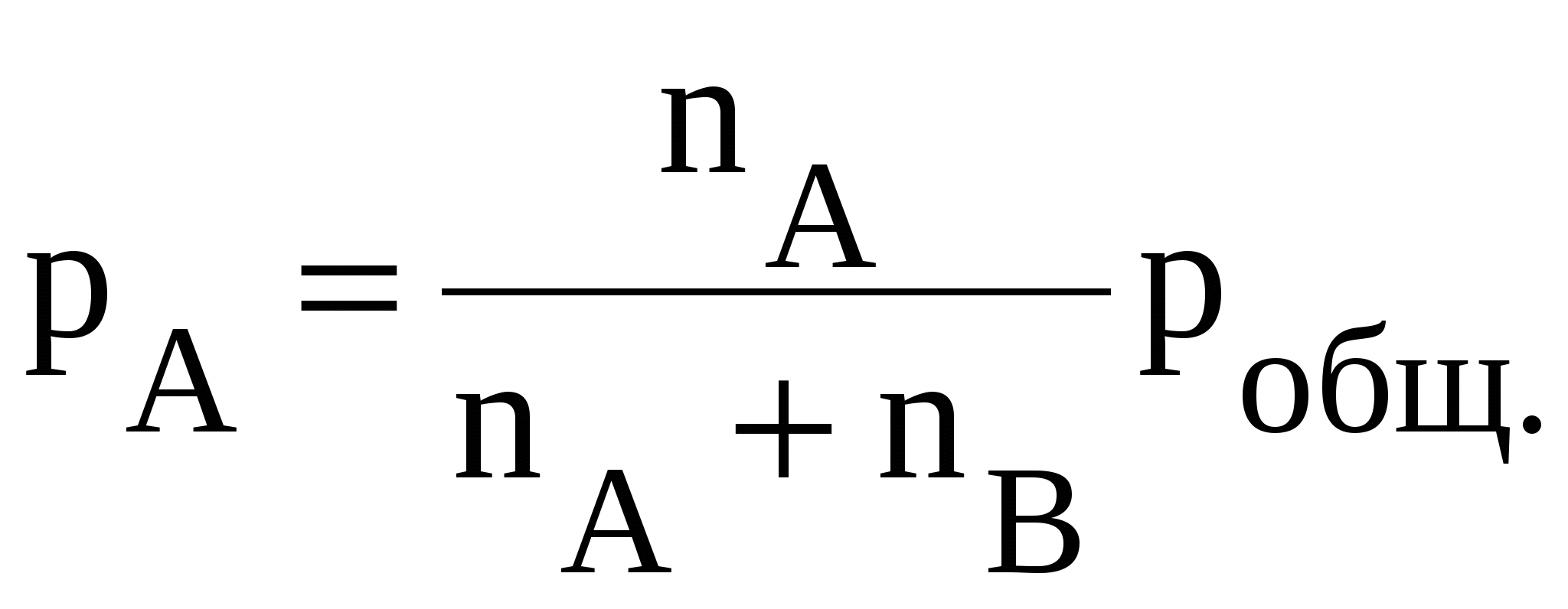 и
и 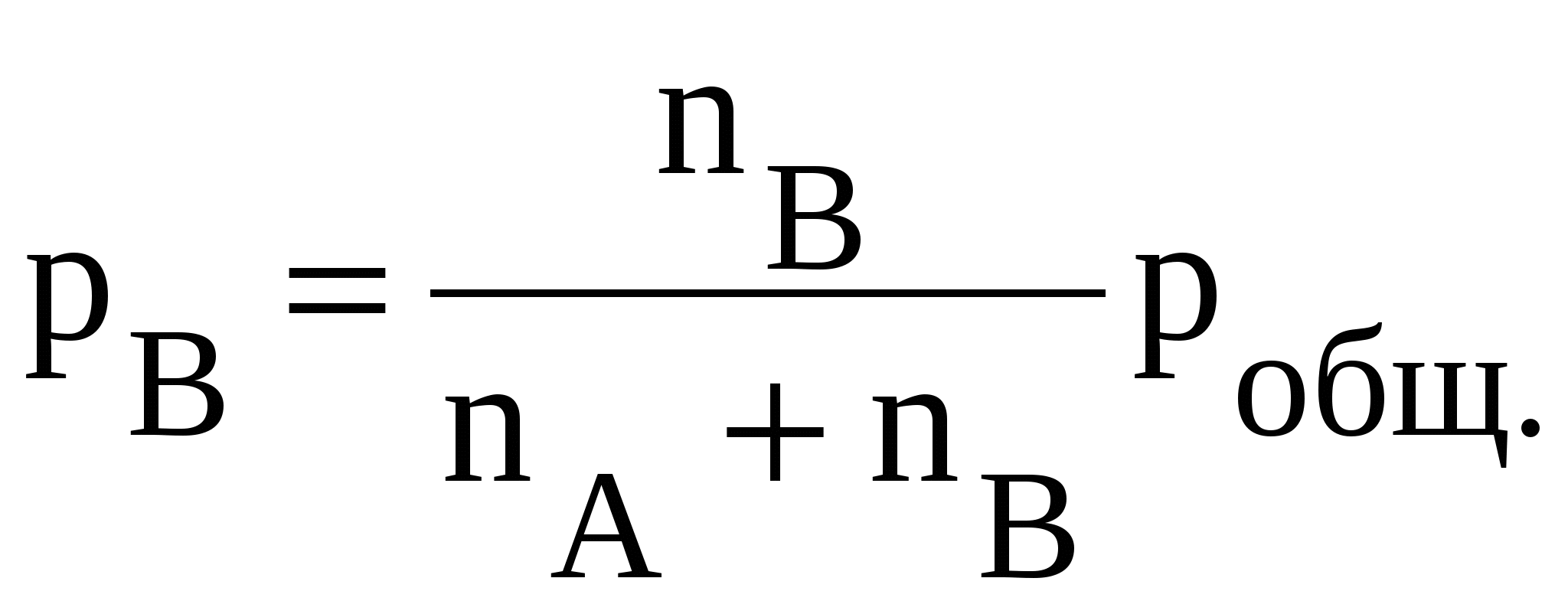 ,
,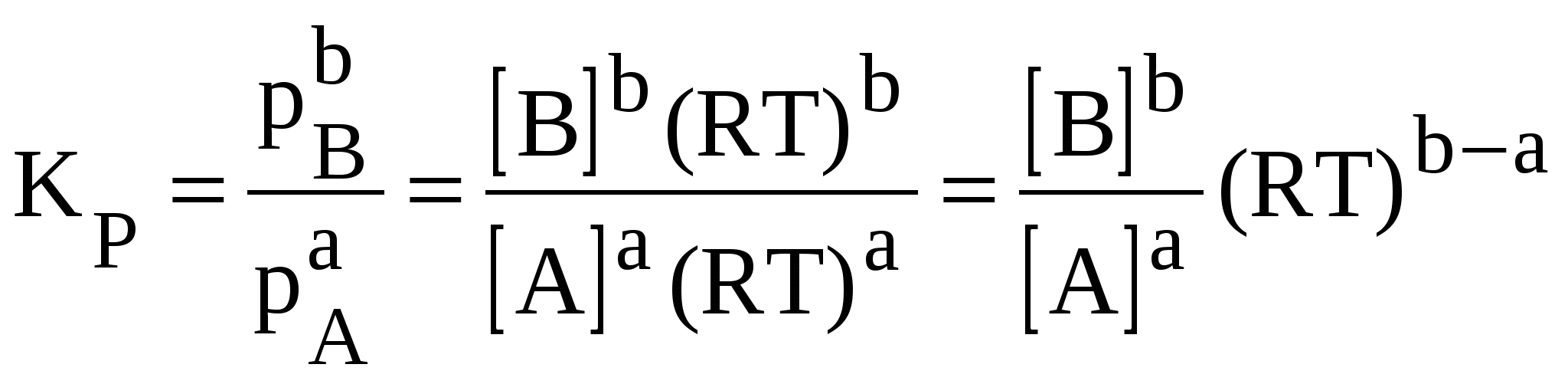 .
.